Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T00:50:03.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Opposing-buoyancy mixed convection through and around arrays of heated cylinders

Published online by Cambridge University Press:  23 September 2022

Tingting Tang ,
Zhiyong Li ,
Shimin Yu ,
Jianhui Li Open the ORCID record for Jianhui Li [Opens in a new window]  and
Peng Yu Open the ORCID record for Peng Yu [Opens in a new window]
Tingting Tang
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China Center for Complex Flows and Soft Matter Research, Southern University of Science and Technology, Shenzhen 518055, PR China
Zhiyong Li
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China Dongguan University of Technology, Dongguan 523808, PR China
Shimin Yu
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China Harbin Institute of Technology, Harbin 150001, PR China
Jianhui Li
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
Peng Yu*
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China Center for Complex Flows and Soft Matter Research, Southern University of Science and Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: yup6@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

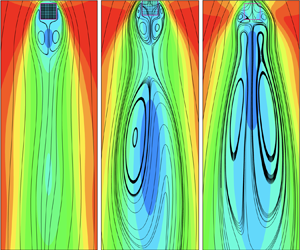
We numerically investigated the opposing-buoyancy mixed convection through and around square arrays of $10\times 10$ heated circular cylinders with the solid fraction ($\phi$) ranging from 0.0079 to 0.66 and the Richardson number ($Ri$) varying from 0 to 1 at a fixed Reynolds number ($Re$) of 100. Our simulations revealed that the large mean recirculation in the far wake can be detached from or connected with the vortex pair in the near wake for different combinations of $Ri$ and $\phi$. Also, it was found that the array with relatively small $\phi$ can significantly promote flow instability even at moderate $Ri$. The instability, which is closely related to the fluctuating heat flux, develops from the lateral sides to the downstream side of the array and gives rise to the large mean recirculation in the far wake. The power spectra density of the array-scale force coefficients demonstrates that the flow undergoes different bifurcation behaviours under various parameter combinations, which reflects the interaction between the near-wake and far-wake vortexes. Interestingly, the Strouhal–Richardson number curves can be collapsed onto the same curve when $Ri$ is increased by a $\phi$-dependent factor. Also, for $\phi \leqslant 0.22$, both the mean drag coefficient and the mean Nusselt number of the array were found to decrease linearly with $Ri$ since the buoyancy within the array becomes prominent in this range of $\phi$.

JFM classification

Convection: Convection in porous media Convection: Buoyancy-driven instability

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A8
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Anirudh, K. & Dhinakaran, S. 2018 On the onset of vortex shedding past a two-dimensional porous square cylinder. J. Wind Engng Ind. Aerodyn. 179, 200–214.CrossRefGoogle Scholar
Badr, H.M. 1984 Laminar combined convection from a horizontal cylinder—parallel and contra flow regimes. Intl J. Heat Mass Transfer 27 (1), 15–27.CrossRefGoogle Scholar
Bharti, R.P., Chhabra, R.P. & Eswaran, V. 2007 A numerical study of the steady forced convection heat transfer from an unconfined circular cylinder. Heat Mass Transfer 43 (7), 639–648.CrossRefGoogle Scholar
Biswas, G. & Sarkar, S. 2009 Effect of thermal buoyancy on vortex shedding past a circular cylinder in cross-flow at low Reynolds numbers. Intl J. Heat Mass Transfer 52 (7–8), 1897–1912.CrossRefGoogle Scholar
Chakkingal, M., de Geus, J., Kenjereš, S., Ataei-Dadavi, I., Tummers, M.J. & Kleijn, C.R. 2020 Assisting and opposing mixed convection with conjugate heat transfer in a differentially heated cavity filled with coarse-grained porous media. Intl Commun. Heat Mass Transfer 111, 104457.CrossRefGoogle Scholar
Chang, K.-S. & Sa, J.-Y. 1990 The effect of buoyancy on vortex shedding in the near wake of a circular cylinder. J. Fluid Mech. 220, 253–266.CrossRefGoogle Scholar
Chatterjee, D. & Mondal, B. 2011 Effect of thermal buoyancy on vortex shedding behind a square cylinder in cross flow at low Reynolds numbers. Intl J. Heat Mass Transfer 54 (25–26), 5262–5274.CrossRefGoogle Scholar
Chatterjee, D. & Ray, S. 2014 Influence of thermal buoyancy on boundary layer separation over a triangular surface. Intl J. Heat Mass Transfer 79, 769–782.CrossRefGoogle Scholar
Dennis, S.C.R. & Chang, G.-Z. 1970 Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42 (3), 471–489.CrossRefGoogle Scholar
Dennis, S.C.R., Hudson, J.D. & Smith, N. 1968 Steady laminar forced convection from a circular cylinder at low Reynolds numbers. Phys. Fluids 11 (5), 933–940.CrossRefGoogle Scholar
Fornarelli, F., Lippolis, A. & Oresta, P. 2017 Buoyancy effect on the flow pattern and the thermal performance of an array of circular cylinders. Trans. ASME J. Heat Transfer 139 (2), 022501.CrossRefGoogle Scholar
Frisch, U. & Kolmogorov, A.N. 1995 Turbulence: the Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Gandikota, G., Amiroudine, S., Chatterjee, D. & Biswas, G. 2010 The effect of aiding/opposing buoyancy on two-dimensional laminar flow across a circular cylinder. Numer. Heat Transfer 58 (5), 385–402.CrossRefGoogle Scholar
Goldman, D. & Jaluria, Y. 1986 Effect of opposing buoyancy on the flow in free and wall jets. J. Fluid Mech. 166, 41–56.CrossRefGoogle Scholar
Guillén, I., Treviño, C. & Martínez-Suástegui, L. 2014 Unsteady laminar mixed convection heat transfer from a horizontal isothermal cylinder in contra-flow: buoyancy and wall proximity effects on the flow response and wake structure. Exp. Therm. Fluid Sci. 52, 30–46.CrossRefGoogle Scholar
Hu, H. & Koochesfahani, M.M. 2011 Thermal effects on the wake of a heated circular cylinder operating in mixed convection regime. J. Fluid Mech. 685, 235–270.CrossRefGoogle Scholar
Issa, R.I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62 (1), 40–65.CrossRefGoogle Scholar
Jafroudi, H. & Yang, H.T. 1986 Steady laminar forced convection from a circular cylinder. J. Comput. Phys. 65 (1), 46–56.CrossRefGoogle Scholar
Ledda, P.G., Siconolfi, L., Viola, F., Camarri, S. & Gallaire, F. 2019 Flow dynamics of a dandelion pappus: a linear stability approach. Phys. Rev. Fluids 4 (7), 071901.CrossRefGoogle Scholar
Liu, S., Jiang, L., Chong, K.L., Zhu, X., Wan, Z.-H., Verzicco, R., Stevens, R.J.A.M., Lohse, D. & Sun, C. 2020 From Rayleigh–Bénard convection to porous-media convection: how porosity affects heat transfer and flow structure. J. Fluid Mech. 895, A18.CrossRefGoogle Scholar
Mahir, N. & Altaç, Z. 2019 Numerical investigation of flow and combined natural-forced convection from an isothermal square cylinder in cross flow. Intl J. Heat Fluid Flow 75, 103–121.CrossRefGoogle Scholar
Makinde, O.D. & Olanrewaju, P.O. 2010 Buoyancy effects on thermal boundary layer over a vertical plate with a convective surface boundary condition. Trans. ASME J. Fluids Engng 132 (4), 044502.CrossRefGoogle Scholar
Morgan, V.T. 1975 The overall convective heat transfer from smooth circular cylinders. In Advances in Heat Transfer (ed. T.F. Irvine & J.P. Hartnett.), vol. 11, pp. 199–264. Elsevier.CrossRefGoogle Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.CrossRefGoogle Scholar
Nield, D.A. & Bejan, A. 2006 Convection in Porous Media, vol. 3. Springer.Google Scholar
Noymer, P.D., Glicksman, L.R. & Devendran, A. 1998 Drag on a permeable cylinder in steady flow at moderate Reynolds numbers. Chem. Engng Sci. 53 (16), 2859–2869.CrossRefGoogle Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.CrossRefGoogle Scholar
Patnaik, B.S.V., Narayana, P.A.A. & Seetharamu, K.N. 1999 Numerical simulation of vortex shedding past a circular cylinder under the influence of buoyancy. Intl J. Heat Mass Transfer 42 (18), 3495–3507.CrossRefGoogle Scholar
Saha, A.K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24 (1), 54–66.CrossRefGoogle Scholar
Salcedo, E., Cajas, J.C., Treviño, C. & Martínez-Suástegui, L. 2017 Numerical investigation of mixed convection heat transfer from two isothermal circular cylinders in tandem arrangement: buoyancy, spacing ratio, and confinement effects. Theor. Comput. Fluid Dyn. 31 (2), 159–187.CrossRefGoogle Scholar
Salimipour, E. 2019 A numerical study on the fluid flow and heat transfer from a horizontal circular cylinder under mixed convection. Intl J. Heat Mass Transfer 131, 365–374.CrossRefGoogle Scholar
Sarkar, S., Ganguly, S. & Dalal, A. 2013 Buoyancy driven flow and heat transfer of nanofluids past a square cylinder in vertically upward flow. Intl J. Heat Mass Transfer 59, 433–450.CrossRefGoogle Scholar
Sen, S., Mittal, S. & Biswas, G. 2011 Flow past a square cylinder at low Reynolds numbers. Intl J. Numer. Meth. Fluids 67 (9), 1160–1174.CrossRefGoogle Scholar
Sharma, A. & Eswaran, V. 2004 Effect of aiding and opposing buoyancy on the heat and fluid flow across a square cylinder at $Re = 100$. Numer. Heat Transfer 45 (6), 601–624.CrossRefGoogle Scholar
Sharma, A. & Eswaran, V. 2005 Effect of channel-confinement and aiding/opposing buoyancy on the two-dimensional laminar flow and heat transfer across a square cylinder. Intl J. Heat Mass Transfer 48 (25–26), 5310–5322.CrossRefGoogle Scholar
Sohankar, A., Norbergb, C. & Davidson, L. 1997 Numerical simulation of unsteady low-Reynolds number flow around rectangular cylinders at incidence. J. Wind Engng Ind. Aerodyn. 69, 189–201.CrossRefGoogle Scholar
Taddei, S., Manes, C. & Ganapathisubramani, B. 2016 Characterisation of drag and wake properties of canopy patches immersed in turbulent boundary layers. J. Fluid Mech. 798, 27–49.CrossRefGoogle Scholar
Takami, H. & Keller, H.B. 1969 Steady two-dimensional viscous flow of an incompressible fluid past a circular cylinder. Phys. Fluids 12 (12), II–51.CrossRefGoogle Scholar
Tang, T., Yu, P., Shan, X., Chen, H. & Su, J. 2019 Investigation of drag properties for flow through and around square arrays of cylinders at low Reynolds numbers. Chem. Engng Sci. 199, 285–301.CrossRefGoogle Scholar
Tang, T., Yu, P., Shan, X., Li, J. & Yu, S. 2020 On the transition behavior of laminar flow through and around a multi-cylinder array. Phys. Fluids 32 (1), 013601.Google Scholar
Travkin, V.S. & Catton, I. 2001 Transport phenomena in heterogeneous media based on volume averaging theory. In Advances in Heat Transfer (ed. H.G. Garg & C.A. Hales), vol. 34, pp. 1–144. Elsevier.CrossRefGoogle Scholar
Tritton, D.J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6 (4), 547–567.CrossRefGoogle Scholar
Vijaybabu, T.R., Anirudh, K. & Dhinakaran, S. 2017 Mixed convective heat transfer from a permeable square cylinder: a lattice Boltzmann analysis. Intl J. Heat Mass Transfer 115, 854–870.CrossRefGoogle Scholar
Vijaybabu, T.R., Anirudh, K. & Dhinakaran, S. 2018 Lattice Boltzmann simulations of flow and heat transfer from a permeable triangular cylinder under the influence of aiding buoyancy. Intl J. Heat Mass Transfer 117, 799–817.CrossRefGoogle Scholar
Whitaker, S. 1967 Diffusion and dispersion in porous media. AIChE J. 13 (3), 420–427.CrossRefGoogle Scholar
Yu, S., Yu, P. & Tang, T. 2018 Effect of thermal buoyancy on flow and heat transfer around a permeable circular cylinder with internal heat generation. Intl J. Heat Mass Transfer 126, 1143–1163.CrossRefGoogle Scholar
Zargartalebi, M. & Azaiez, J. 2019 Flow dynamics and heat transfer in partially porous microchannel heat sinks. J. Fluid Mech. 875, 1035–1057.CrossRefGoogle Scholar
Zdravkovich, M.M. 1997 Flow Around Circular Cylinders. Fundamentals, vol. 1. Oxford University Press.Google Scholar
Zong, L. & Nepf, H. 2012 Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 691, 368–391.CrossRefGoogle Scholar