Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zaripov, Dinar
Ivashchenko, Vladislav
Mullyadzhanov, Rustam
Li, Renfu
Markovich, Dmitriy
and
Kähler, Christian J.
2021.
Reverse flow phenomenon in duct corners at a low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 8,
Chen, Tao
Liu, Tianshu
and
Wang, Lian-Ping
2021.
Features of surface physical quantities and temporal-spatial evolution of wall-normal enstrophy flux in wall-bounded flows.
Physics of Fluids,
Vol. 33,
Issue. 12,
Arosemena, Arturo A.
Andersson, Ronnie
Andersson, Helge I.
and
Solsvik, Jannike
2021.
Effects of shear-thinning rheology on near-wall turbulent structures.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Positive and negative pairs of fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 8,
Cheng, Cheng
and
Fu, Lin
2022.
Consistency between the attached-eddy model and the inner–outer interaction model: a study of streamwise wall-shear stress fluctuations in a turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Arosemena, A. A.
Ali, H.
and
Solsvik, J.
2022.
Characterization of vortical structures in a stirred tank.
Physics of Fluids,
Vol. 34,
Issue. 2,
Boxho, M.
Rasquin, M.
Toulorge, T.
Dergham, G.
Winckelmans, G.
and
Hillewaert, K.
2022.
Analysis of Space-Time Correlations to Support the Development of Wall-Modeled LES.
Flow, Turbulence and Combustion,
Vol. 109,
Issue. 4,
p.
1081.
Cheng, Cheng
Shyy, Wei
and
Fu, Lin
2022.
Streamwise inclination angle of wall-attached eddies in turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Yuan, Xianxu
Tong, Fulin
Li, Weipeng
Chen, Jianqiang
and
Dong, Siwei
2022.
Wall-attached temperature structures in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 11,
Bae, H. Jane
and
Koumoutsakos, Petros
2022.
Scientific multi-agent reinforcement learning for wall-models of turbulent flows.
Nature Communications,
Vol. 13,
Issue. 1,
Chiarini, Alessandro
Mauriello, Mariadebora
Gatti, Davide
and
Quadrio, Maurizio
2022.
Ascending–descending and direct–inverse cascades of Reynolds stresses in turbulent Couette flow.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Dong, Siwei
Tong, Fulin
Yu, Ming
Chen, Jianqiang
Yuan, Xianxu
and
Wang, Qian
2022.
Effects of wall temperature on two-point statistics of the fluctuating wall shear stress and heat flux in supersonic turbulent boundary layers.
Physics of Fluids,
Vol. 34,
Issue. 6,
Chen, Tao
and
Liu, Tianshu
2023.
Lamb dilatation and its hydrodynamic viscous flux in near-wall incompressible flows.
Physica D: Nonlinear Phenomena,
Vol. 448,
Issue. ,
p.
133730.
Cheng, Cheng
Shyy, Wei
and
Fu, Lin
2023.
Momentum and heat flux events in compressible turbulent channel flows.
Physical Review Fluids,
Vol. 8,
Issue. 9,
Hu, Ruifeng
Dong, Siwei
and
Vinuesa, Ricardo
2023.
General attached eddies: Scaling laws and cascade self-similarity.
Physical Review Fluids,
Vol. 8,
Issue. 4,
Arosemena, Arturo A.
and
Solsvik, Jannike
2023.
Proper orthogonal decomposition modal analysis in a baffled stirred tank: a base tool for the study of structures.
Flow,
Vol. 3,
Issue. ,
Cheng, Cheng
and
Fu, Lin
2023.
A scale-based study of the Reynolds number scaling for the near-wall streamwise turbulence intensity in wall turbulence.
International Journal of Heat and Fluid Flow,
Vol. 101,
Issue. ,
p.
109136.
Yin, Yanxin
Wu, Yongjun
Wang, Run
Ren, Chong
Qu, Qiang
Zhang, Qingqing
and
Liu, Jin
2023.
Positive and negative wall-pressure fluctuations beneath a supersonic turbulent boundary layer.
Acta Mechanica Sinica,
Vol. 39,
Issue. 1,
Cheng, Cheng
and
Fu, Lin
2023.
Linear-model-based study of the coupling between velocity and temperature fields in compressible turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Zhao, Yunchao
Fan, Yitong
and
Li, Weipeng
2024.
Reynolds number effects on a velocity–vorticity correlation-based skin-friction drag decomposition in incompressible turbulent channel flows.
Journal of Fluid Mechanics,
Vol. 979,
Issue. ,
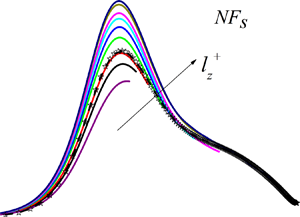
 $\tau _x'$) in turbulent channel flows at different Reynolds numbers. The wall-shear stress structures are identified using a two-dimensional clustering methodology, and two indispensable factors, scale and sign, are considered for the analysis. The structures are classified into positive and negative families according to the sign of
$\tau _x'$) in turbulent channel flows at different Reynolds numbers. The wall-shear stress structures are identified using a two-dimensional clustering methodology, and two indispensable factors, scale and sign, are considered for the analysis. The structures are classified into positive and negative families according to the sign of  $\tau _x'$. The statistical properties of the structures, including geometrical characteristics, spatial distribution, population density, fluctuating intensity, and correlations with outer motions are comprehensively investigated. Particular attention is paid to the asymmetries between positive and negative structures and their connection with wall-attached energy-containing eddies. In virtue of our results, only the large-scale structures of negative
$\tau _x'$. The statistical properties of the structures, including geometrical characteristics, spatial distribution, population density, fluctuating intensity, and correlations with outer motions are comprehensively investigated. Particular attention is paid to the asymmetries between positive and negative structures and their connection with wall-attached energy-containing eddies. In virtue of our results, only the large-scale structures of negative  $\tau _x'$ contain the footprints of the inactive part of wall-attached eddies populating the logarithmic region.
$\tau _x'$ contain the footprints of the inactive part of wall-attached eddies populating the logarithmic region.

