Article contents
On the 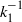 ${ k}_{1}^{- 1} $ scaling in sink-flow turbulent boundary layers
${ k}_{1}^{- 1} $ scaling in sink-flow turbulent boundary layers
Published online by Cambridge University Press: 25 November 2013
Abstract
Scaling of the streamwise velocity spectrum 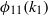 ${\phi }_{11} ({k}_{1} )$ in the so-called sink-flow turbulent boundary layer is investigated in this work. The present experiments show strong evidence for the
${\phi }_{11} ({k}_{1} )$ in the so-called sink-flow turbulent boundary layer is investigated in this work. The present experiments show strong evidence for the 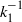 ${ k}_{1}^{- 1} $ scaling i.e.
${ k}_{1}^{- 1} $ scaling i.e. 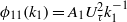 ${\phi }_{11} ({k}_{1} )= {A}_{1} { U}_{\tau }^{2} { k}_{1}^{- 1} $ , where
${\phi }_{11} ({k}_{1} )= {A}_{1} { U}_{\tau }^{2} { k}_{1}^{- 1} $ , where 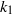 ${k}_{1} $ is the streamwise wavenumber and
${k}_{1} $ is the streamwise wavenumber and 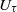 ${U}_{\tau } $ is the friction velocity. Interestingly, this
${U}_{\tau } $ is the friction velocity. Interestingly, this 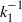 ${ k}_{1}^{- 1} $ scaling is observed much farther from the wall and at much lower flow Reynolds number (both differing by almost an order of magnitude) than what the expectations from experiments on a zero-pressure-gradient turbulent boundary layer flow would suggest. Furthermore, the coefficient
${ k}_{1}^{- 1} $ scaling is observed much farther from the wall and at much lower flow Reynolds number (both differing by almost an order of magnitude) than what the expectations from experiments on a zero-pressure-gradient turbulent boundary layer flow would suggest. Furthermore, the coefficient 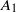 ${A}_{1} $ in the present sink-flow data is seen to be non-universal, i.e.
${A}_{1} $ in the present sink-flow data is seen to be non-universal, i.e. 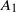 ${A}_{1} $ varies with height from the wall; the scaling exponent −1 remains universal. Logarithmic variation of the so-called longitudinal structure function, which is the physical-space counterpart of spectral
${A}_{1} $ varies with height from the wall; the scaling exponent −1 remains universal. Logarithmic variation of the so-called longitudinal structure function, which is the physical-space counterpart of spectral 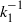 ${ k}_{1}^{- 1} $ scaling, is also seen to be non-universal, consistent with the non-universality of
${ k}_{1}^{- 1} $ scaling, is also seen to be non-universal, consistent with the non-universality of 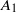 ${A}_{1} $ . These observations are to be contrasted with the universal value of
${A}_{1} $ . These observations are to be contrasted with the universal value of 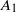 ${A}_{1} $ (along with the universal scaling exponent of −1) reported in the literature on zero-pressure-gradient turbulent boundary layers. Theoretical arguments based on dimensional analysis indicate that the presence of a streamwise pressure gradient in sink-flow turbulent boundary layers makes the coefficient
${A}_{1} $ (along with the universal scaling exponent of −1) reported in the literature on zero-pressure-gradient turbulent boundary layers. Theoretical arguments based on dimensional analysis indicate that the presence of a streamwise pressure gradient in sink-flow turbulent boundary layers makes the coefficient 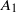 ${A}_{1} $ non-universal while leaving the scaling exponent −1 unaffected. This effect of the pressure gradient on the streamwise spectra, as discussed in the present study (experiments as well as theory), is consistent with other recent studies in the literature that are focused on the structural aspects of turbulent boundary layer flows in pressure gradients (Harun et al., J. Fluid Mech., vol. 715, 2013, pp. 477–498); the present paper establishes the link between these two. The variability of
${A}_{1} $ non-universal while leaving the scaling exponent −1 unaffected. This effect of the pressure gradient on the streamwise spectra, as discussed in the present study (experiments as well as theory), is consistent with other recent studies in the literature that are focused on the structural aspects of turbulent boundary layer flows in pressure gradients (Harun et al., J. Fluid Mech., vol. 715, 2013, pp. 477–498); the present paper establishes the link between these two. The variability of 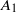 ${A}_{1} $ accommodated in the present framework serves to clarify the ideas of universality of the
${A}_{1} $ accommodated in the present framework serves to clarify the ideas of universality of the 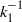 ${ k}_{1}^{- 1} $ scaling.
${ k}_{1}^{- 1} $ scaling.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 7
- Cited by

