Article contents
On the interaction of a compliant wall with a turbulent boundary layer
Published online by Cambridge University Press: 23 July 2020
Abstract
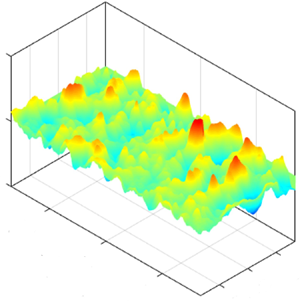
This study examines the interactions of a compliant wall with a turbulent boundary layer as the deformation scale increases from submicron to several wall units (δν). The friction velocity Reynolds number ranges between 1435 and 5179, and  $E/\rho U_0^2$, where E is the Young modulus, varies from 59 to 2.4,
$E/\rho U_0^2$, where E is the Young modulus, varies from 59 to 2.4,  $\rho $ is fluid density and
$\rho $ is fluid density and  $ U_0$ is free-stream velocity. Time-resolved Mach–Zehnder interferometry is used for measuring the spatial distribution of the surface deformation, and two-dimensional (2-D) particle image velocimetry for measuring the velocity in the inner part of the boundary layer. Reynolds stresses and two-point correlations are measured in the log layer. The deformation amplitude increases from 0.02δν at
$ U_0$ is free-stream velocity. Time-resolved Mach–Zehnder interferometry is used for measuring the spatial distribution of the surface deformation, and two-dimensional (2-D) particle image velocimetry for measuring the velocity in the inner part of the boundary layer. Reynolds stresses and two-point correlations are measured in the log layer. The deformation amplitude increases from 0.02δν at  $E/\rho U_0^2 = 59$ to 3.6δν at
$E/\rho U_0^2 = 59$ to 3.6δν at  $E/\rho U_0^2 = 2.4$. Wavenumber–frequency and 2-D spatial spectra show that the deformations consist of two modes: The first is an advected mode that travels downstream at 66 % of U0, has a lattice-like structure and a preferential spanwise alignment. The amplitude and frequency of this mode agree with the Chase (J. Acoust. Soc. Am., vol. 89, no. 6, 1991, pp. 2589–2596) and Benschop et al. (J. Fluid Mech., vol. 859, 2019, pp. 613–658) model predictions. The second mode is a streamwise-aligned wave that travels at the material shear speed (Ct = 7.85 m s−1) in the spanwise direction and has a wavelength of three times the compliant layer thickness. With decreasing
$E/\rho U_0^2 = 2.4$. Wavenumber–frequency and 2-D spatial spectra show that the deformations consist of two modes: The first is an advected mode that travels downstream at 66 % of U0, has a lattice-like structure and a preferential spanwise alignment. The amplitude and frequency of this mode agree with the Chase (J. Acoust. Soc. Am., vol. 89, no. 6, 1991, pp. 2589–2596) and Benschop et al. (J. Fluid Mech., vol. 859, 2019, pp. 613–658) model predictions. The second mode is a streamwise-aligned wave that travels at the material shear speed (Ct = 7.85 m s−1) in the spanwise direction and has a wavelength of three times the compliant layer thickness. With decreasing  $E/\rho U_0^2$, the velocity profiles in the boundary layer increasingly deviate from those of a rigid smooth wall. Yet, these deviations begin when the deformation is 0.02δν. The most prominent features are a sharp decrease in velocity at y < 10δν and an increase in the near-wall turbulence, both consistent, for matching
$E/\rho U_0^2$, the velocity profiles in the boundary layer increasingly deviate from those of a rigid smooth wall. Yet, these deviations begin when the deformation is 0.02δν. The most prominent features are a sharp decrease in velocity at y < 10δν and an increase in the near-wall turbulence, both consistent, for matching  $E/\rho U_0^2$, with the direct numerical simulation results of Rosti and Brandt (J. Fluid Mech., vol. 830, 2017, pp. 708–735).
$E/\rho U_0^2$, with the direct numerical simulation results of Rosti and Brandt (J. Fluid Mech., vol. 830, 2017, pp. 708–735).
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
Wang et al. supplementary movie 1
- 16
- Cited by

