Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Valero, Daniel
and
Bung, Daniel B.
2018.
Reformulating self-aeration in hydraulic structures: Turbulent growth of free surface perturbations leading to air entrainment.
International Journal of Multiphase Flow,
Vol. 100,
Issue. ,
p.
127.
Termini, Donatella
and
Moramarco, Tommaso
2018.
Dip Phenomenon in High-Curved Turbulent Flows and Application of Entropy Theory.
Water,
Vol. 10,
Issue. 3,
p.
306.
Herlina, H.
and
Wissink, J. G.
2019.
Simulation of air–water interfacial mass transfer driven by high-intensity isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
419.
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
and
Champagne, J.-Y.
2020.
Oscillating grid generating turbulence near gas-liquid interfaces in shear-thinning dilute polymer solutions.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Wissink, J. G.
and
Herlina, H.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
17.
Valero, Daniel
Chanson, Hubert
and
Bung, Daniel B.
2020.
Robust estimators for free surface turbulence characterization: a stepped spillway application.
Flow Measurement and Instrumentation,
Vol. 76,
Issue. ,
p.
101809.
Bourgoin, Adrien
El Kadi Abderrezzak, Kamal
Benhamadouche, Sofiane
and
Ata, Riadh
2021.
An adoption of the Spalart–Allmaras turbulence model for two- and three-dimensional free surface environmental flows.
Journal of Hydraulic Research,
Vol. 59,
Issue. 2,
p.
314.
Guseva, S.
Aurela, M.
Cortés, A.
Kivi, R.
Lotsari, E.
MacIntyre, S.
Mammarella, I.
Ojala, A.
Stepanenko, V.
Uotila, P.
Vähä, A.
Vesala, T.
Wallin, M. B.
and
Lorke, A.
2021.
Variable Physical Drivers of Near‐Surface Turbulence in a Regulated River.
Water Resources Research,
Vol. 57,
Issue. 11,
Issaev, Vassili
Williamson, N.
Armfield, S.W.
and
Norris, S.E.
2022.
Parameterization of mixing in stratified open channel flow.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Lacassagne, Tom
EL Hajem, Mahmoud
Champagne, Jean-Yves
and
Simoëns, Serge
2022.
Turbulent mass transfer near gas-liquid interfaces in water and shear-thinning dilute polymer solution.
International Journal of Heat and Mass Transfer,
Vol. 194,
Issue. ,
p.
122975.
Wu, Huijie
and
Wang, Binbin
2023.
Spectral turbulence kinetic energy budget and scale-based velocity decomposition for turbulence in bubble plumes.
Physics of Fluids,
Vol. 35,
Issue. 6,
Issaev, Vassili
Williamson, N.
and
Armfield, S.W.
2023.
Intermittency and critical mixing in internally heated stratified channel flow.
Journal of Fluid Mechanics,
Vol. 963,
Issue. ,
Sanness Salmon, Henri R.
Baker, Lucia J.
Kozarek, Jessica L.
and
Coletti, Filippo
2023.
Effect of Shape and Size on the Transport of Floating Particles on the Free Surface in a Natural Stream.
Water Resources Research,
Vol. 59,
Issue. 10,
Ruth, Daniel J.
and
Coletti, Filippo
2024.
Structure and energy transfer in homogeneous turbulence below a free surface.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
Aarnes, Jørgen R.
Babiker, Omer M.
Xuan, Anqing
Shen, Lian
and
Ellingsen, Simen Å.
2025.
Vortex structures under dimples and scars in turbulent free-surface flows.
Journal of Fluid Mechanics,
Vol. 1007,
Issue. ,
Jamin, Timothée
Berhanu, Michael
and
Falcon, Eric
2025.
Experimental study of three-dimensional turbulence under a free surface.
Physical Review Fluids,
Vol. 10,
Issue. 3,
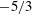 $-5/3$ spectra for the horizontal velocities.
$-5/3$ spectra for the horizontal velocities.

