Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Savva, Nikos
Rednikov, Alexey
and
Colinet, Pierre
2017.
Asymptotic analysis of the evaporation dynamics of partially wetting droplets.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
574.
Hammoud, Naima H.
Trinh, Philippe H.
Howell, Peter D.
and
Stone, Howard A.
2017.
Influence of van der Waals forces on a bubble moving in a tube.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Jhangeer, Adil
2018.
Group Classification, Reductions and Exact Solutions of a Class of Higher Order Nonlinear Degenerate Parabolic Equation.
International Journal of Applied and Computational Mathematics,
Vol. 4,
Issue. 1,
Arash, Azimi
He, Ping
Rohrs, Chae
and
Yao, Chun-Wei
2018.
Developing a novel continuum model of static and dynamic contact angles in a case study of a water droplet on micro-patterned hybrid substrates.
MRS Communications,
Vol. 8,
Issue. 4,
p.
1445.
Wang, Dong
Wang, Xiao-Ping
and
Xu, Xianmin
2019.
An improved threshold dynamics method for wetting dynamics.
Journal of Computational Physics,
Vol. 392,
Issue. ,
p.
291.
Xu, Xianmin
Zhao, Yinyu
and
Wang, Xiaoping
2019.
Analysis for Contact Angle Hysteresis on Rough Surfaces by a Phase-Field Model with a Relaxed Boundary Condition.
SIAM Journal on Applied Mathematics,
Vol. 79,
Issue. 6,
p.
2551.
Zhang, Zhen
and
Ren, Weiqing
2019.
Distinguished Limits of the Navier Slip Model for Moving Contact Lines in Stokes Flow.
SIAM Journal on Applied Mathematics,
Vol. 79,
Issue. 5,
p.
1654.
Wang, Shuai
Ryu, Jaeha
He, Guo-Qiang
Qin, Fei
and
Sung, Hyung Jin
2020.
A self-propelled flexible plate with a Navier slip surface.
Physics of Fluids,
Vol. 32,
Issue. 2,
Hooshanginejad, Alireza
Dutcher, Cari
Shelley, Michael J.
and
Lee, Sungyon
2020.
Droplet breakup in a stagnation-point flow.
Journal of Fluid Mechanics,
Vol. 901,
Issue. ,
Zhang, Zhen
Yao, Jin
and
Ren, Weiqing
2020.
Static interface profiles for contact lines on an elastic membrane with the Willmore energy.
Physical Review E,
Vol. 102,
Issue. 6,
Zhao, Quan
and
Ren, Weiqing
2020.
An energy-stable finite element method for the simulation of moving contact lines in two-phase flows.
Journal of Computational Physics,
Vol. 417,
Issue. ,
p.
109582.
Yin, Hongna
Huang, Xingyuan
Liu, Tongke
and
Song, Minjie
2021.
Effects of gas-assisted extrusion on slip in the cable coating process.
Journal of Polymer Engineering,
Vol. 41,
Issue. 4,
p.
329.
Zhao, Quan
Ren, Weiqing
and
Zhang, Zhen
2021.
A thermodynamically consistent model and its conservative numerical approximation for moving contact lines with soluble surfactants.
Computer Methods in Applied Mechanics and Engineering,
Vol. 385,
Issue. ,
p.
114033.
Yonemoto, Yukihiro
Tashiro, Kanta
Shimizu, Kazuki
and
Kunugi, Tomoaki
2022.
Predicting the splash of a droplet impinging on solid substrates.
Scientific Reports,
Vol. 12,
Issue. 1,
Zhang, Zhen
and
Xu, Xianmin
2022.
Effective boundary conditions for dynamic contact angle hysteresis on chemically inhomogeneous surfaces.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Deng, Xiaozhen
Xiao, Bing
Ren, Zhong
Zhu, Zhifang
and
Liu, Biao
2022.
Effects of gas-assisted technology on polymer micro coextrusion.
Journal of Polymer Engineering,
Vol. 42,
Issue. 10,
p.
986.
Mantripragada, Vishnu Teja
and
Poddar, Antarip
2022.
Rheology dictated spreading regimes of a non-isothermal sessile drop.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
KAKAMU, Souta
ITO, Takahiro
and
TSUJI, Yoshiyuki
2023.
Molecular dynamics analysis for the effect of the wettability and the slip on the solid wall surface on bubble growth.
Transactions of the JSME (in Japanese),
Vol. 89,
Issue. 927,
p.
22-00320.
Liu, Haishuo
Zhang, Zipeng
Wu, Chenyu
Su, Kang
and
Kan, Xiaonan
2023.
Biomimetic Superhydrophobic Materials through 3D Printing: Progress and Challenges.
Micromachines,
Vol. 14,
Issue. 6,
p.
1216.
Feng, Zhe
2025.
Two-dimensional electroconvective flows between Navier-slip boundaries.
Physical Review Fluids,
Vol. 10,
Issue. 8,
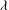 ${\it\lambda}$ , serves to alleviate. In this paper, we discuss what occurs as the slip parameter,
${\it\lambda}$ , serves to alleviate. In this paper, we discuss what occurs as the slip parameter, 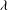 ${\it\lambda}$ , tends to zero. In particular, we explain how the zero-slip limit should be discussed in consideration of two distinguished limits: one where time is held constant,
${\it\lambda}$ , tends to zero. In particular, we explain how the zero-slip limit should be discussed in consideration of two distinguished limits: one where time is held constant, 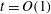 $t=O(1)$ , and one where time tends to infinity at the rate
$t=O(1)$ , and one where time tends to infinity at the rate 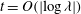 $t=O(|\!\log {\it\lambda}|)$ . The crucial result is that in the case where time is held constant, the
$t=O(|\!\log {\it\lambda}|)$ . The crucial result is that in the case where time is held constant, the  ${\it\lambda}\rightarrow 0$ limit converges to the slip-free equation, and contact line slippage occurs as a regular perturbative effect. However, if
${\it\lambda}\rightarrow 0$ limit converges to the slip-free equation, and contact line slippage occurs as a regular perturbative effect. However, if 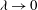 ${\it\lambda}\rightarrow 0$ and
${\it\lambda}\rightarrow 0$ and 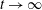 $t\rightarrow \infty$ , then contact line slippage is a leading-order singular effect.
$t\rightarrow \infty$ , then contact line slippage is a leading-order singular effect.

