Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lamb, Kevin G.
and
Nguyen, Van T.
2009.
Calculating Energy Flux in Internal Solitary Waves with an Application to Reflectance.
Journal of Physical Oceanography,
Vol. 39,
Issue. 3,
p.
559.
Warn-Varnas, A.
Hawkins, J.
Lamb, K.G.
Piacsek, S.
Chin-Bing, S.
King, D.
and
Burgos, G.
2010.
Solitary wave generation dynamics at Luzon Strait.
Ocean Modelling,
Vol. 31,
Issue. 1-2,
p.
9.
Klymak, Jody M.
and
Legg, Sonya M.
2010.
A simple mixing scheme for models that resolve breaking internal waves.
Ocean Modelling,
Vol. 33,
Issue. 3-4,
p.
224.
Kang, Dujuan
and
Fringer, Oliver
2010.
On the Calculation of Available Potential Energy in Internal Wave Fields.
Journal of Physical Oceanography,
Vol. 40,
Issue. 11,
p.
2539.
Sanford, Thomas B.
Price, James F.
and
Girton, James B.
2011.
Upper-Ocean Response to Hurricane Frances (2004) Observed by Profiling EM-APEX Floats*.
Journal of Physical Oceanography,
Vol. 41,
Issue. 6,
p.
1041.
Lamb, Kevin G.
and
Farmer, David
2011.
Instabilities in an Internal Solitary-like Wave on the Oregon Shelf.
Journal of Physical Oceanography,
Vol. 41,
Issue. 1,
p.
67.
KING, STUART E.
CARR, MAGDA
and
DRITSCHEL, DAVID G.
2011.
The steady-state form of large-amplitude internal solitary waves.
Journal of Fluid Mechanics,
Vol. 666,
Issue. ,
p.
477.
Bourgault, Daniel
Janes, David C.
and
Galbraith, Peter S.
2011.
Observations of a Large-Amplitude Internal Wave Train and Its Reflection off a Steep Slope.
Journal of Physical Oceanography,
Vol. 41,
Issue. 3,
p.
586.
Camassa, Roberto
and
Viotti, Claudio
2012.
On the response of large-amplitude internal waves to upstream disturbances.
Journal of Fluid Mechanics,
Vol. 702,
Issue. ,
p.
59.
Tailleux, Rémi
2013.
Available potential energy density for a multicomponent Boussinesq fluid with arbitrary nonlinear equation of state.
Journal of Fluid Mechanics,
Vol. 735,
Issue. ,
p.
499.
Tailleux, Rémi
2013.
Available Potential Energy and Exergy in Stratified Fluids.
Annual Review of Fluid Mechanics,
Vol. 45,
Issue. 1,
p.
35.
Xie, Jieshuo
Chen, Zhiwu
Xu, Jiexin
and
Cai, Shuqun
2014.
Effect of vertical stratification on characteristics and energy of nonlinear internal solitary waves from a numerical model.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 19,
Issue. 10,
p.
3539.
Lamb, Kevin G.
and
Xiao, Wenting
2014.
Internal solitary waves shoaling onto a shelf: Comparisons of weakly-nonlinear and fully nonlinear models for hyperbolic-tangent stratifications.
Ocean Modelling,
Vol. 78,
Issue. ,
p.
17.
Zhang, Weifeng G.
and
Gawarkiewicz, Glen G.
2015.
Length Scale of the Finite-Amplitude Meanders of Shelfbreak Fronts.
Journal of Physical Oceanography,
Vol. 45,
Issue. 10,
p.
2598.
Xie, Jieshuo
He, Yinghui
Chen, Zhiwu
Xu, Jiexin
and
Cai, Shuqun
2015.
Simulations of Internal Solitary Wave Interactions with Mesoscale Eddies in the Northeastern South China Sea.
Journal of Physical Oceanography,
Vol. 45,
Issue. 12,
p.
2959.
Xie, Jieshuo
Pan, Jiayi
and
Jay, David A.
2015.
Multimodal Internal Waves Generated over a Subcritical Ridge: Impact of the Upper-Ocean Stratification.
Journal of Physical Oceanography,
Vol. 45,
Issue. 3,
p.
904.
Lü, Haibin
Xie, Jieshuo
Yao, Yuan
Xu, Jiexin
Chen, Zhiwu
He, Yinghui
and
Cai, Shuqun
2016.
Effect of background parabolic current on characteristics and energetics of internal solitary waves by numerical simulation.
Acta Oceanologica Sinica,
Vol. 35,
Issue. 1,
p.
1.
Rivera‐Rosario, Gustavo A.
Diamessis, Peter J.
and
Jenkins, James T.
2017.
Bed failure induced by internal solitary waves.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 7,
p.
5468.
Cheng, Ming-Hung
Hsieh, Chih-Min
Hsu, John R.-C.
and
Hwang, Robert R.
2017.
Effect of porosity on an internal solitary wave propagating over a porous trapezoidal obstacle.
Ocean Engineering,
Vol. 130,
Issue. ,
p.
126.
Bai, Xiaolin
Li, Xiaofeng
Lamb, Kevin G.
and
Hu, Jianyu
2017.
Internal Solitary Wave Reflection Near Dongsha Atoll, the South China Sea.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 10,
p.
7978.
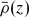 can be used as the reference density if Ea is used to find the APE. This is not the case when Ew is used, hence use of the available potential energy density formulation is simpler in this situation.
can be used as the reference density if Ea is used to find the APE. This is not the case when Ew is used, hence use of the available potential energy density formulation is simpler in this situation.
