Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gonzalo, A.
Arranz, G.
Moriche, M.
García-Villalba, M.
and
Flores, O.
2018.
From flapping to heaving: A numerical study of wings in forward flight.
Journal of Fluids and Structures,
Vol. 83,
Issue. ,
p.
293.
Lin, Yung-Sheng
Tzeng, Yau-Ting
Hsieh, Cheng-Ta
Chang, Chien C.
and
Chu, Chin-Chou
2018.
A mechanism of thrust enhancement on a heaving plate due to flexibility at moderately low Reynolds numbers.
Journal of Fluids and Structures,
Vol. 76,
Issue. ,
p.
573.
Arranz, G
Moriche, M
Uhlmann, M
Flores, O
and
García-Villalba, M
2018.
Kinematics and dynamics of the auto-rotation of a model winged seed.
Bioinspiration & Biomimetics,
Vol. 13,
Issue. 3,
p.
036011.
Arranz, Gonzalo
Gonzalo, Alejandro
Uhlmann, Markus
Flores, Oscar
and
García-Villalba, Manuel
2018.
A Numerical Study of the Flow Around a Model Winged Seed in Auto-Rotation.
Flow, Turbulence and Combustion,
Vol. 101,
Issue. 2,
p.
477.
Ayancik, Fatma
Zhong, Qiang
Quinn, Daniel B.
Brandes, Aaron
Bart-Smith, Hilary
and
Moored, Keith W.
2019.
Scaling laws for the propulsive performance of three-dimensional pitching propulsors.
Journal of Fluid Mechanics,
Vol. 871,
Issue. ,
p.
1117.
Lin, Xingjian
Wu, Jie
and
Zhang, Tongwei
2019.
Performance investigation of a self-propelled foil with combined oscillating motion in stationary fluid.
Ocean Engineering,
Vol. 175,
Issue. ,
p.
33.
Jardin, T.
and
Doué, N.
2019.
Influence of pitch rate on freely translating perching airfoils.
Journal of Fluid Mechanics,
Vol. 873,
Issue. ,
p.
49.
Siala, Firas F.
and
Liburdy, James A.
2019.
Leading-edge vortex dynamics and impulse-based lift force analysis of oscillating airfoils.
Experiments in Fluids,
Vol. 60,
Issue. 10,
Shanmugam, A. R.
and
Sohn, C. H.
2019.
Numerical investigation on thrust production and unsteady mechanisms of three-dimensional oscillating wing.
Journal of Mechanical Science and Technology,
Vol. 33,
Issue. 12,
p.
5889.
Martín-Alcántara, A.
and
Fernandez-Feria, R.
2019.
Assessment of two vortex formulations for computing forces of a flapping foil at high Reynolds numbers.
Physical Review Fluids,
Vol. 4,
Issue. 2,
Moriche, Manuel
Gonzalo, Alejandro
Flores, Oscar
and
Garcia-Villalba, Manuel
2019.
Fast transverse maneuvers at low Reynolds numbers.
Kurtulus, Dilek Funda
2019.
Unsteady aerodynamics of a pitching NACA 0012 airfoil at low Reynolds number.
International Journal of Micro Air Vehicles,
Vol. 11,
Issue. ,
Arranz, G.
Flores, O.
and
García-Villalba, M.
2020.
Three-dimensional effects on the aerodynamic performance of flapping wings in tandem configuration.
Journal of Fluids and Structures,
Vol. 94,
Issue. ,
p.
102893.
Martínez-Muriel, C.
and
Flores, O.
2020.
Analysis of vortical gust impact on airfoils at low Reynolds number.
Journal of Fluids and Structures,
Vol. 99,
Issue. ,
p.
103138.
Zheng, Hongyu
Xie, Fangfang
Ji, Tingwei
and
Zheng, Yao
2020.
Kinematic parameter optimization of a flapping ellipsoid wing based on the data-informed self-adaptive quasi-steady model.
Physics of Fluids,
Vol. 32,
Issue. 4,
Moriche, Manuel
Flores, Oscar
Sedky, Girguis
Jones, Anya R.
and
Garcia-Villalba, Manuel
2020.
Comparison between experiments and simulations of fast tranverse plunge maneuvers.
Arranz, G.
Flores, O.
and
García-Villalba, M.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
297.
Zhang, Mengjie
Liu, Taotao
Huang, Biao
Wu, Qin
and
Wang, Guoyu
2020.
Hydrodynamic characteristics and flow structures of pitching hydrofoil with special emphasis on the added force effect.
Renewable Energy,
Vol. 157,
Issue. ,
p.
560.
Flores, O.
Rossini, L.
Gonzalo, A.
Vigneault, D.
Bermejo, J.
Kahn, A. M.
McVeigh, E.
García-Villalba, M.
and
C. del Álamo, J.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
485.
Moriche, M
Raiola, M
Discetti, S
Ianiro, A
Flores, O
and
García-Villalba, M
2020.
Assessing aerodynamic force estimation with experiments and simulations of flapping-airfoil flows on the verge of three-dimensionality.
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering,
Vol. 234,
Issue. 2,
p.
428.
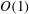 $O(1)$ , varying the mean pitch angle and the phase shift between the pitching and heaving motions. Our results show that the surface vorticity contribution (viscous effect) to the aerodynamic force is negligible compared with the contributions from the body motion (fluid inertia) and the vorticity within the flow (circulation). For the range of parameters considered here, the latter tends to be instantaneously oriented in the direction normal to the chord of the airfoil. Based on the results discussed in this paper, a reduced-order model for the instantaneous aerodynamic force is proposed, taking advantage of the force decomposition and the chord-normal orientation of the contribution from vorticity within the flow to the total aerodynamic force. The predictions of the proposed model are compared with those of a similar model from the literature, showing a noticeable improvement in the prediction of the mean thrust, and a smaller improvement in the prediction of the mean lift and the instantaneous force coefficients.
$O(1)$ , varying the mean pitch angle and the phase shift between the pitching and heaving motions. Our results show that the surface vorticity contribution (viscous effect) to the aerodynamic force is negligible compared with the contributions from the body motion (fluid inertia) and the vorticity within the flow (circulation). For the range of parameters considered here, the latter tends to be instantaneously oriented in the direction normal to the chord of the airfoil. Based on the results discussed in this paper, a reduced-order model for the instantaneous aerodynamic force is proposed, taking advantage of the force decomposition and the chord-normal orientation of the contribution from vorticity within the flow to the total aerodynamic force. The predictions of the proposed model are compared with those of a similar model from the literature, showing a noticeable improvement in the prediction of the mean thrust, and a smaller improvement in the prediction of the mean lift and the instantaneous force coefficients.

