Article contents
On shoaling of solitary waves
Published online by Cambridge University Press: 13 June 2018
Abstract
One of the classic analytical predictions of shoaling-wave amplification is Green’s law – the wave amplitude grows proportional to 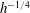 $h^{-1/4}$ , where
$h^{-1/4}$ , where 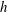 $h$ is the local water depth. Green’s law is valid for linear shallow-water waves unidirectionally propagating in a gradually varying water depth. On the other hand, conservation of mechanical energy shows that the shoaling-wave amplitude of a solitary wave grows like
$h$ is the local water depth. Green’s law is valid for linear shallow-water waves unidirectionally propagating in a gradually varying water depth. On the other hand, conservation of mechanical energy shows that the shoaling-wave amplitude of a solitary wave grows like 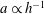 $a\propto h^{-1}$ , if the waveform maintains its solitary-wave identity. Nonetheless, some recent laboratory and field measurements indicate that growth of long waves during shoaling is slower than what is predicted by Green’s law. Obvious missing factors in Green’s law are the nonlinearity and frequency-dispersion effects as well as wave reflection from the beach, whereas the adiabatic shoaling process does not recognize the transformation of the waveform on a beach of finite slope and length. Here we first examine this problem analytically based on the variable-coefficient perturbed Korteweg–de Vries equation. Three analytical solutions for different limits are obtained: (1) Green’s law for the linear and non-dispersive limit, (2) the slower amplitude growth rate for the linear and dispersive limit, as well as (3) nonlinear and non-dispersive limit. Then, in order to characterize the shoaling behaviours for a variety of incident wave and beach conditions, we implement a fifth-order pseudo-spectral numerical model for the full water-wave Euler theory. We found that Green’s law is not the norm but is limited to small incident-wave amplitudes when the wavelength is still small in comparison to the beach length scale. In general, the wave amplification rate during shoaling does not follow a power law. When the incident wave is finite, the shoaling amplification becomes faster than that of Green’s law when the ratio of the wavelength to the beach length is small, but becomes slower when the length ratio increases. We also found that the incident wave starts to amplify prior to its crest arriving at the beach toe due to the wave reflection. Other prominent characteristics and behaviours of solitary-wave shoaling are discussed.
$a\propto h^{-1}$ , if the waveform maintains its solitary-wave identity. Nonetheless, some recent laboratory and field measurements indicate that growth of long waves during shoaling is slower than what is predicted by Green’s law. Obvious missing factors in Green’s law are the nonlinearity and frequency-dispersion effects as well as wave reflection from the beach, whereas the adiabatic shoaling process does not recognize the transformation of the waveform on a beach of finite slope and length. Here we first examine this problem analytically based on the variable-coefficient perturbed Korteweg–de Vries equation. Three analytical solutions for different limits are obtained: (1) Green’s law for the linear and non-dispersive limit, (2) the slower amplitude growth rate for the linear and dispersive limit, as well as (3) nonlinear and non-dispersive limit. Then, in order to characterize the shoaling behaviours for a variety of incident wave and beach conditions, we implement a fifth-order pseudo-spectral numerical model for the full water-wave Euler theory. We found that Green’s law is not the norm but is limited to small incident-wave amplitudes when the wavelength is still small in comparison to the beach length scale. In general, the wave amplification rate during shoaling does not follow a power law. When the incident wave is finite, the shoaling amplification becomes faster than that of Green’s law when the ratio of the wavelength to the beach length is small, but becomes slower when the length ratio increases. We also found that the incident wave starts to amplify prior to its crest arriving at the beach toe due to the wave reflection. Other prominent characteristics and behaviours of solitary-wave shoaling are discussed.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 26
- Cited by


