No CrossRef data available.
Article contents
On linear and nonlinear acoustics in stratified variable-area ducts and atmospheres and Lighthill's proposition
Published online by Cambridge University Press: 11 March 2021
Abstract
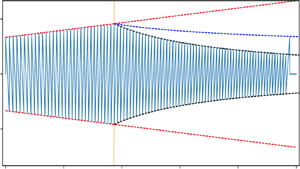
We consider linear and nonlinear waves in a stratified hydrostatic fluid within a channel of variable area, under the restriction of one-dimensional flow. We derive a modified version of Riemann's invariant that is related to the wave luminosity. This quantity obeys a simple dynamical equation in linear theory, from which the rules of wave reflection are easily discerned; and it is adiabatically conserved in the high-frequency limit. Following a suggestion by Lighthill, we apply the linear adiabatic invariant to predict mildly nonlinear waves. This incurs only moderate error. We find that Lighthill's criterion for shock formation is essentially exact for leading shocks, and for shocks within high-frequency waves. We conclude that approximate invariants can be used to accurately predict the self-distortion of low-amplitude acoustic pulses, as well as the dissipation patterns for weak shocks, in complicated environments such as stellar envelopes. We also identify fully nonlinear solutions for a restricted class of problems.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press


