Hostname: page-component-5b777bbd6c-v4w92 Total loading time: 0 Render date: 2025-06-24T12:17:03.211Z Has data issue: false hasContentIssue false
  • English
  • Français

On dewetting and concentration evolution of thin binary fluid films

Published online by Cambridge University Press:  14 November 2024

J.A. Diez Open the ORCID record for J.A. Diez [Opens in a new window] ,
A.G. González Open the ORCID record for A.G. González [Opens in a new window]  and
L. Kondic Open the ORCID record for L. Kondic [Opens in a new window]
J.A. Diez
Affiliation:
Instituto de Física Arroyo Seco, Universidad Nacional del Centro de la Provincia de Buenos Aires, and CIFICEN-CONICET-CICPBA, Pinto 399, 7000, Tandil, Argentina
A.G. González*
Affiliation:
Instituto de Física Arroyo Seco, Universidad Nacional del Centro de la Provincia de Buenos Aires, and CIFICEN-CONICET-CICPBA, Pinto 399, 7000, Tandil, Argentina
L. Kondic
Affiliation:
Department of Mathematical Sciences and Center for Applied Mathematics and Statistics, New Jersey Institute of Technology, Newark, NJ 07102, USA
*
†Email address for correspondence: aggonzal@exa.unicen.edu.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

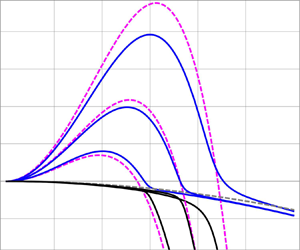
We study the stability and dewetting dynamics of a thin free-surface film composed of two miscible liquids placed on a solid substrate. Our study focuses on the development of a self-consistent model such that the mixture concentration influences both free-surface and wetting energies. By assuming a simple relation between these energies and the bulk and surface concentrations, we analyse their effect on the concentration distribution and dewetting down to the equilibrium film thickness determined by the fluid–solid interaction potential. The model, developed within the gradient dynamics formulation, includes the dependence of the free-surface energy on surface concentration leading to the Marangoni effect, while a composition-dependent Hamaker constant describes the wetting energy resulting from the fluid–solid interaction. We analyse the restrictions that must be fulfilled to ensure an equilibrium state for a flat film of a binary fluid. Then, we proceed by studying its linear stability. First, we consider the Marangoni effect while assuming that wetting energy depends only on the fluid thickness. Then, we include a dependence of wetting energy on concentration and study its effects. We find that the linear stability results compare very well with those of numerical simulations of the full nonlinear problem applied to the particular case of a binary melted metal alloy, even close to breakup times. Therefore, in practice, most of the evolution can be studied by using the linear theory, simplifying the problem considerably.

JFM classification

Interfacial Flows (free surface): Thin films Multiphase and Particle-laden Flows: Multiphase flow Mass Transport: Coupled diffusion and flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 999 , 25 November 2024 , A55
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Archer, A.J., Ionescu, C., Pini, D. & Reatto, L. 2008 Theory for the phase behavior of a colloidal fluid with competing interactions. J. Phys.: Condens. Matter 20, 415106.Google Scholar
Archer, A.J., Pini, D., Evans, R. & Reatto, L. 2007 Model colloidal fluid with competing interactions: bulk and interfacial properties. J. Chem. Phys. 126, 014104.CrossRefGoogle ScholarPubMed
Areshi, M., Tseluiko, D., Thiele, U., Goddard, B.D. & Archer, A.J. 2024 Binding potential and wetting behavior of binary liquid mixtures on surfaces. Phys. Rev. E 109, 024801.CrossRefGoogle ScholarPubMed
Cahn, J.W. 1965 Phase separation by spinodal decomposition in isotropic systems. J. Chem. Phys. 42, 93–99.CrossRefGoogle Scholar
Cahn, J.W. & Hilliard, J.E. 1958 Free energy of a nonuniform system. 1. Interfacial free energy. J. Chem. Phys. 28, 258–267.CrossRefGoogle Scholar
Chao, Y., Ramírez-Soto, O., Bahr, C. & Karpitschka, S. 2022 How liquid–liquid phase separation induces active spreading. Proc. Natl Acad. Sci. 119, 2203510119.CrossRefGoogle ScholarPubMed
Clarke, N. 2005 Toward a model for pattern formation in ultrathin-film binary mixtures. Macromolecules 38, 6775–6778.CrossRefGoogle Scholar
Craster, R.V. & Matar, O.K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131.CrossRefGoogle Scholar
Diamant, H. & Andelman, D. 1996 Kinetics of surfactant adsorption at fluid-fluid interfaces. J. Phys. Chem. 100, 13732–13742.CrossRefGoogle Scholar
Diez, J.A., González, A.G., Garfinkel, D.A., Rack, P.D., McKeown, J.T. & Kondic, L. 2021 Simultaneous decomposition and dewetting of nanoscale alloys: a comparison of experiment and theory. Langmuir 37, 2575–2585.CrossRefGoogle ScholarPubMed
Doi, M. 2011 Onsager's variational principle in soft matter. J. Phys.: Condens. Matter 23, 284118.Google ScholarPubMed
Hughes, R.A., Menumerov, E. & Neretina, S. 2017 When lithography meets self-assembly: a review of recent advances in the directed assembly of complex metal nanostructures on planar and textured surfaces. Nanotechnology 28, 282002.CrossRefGoogle ScholarPubMed
Huth, R., Jachalski, S., Kitavtsev, G. & Peschka, D. 2015 Gradient flow perspective on thin-film bilayer flows. J. Engng Maths 94, 43–61.CrossRefGoogle Scholar
Joseph, D.D., Bai, R., Chen, K.P. & Renardy, Y.Y. 1997 Core-annular flows. Annu. Rev. Fluid Mech. 29, 65–90.CrossRefGoogle Scholar
Joseph, D.D. & Renardy, Y.Y. 1992 a Fundamentals of Two-Fluid Dynamics. Volume 1: Mathematical Theory and Applications. Springer.Google Scholar
Joseph, D.D. & Renardy, Y.Y. 1992 b Fundamentals of Two-Fluid Dynamics. Volume 2: Lubricated Transport, Drops and Miscible Fluids. Springer.Google Scholar
Karpitschka, S., Liebig, F. & Riegler, H. 2017 Marangoni contraction of evaporating sessile droplets of binary mixtures. Langmuir 33, 4682–4687.CrossRefGoogle ScholarPubMed
Khenner, M. 2018 Modeling solid-state dewetting of a single-crystal binary alloy thin films. J. Appl. Phys. 123, 034302.CrossRefGoogle Scholar
Khenner, M. & Henner, V. 2020 Modeling evolution of composition patterns in a binary surface alloy. Model. Simul. Mater. Sci. Engng 29, 015002.CrossRefGoogle Scholar
Kondic, L., Gonzalez, A.G., Diez, J.A., Fowlkes, J.D. & Rack, P. 2020 Liquid-state dewetting of pulsed-laser-heated nanoscale metal films and other geometries. Annu. Rev. Fluid Mech. 52, 235–262.CrossRefGoogle Scholar
Köpf, M.H., Gurevich, S.V. & Friedrich, R. 2009 Thin film dynamics with surfactant phase transition. Europhys. Lett. 86, 66003.CrossRefGoogle Scholar
Köpf, M.H., Gurevich, S.V., Friedrich, R. & Chi, L. 2010 Pattern formation in monolayer transfer systems with substrate-medicated condensation. Langmuir 26, 10444–10447.CrossRefGoogle ScholarPubMed
Makarov, S.V., Milichko, V.A., Mukhin, I.S., Shishkin, I.I., Zuev, D.A., Mozharov, A.M., Krasnok, A.E. & Belov, P.A. 2016 Controllable femtosecond laser-induced dewetting for plasmonic applications. Laser Photonics Rev. 10, 91–93.CrossRefGoogle Scholar
Mao, S., Kuldinow, D., Haataja, M.P. & Kosmrlj, A. 2019 Phase behavior and morphology of multicomponent liquid mixtures. Soft Matt. 15, 1297–1311.CrossRefGoogle ScholarPubMed
Mitlin, V.S. 1993 Dewetting of solid surface: analogy with spinodal decomposition. J. Colloid Interface Sci. 156, 491–497.CrossRefGoogle Scholar
Morozov, M., Oron, A. & Nepomnyashchy, A.A. 2015 Long-wave Marangoni convection in a layer of surfactant solution: bifurcation analysis. Phys. Fluids 27, 082107.CrossRefGoogle Scholar
Náraigh, L.O. & Thiffeault, J-L. 2010 Nonlinear dynamics of phase separation in thin films. Nonlinearity 23, 1559–1583.CrossRefGoogle Scholar
Oron, A., Davis, S.H. & Bankoff, S.G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Parlett, I.B.N. 1998 The Symmetric Eigenvalue Problem. SIAM.CrossRefGoogle Scholar
Peters, G. & Wilkinson, J.H. 1970 $A x = \lambda B x$ and the generalized eigenproblem. SIAM J. Numer. Anal. 7, 479–492.CrossRefGoogle Scholar
Podolny, A., Oron, A. & Nepomnyashchy, A.A. 2005 Long-wave Marangoni instability in a binary-liquid layer with deformable interface in the presence of Soret effect: linear theory. Phys. Fluids 17, 104104.CrossRefGoogle Scholar
Pototsky, A., Bestehorn, M., Merkt, D. & Thiele, U. 2004 Alternative pathways of dewetting for a thin liquid two-layer film. Phys. Rev. E 70, 025201.CrossRefGoogle ScholarPubMed
Pototsky, A., Bestehorn, M., Merkt, D. & Thiele, U. 2005 Morphology changes in the evolution of liquid two-layer films. J. Chem. Phys. 122, 224711.CrossRefGoogle ScholarPubMed
Sarika, C.K., Tomar, G. & Basu, J.K. 2016 Pattern formation in thin films of polymer solutions: theory and simulations. J. Chem. Phys. 144, 024902.CrossRefGoogle Scholar
Sarika, C.K., Tomar, G., Basu, J.K. & Thiele, U. 2015 Bimodality and re-entrant behaviour in the hierarchical self-assembly of polymeric nanoparticles. Soft Matt. 11, 8975–8980.Google Scholar
Sharma, A. & Jameel, A.T. 1993 Nonlinear stability, rupture and morphological phase separation of thin fluid films on polar and polar substrates. J. Colloid Interface Sci. 161, 190–208.CrossRefGoogle Scholar
Sharma, A., Kishore, C.S., Salaniwal, S. & Ruckenstein, E. 1995 Nonlinear stability and rupture of ultrathin free films. Phys. Fluids 7, 1832–1840.CrossRefGoogle Scholar
Shklyaev, S., Nepomnyashchy, A.A. & Oron, A. 2009 Marangoni convection in a binary liquid layer with soret effect at small lewis number: linear stability analysis. Phys. Fluids 21, 054101.CrossRefGoogle Scholar
Shklyaev, S., Nepomnyashchy, A.A. & Oron, A. 2013 Oscillatory longwave marangoni convection in a binary liquid: rhombic patterns. SIAM J. Appl. Maths 73, 2203–2223.CrossRefGoogle Scholar
Shklyaev, S., Nepomnyashchy, A.A. & Oron, A. 2014 Oscillatory longwave Marangoni convection in a binary liquid. Part 2: square patterns. SIAM J. Appl. Maths 74, 1005–1024.CrossRefGoogle Scholar
Strang, G. 1988 Linear Algebra and Its Applications, 3rd edn. Harcourt Brace Jovanovich College Publishers.Google Scholar
Thiele, U. 2011 Note on thin film equations for solutions and suspensions. Eur. Phys. J. Spec. Top. 197, 213–220.CrossRefGoogle Scholar
Thiele, U. 2018 Recent advances in and future challenges for mesoscopic hydrodynamic modelling of complex wetting. Colloids Surf. A 553, 487–495.CrossRefGoogle Scholar
Thiele, U., Archer, A.J. & Pismen, L.M. 2016 Gradient dynamics models for liquid films with soluble surfactant. Phys. Rev. Fluids 1, 083903.CrossRefGoogle Scholar
Thiele, U., Archer, A.J. & Plapp, M. 2012 Thermodynamically consistent description of the hydrodynamics of free surfaces covered by insoluble surfactants of high concentration. Phys. Fluids 24, 102107.CrossRefGoogle Scholar
Thiele, U., Madruga, S. & Frastia, L. 2007 Decomposition driven interface evolution for layers of binary mixtures. I. Model derivation and stratified base states. Phys. Fluids 19, 122106.CrossRefGoogle Scholar
Thiele, U., Todorova, D.V. & Lopez, H. 2013 Gradient dynamics description for films of mixtures and suspensions: dewetting triggered by coupled film height and concentration fluctuations. Phys. Rev. Lett. 111, 117801.CrossRefGoogle ScholarPubMed
Thiele, U., Velarde, M.G. & Neuffer, K. 2001 Dewetting: film rupture by nucleation in the spinodal regime. Phys. Rev. Lett. 87, 016104.CrossRefGoogle ScholarPubMed
Thompson, C.V. 2012 Solid-state dewetting of thin films. Annu. Rev. Mater. Res. 42, 399–434.CrossRefGoogle Scholar
Todorova, D.V. 2013 Modelling of dynamical effects related to the wettability and capillarity of simple and complex liquids. PhD thesis, Loughborough University.Google Scholar
Xu, X., Thiele, U. & Qian, T. 2015 A variational approach to thin film hydrodynamics of binary mixtures. J. Phys.: Condens. Matter 27, 085005.Google ScholarPubMed