1. Introduction
Slender double wedges are commonly encountered in intakes, control surfaces and junctions in high-speed supersonic and hypersonic vehicles (Dolling Reference Dolling2001). In this geometry, a laminar boundary layer can separate at the corner because of the pressure rise that arises from deflection of the inviscid free stream. The resulting flow is characterized by separation–reattachment shocks as well as a recirculation zone and it provides a canonical set-up for studying shock-wave-boundary-layer interaction (SWBLI) (Simeonides & Haase Reference Simeonides and Haase1995). In spite of spanwise homogeneity of laminar base flows over compression corners, both experiments (Chuvakhov et al. Reference Chuvakhov, Borovoy, Egorov, Radchenko, Olivier and Roghelia2017; Roghelia et al. Reference Roghelia, Olivier, Egorov and Chuvakhov2017; Dwivedi et al. Reference Dwivedi, Broslawski, Candler and Bowersox2020a) and numerical simulations (Navarro-Martinez & Tutty Reference Navarro-Martinez and Tutty2005; Dwivedi et al. Reference Dwivedi, Nichols, Jovanović and Candler2017; Cao et al. Reference Cao, Hao, Klioutchnikov, Olivier and Wen2021b) identify three-dimensional (3-D) features in time-averaged separated flows. In particular, streamwise streaks associated with persistent local peaks of heat flux or wall temperature, that appear near reattachment, can trigger transition to turbulence downstream (Simeonides & Haase Reference Simeonides and Haase1995; Roghelia et al. Reference Roghelia, Olivier, Egorov and Chuvakhov2017).
The development of 3-D flow structures in hypersonic flows was recently studied by examining the growth of small perturbations in the presence of a recirculation zone (Dwivedi Reference Dwivedi2020). For example, two-dimensional (2-D) SWBLI can become unstable inside the separation bubble when the strength of interaction increases beyond a critical value (Sidharth et al. Reference Sidharth, Dwivedi, Candler and Nichols2017). The spanwise modulation that arises from global instability introduces streaks over compression corners (Sidharth et al. Reference Sidharth, Dwivedi, Candler and Nichols2018) as well as oblique shocks impinging on a flat plate (Hildebrand et al. Reference Hildebrand, Dwivedi, Nichols, Jovanović and Candler2018) and it can trigger transition to turbulence (Cao et al. Reference Cao, Hao, Klioutchnikov, Wen, Olivier and Heufer2022). Similar 3-D flow features have also been observed in hypersonic regimes where non-continuum effects are important (Sawant, Theofilis & Levin Reference Sawant, Theofilis and Levin2022). However, recent numerical simulations and global stability analysis demonstrate that hypersonic compression corner flows can be stabilized by increasing the radius of the leading edge (i.e. its bluntness) (Cao et al. Reference Cao, Hao, Klioutchnikov, Olivier, Heufer and Wen2021a) or by increasing the wall temperature (Hao et al. Reference Hao, Cao, Wen and Olivier2021).
Even in the absence of global instability, high-speed separated flows are highly sensitive to upstream vortical disturbances (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), and small fluctuations around the laminar 2-D base flow can experience significant non-modal amplification that leads to the appearance of steady reattachment streaks (Dwivedi et al. Reference Dwivedi, Hildebrand, Nichols, Candler and Jovanović2020b). Furthermore, recent experiments on the cone-flare configurations (Benitez et al. Reference Benitez, Esquieu, Jewell and Schneider2020; Butler & Laurence Reference Butler and Laurence2021), which represent axisymmetric counterparts of slender double wedges, identify unsteady fluctuations in the separation zone. These fluctuations are significantly amplified in the recirculation zone and they play an important role in transition to turbulence (Butler & Laurence Reference Butler and Laurence2021).
In this paper we examine amplification of unsteady fluctuations around the laminar 2-D base flow in the separation–reattachment zone and investigate subsequent transition to turbulence. Free-stream disturbances (Choudhari Reference Choudhari1996; Berlin & Henningson Reference Berlin and Henningson1999; Maslov et al. Reference Maslov, Shiplyuk, Sidorenko and Arnal2001) that arise from wind tunnel noise in ground experiments (Schneider Reference Schneider2015) or from atmospheric disturbances in free flights (Bushnell Reference Bushnell1990; Skinner et al. Reference Skinner, Butler, Laurence and Mangalam2020) can lead to the appearance of unsteady fluctuations in boundary layer flows. It is well documented that unsteady oblique waves provide a potent mechanism for initiating transition in low-speed incompressible (Berlin, Wiegel & Henningson Reference Berlin, Wiegel and Henningson1999; Rigas, Sipp & Colonius Reference Rigas, Sipp and Colonius2021) and compressible (Chang & Malik Reference Chang and Malik1994; Mayer, Von Terzi & Fasel Reference Mayer, Von Terzi and Fasel2011) boundary layers. Even though the importance of oblique fluctuations in initiating transition in attached high-speed boundary layers has received significant attention (Ma & Zhong Reference Ma and Zhong2005; Sivasubramanian & Fasel Reference Sivasubramanian and Fasel2015; Hader & Fasel Reference Hader and Fasel2019), their role in separated high-speed flows has not been studied. Recent experiments (Benitez et al. Reference Benitez, Esquieu, Jewell and Schneider2020) suggest that their amplification within the recirculation zone can trigger unsteadiness in transitional SBWLI flows. We utilize global resolvent and weakly nonlinear analyses to quantify amplification of unsteady upstream disturbances in a Mach ![]() $5$ flow over a slender double wedge, and characterize their role in initiating transition to turbulence in high-speed separated boundary layers.
$5$ flow over a slender double wedge, and characterize their role in initiating transition to turbulence in high-speed separated boundary layers.
Resolvent analysis provides a framework for evaluating responses (outputs) of stable dynamical systems to time-periodic external disturbances (inputs) (Trefethen et al. Reference Trefethen, Trefethen, Reddy and Driscoll1993; Schmid & Henningson Reference Schmid and Henningson2001; Schmid Reference Schmid2007). For time-independent globally stable base flows, the steady-state response of the linearized Navier–Stokes (NS) equations to a harmonic input with frequency ![]() $\omega$ is also harmonic with the same frequency and the frequency response operator maps the input forcing to the resulting steady-state output (Jovanović Reference Jovanović2021). The singular value decomposition (SVD) of the frequency response characterizes amplification across frequency
$\omega$ is also harmonic with the same frequency and the frequency response operator maps the input forcing to the resulting steady-state output (Jovanović Reference Jovanović2021). The singular value decomposition (SVD) of the frequency response characterizes amplification across frequency ![]() $\omega$ and decomposes inputs and outputs into modes whose significance is ordered by the magnitude of the corresponding singular values (Schmid Reference Schmid2007). In addition to providing insights into dynamics of canonical incompressible flows (Jovanović & Bamieh Reference Jovanović and Bamieh2005; McKeon & Sharma Reference McKeon and Sharma2010; Brandt et al. Reference Brandt, Sipp, Pralits and Marquet2011; Sipp & Marquet Reference Sipp and Marquet2013; Ran et al. Reference Ran, Zare, Hack and Jovanović2019a,Reference Ran, Zare, Hack and Jovanovićb), input–output analysis has also been utilized to discover mechanisms for noise generation in turbulent jets (Garnaud et al. Reference Garnaud, Lesshafft, Schmid and Huerre2013; Jeun, Nichols & Jovanović Reference Jeun, Nichols and Jovanović2016; Schmidt et al. Reference Schmidt, Towne, Rigas, Colonius and Brès2018), separation control on airfoils (Yeh & Taira Reference Yeh and Taira2019) and the appearance of reattachment streaks in hypersonic flows (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019).
$\omega$ and decomposes inputs and outputs into modes whose significance is ordered by the magnitude of the corresponding singular values (Schmid Reference Schmid2007). In addition to providing insights into dynamics of canonical incompressible flows (Jovanović & Bamieh Reference Jovanović and Bamieh2005; McKeon & Sharma Reference McKeon and Sharma2010; Brandt et al. Reference Brandt, Sipp, Pralits and Marquet2011; Sipp & Marquet Reference Sipp and Marquet2013; Ran et al. Reference Ran, Zare, Hack and Jovanović2019a,Reference Ran, Zare, Hack and Jovanovićb), input–output analysis has also been utilized to discover mechanisms for noise generation in turbulent jets (Garnaud et al. Reference Garnaud, Lesshafft, Schmid and Huerre2013; Jeun, Nichols & Jovanović Reference Jeun, Nichols and Jovanović2016; Schmidt et al. Reference Schmidt, Towne, Rigas, Colonius and Brès2018), separation control on airfoils (Yeh & Taira Reference Yeh and Taira2019) and the appearance of reattachment streaks in hypersonic flows (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019).
In a Mach ![]() $5$ double-wedge flow subject to unsteady disturbances, we employ resolvent analysis to demonstrate that oblique waves represent the most energetic response of the compressible linearized NS equations. We utilize the compressible energy norm (Chu Reference Chu1965; Hanifi, Schmid & Henningson Reference Hanifi, Schmid and Henningson1996) to quantify energy amplification and show that unsteady upstream disturbances that are localized before flow separation induce oblique waves downstream of the double-wedge corner. Our analysis of the transport equation for the streamwise specific kinetic energy of oblique waves reveals that concave flow curvature of the separated/reattaching laminar 2-D base flow is the primary source of amplification in the presence of SWBLI. We also utilize a weakly nonlinear analysis to demonstrate that quadratic interactions of oblique waves generate vortical excitations that induce reattachment streaks in the recirculation bubble. We show that the resolvent operator associated with linearization around the laminar 2-D base flow governs the evolution of steady reattachment streaks and use SVD to demonstrate that the streaks are well approximated by the second output resolvent mode. Our analysis of the energy budget shows that the base flow deceleration near reattachment is primarily responsible for amplification of reattachment streaks. Finally, we conduct direct numerical simulations (DNS) to confirm the predictive power of our approach and provide insight into latter stages of transition to turbulence.
$5$ double-wedge flow subject to unsteady disturbances, we employ resolvent analysis to demonstrate that oblique waves represent the most energetic response of the compressible linearized NS equations. We utilize the compressible energy norm (Chu Reference Chu1965; Hanifi, Schmid & Henningson Reference Hanifi, Schmid and Henningson1996) to quantify energy amplification and show that unsteady upstream disturbances that are localized before flow separation induce oblique waves downstream of the double-wedge corner. Our analysis of the transport equation for the streamwise specific kinetic energy of oblique waves reveals that concave flow curvature of the separated/reattaching laminar 2-D base flow is the primary source of amplification in the presence of SWBLI. We also utilize a weakly nonlinear analysis to demonstrate that quadratic interactions of oblique waves generate vortical excitations that induce reattachment streaks in the recirculation bubble. We show that the resolvent operator associated with linearization around the laminar 2-D base flow governs the evolution of steady reattachment streaks and use SVD to demonstrate that the streaks are well approximated by the second output resolvent mode. Our analysis of the energy budget shows that the base flow deceleration near reattachment is primarily responsible for amplification of reattachment streaks. Finally, we conduct direct numerical simulations (DNS) to confirm the predictive power of our approach and provide insight into latter stages of transition to turbulence.
Recently, Rigas et al. (Reference Rigas, Sipp and Colonius2021) utilized a variational framework to extend input–output analysis in the frequency domain to the nonlinear NS equations. For fundamental forcing, the disturbance that triggers transition and yields the largest skin-friction coefficient in an incompressible boundary layer is given by a pair of oblique waves with a temporal frequency and spanwise wavenumber which are very close to those identified by the resolvent analysis of the linearized NS equations (Rigas et al. Reference Rigas, Sipp and Colonius2021). While the Orr-mechanism (Schmid & Henningson Reference Schmid and Henningson2001) and the Tollmien–Schlichting linear instability (Sipp & Marquet Reference Sipp and Marquet2013) initiate the early stages of oblique transition in the attached low-speed boundary layers (Rigas et al. Reference Rigas, Sipp and Colonius2021), even linear amplification mechanisms are poorly understood in separated compressible flows. Recent numerical simulations with inlet stochastic excitations in axisymmetric cylinder flare geometry showed that the local ‘first mode’ instability (Mack Reference Mack1984) can cause growth of oblique waves in the upstream boundary layer (i.e. before separation) and initiate transition in high-speed compressible flows with SWBLI (Lugrin et al. Reference Lugrin, Beneddine, Leclercq, Garnier and Bur2021). However, in the absence of local and global boundary layer instabilities, the role of flow separation in the amplification of unsteady fluctuations and the ensuing transition has not been previously investigated.
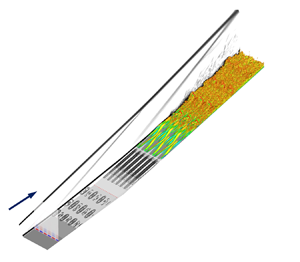
Figure 1 provides a summary of our key findings. We utilize resolvent analysis of the laminar 2-D base flow with spatially localized forcing introduced in the streamwise plane immediately upstream of separation to identify the spatial structure of unsteady external disturbances that yield the most energetic response of the compressible linearized NS equations. The resulting forcing is used to trigger non-modal amplification of oblique waves in the separated shear layer and generate steady reattachment streaks, which are routinely observed in SWBLI experiments, further downstream through weakly nonlinear interactions. Interaction of streaks with oblique waves is observed after reattachment and DNS is used to demonstrate that unsteady upstream oblique disturbances can indeed trigger transition to turbulence in separated high-speed compressible flows.

Figure 1. Preview of key results: spatially localized unsteady upstream forcing triggers oblique waves in the separated shear layer and their quadratic interactions lead to the appearance of steady reattachment streaks further downstream. Direct numerical simulation validates our theoretical predictions and demonstrates the efficacy of unsteady oblique disturbances in triggering transition in globally stable separated high-speed boundary layer flows.
Our presentation is organized as follows. In § 2 we introduce the slender double-wedge geometry along with a finite-volume compressible flow solver that we use in our computations. In § 3 we describe resolvent and weakly nonlinear analyses that we use to evaluate frequency responses of the double-wedge flow in the presence of 3-D disturbances. We also utilize resolvent analysis to demonstrate the large amplification of unsteady oblique disturbances to the linearized flow equations and identify the underlying physical mechanism. In § 4 we employ a weakly nonlinear analysis to demonstrate that quadratic interactions of oblique waves induce steady reattachment streaks and discuss the physical mechanism responsible for their amplification in the recirculation zone. In § 5 we employ DNS to validate utility of our theoretical predictions and examine latter stages of transition induced by unsteady upstream disturbances. In § 6 we analyse statistical features of the resulting transitional and turbulent boundary layers. We provide a summary of our contributions and offer concluding remarks in § 7.
2. Hypersonic flow over an adiabatic slender double wedge
Hypersonic flow over a slender double wedge with free-stream conditions shown in figure 2 corresponds to the experiments of Yang et al. (Reference Yang, Zare-Behtash, Erdem and Kontis2012). Since the enthalpy and the temperature in the flow field are low, we utilize the ideal gas law abstraction and employ the finite-volume compressible flow solver US3D (Candler et al. Reference Candler, Johnson, Nompelis, Gidzak, Subbareddy and Barnhardt2015a) to compute the solution of the compressible NS equations in conservative form,
Here, ![]() $\mathcal {F} ({\boldsymbol {\varPsi }}) \mathrel {\mathop :}= - \boldsymbol {\nabla } \boldsymbol {\cdot } {\boldsymbol{F}} ({\boldsymbol {\varPsi }})$ is the dynamical generator of the compressible NS equations,
$\mathcal {F} ({\boldsymbol {\varPsi }}) \mathrel {\mathop :}= - \boldsymbol {\nabla } \boldsymbol {\cdot } {\boldsymbol{F}} ({\boldsymbol {\varPsi }})$ is the dynamical generator of the compressible NS equations, ![]() ${\boldsymbol{F}} ({\boldsymbol {\varPsi }})$ is the flux vector,
${\boldsymbol{F}} ({\boldsymbol {\varPsi }})$ is the flux vector, ![]() $\boldsymbol {\nabla }$ is the gradient and
$\boldsymbol {\nabla }$ is the gradient and ![]() ${\boldsymbol {\varPsi }} = (\rho, \rho \boldsymbol{u}, E_t)$ is the vector of conserved variables that represent density, momentum and total energy per unit volume of the gas. In (2.1) and throughout the paper, spatial coordinates are non-dimensionalized by the boundary layer thickness at separation
${\boldsymbol {\varPsi }} = (\rho, \rho \boldsymbol{u}, E_t)$ is the vector of conserved variables that represent density, momentum and total energy per unit volume of the gas. In (2.1) and throughout the paper, spatial coordinates are non-dimensionalized by the boundary layer thickness at separation ![]() $\delta _{99} = 9.8 \times 10^{-4} \, \mathrm {m}$, velocity by the free-stream velocity
$\delta _{99} = 9.8 \times 10^{-4} \, \mathrm {m}$, velocity by the free-stream velocity ![]() $U_\infty$, pressure by
$U_\infty$, pressure by ![]() $p_{\infty }$, temperature by
$p_{\infty }$, temperature by ![]() $T_{\infty }$ and time by
$T_{\infty }$ and time by ![]() $\delta _{99}/U_\infty$. The Reynolds number based on the separation boundary layer thickness is
$\delta _{99}/U_\infty$. The Reynolds number based on the separation boundary layer thickness is ![]() $13.3 \times 10 ^{3}$ and the Mach number is
$13.3 \times 10 ^{3}$ and the Mach number is ![]() $5.0$.
$5.0$.

Figure 2. Slender double-wedge geometry and the associated free-stream conditions.
We discretize the inviscid fluxes using the second-order accurate modified Steger–Warming fluxes with the MUSCL limiters (Candler et al. Reference Candler, Johnson, Nompelis, Gidzak, Subbareddy and Barnhardt2015a). In previous studies, the numerical method for the computation of the base state was validated using hypersonic double-wedge and double-cone set-ups (Nompelis, Candler & Holden Reference Nompelis, Candler and Holden2003; Nompelis & Candler Reference Nompelis and Candler2009). The laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$ is computed as the steady-state solution of (2.1),
$\bar {{\boldsymbol {\varPsi }}}$ is computed as the steady-state solution of (2.1),
by implicit time marching with 249 cells in the normal direction and 535 cells in the streamwise direction. As illustrated in Sidharth et al. (Reference Sidharth, Dwivedi, Candler and Nichols2018), this resolution is sufficient to capture separated flow and resolve the evolution of small perturbations.
Figure 3 shows the contours of the density gradient magnitude on the compression corner. The separation and the reattachment locations in the laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$ are marked by S and R, respectively. The 2-D flow separates upstream of the corner on the first wedge, it reattaches on the second wedge, and the separated and reattaching shear layers are respectively associated with the formation of the separation and reattachment shocks. Figure 3 also shows an inset of the separation zone along with the wall-aligned coordinate system (where
$\bar {{\boldsymbol {\varPsi }}}$ are marked by S and R, respectively. The 2-D flow separates upstream of the corner on the first wedge, it reattaches on the second wedge, and the separated and reattaching shear layers are respectively associated with the formation of the separation and reattachment shocks. Figure 3 also shows an inset of the separation zone along with the wall-aligned coordinate system (where ![]() $\xi$ and
$\xi$ and ![]() $\eta$ denote directions that are parallel and perpendicular to the wall) and a coordinate system that is locally aligned with the streamlines of the laminar 2-D flow. Both coordinate systems are used in our study of the evolution of flow fluctuations.
$\eta$ denote directions that are parallel and perpendicular to the wall) and a coordinate system that is locally aligned with the streamlines of the laminar 2-D flow. Both coordinate systems are used in our study of the evolution of flow fluctuations.

Figure 3. Contours of density gradient magnitude. The inset shows a zoomed in view of the separation bubble and the schematic shows various coordinate systems associated with the double-wedge geometry.
Sidharth et al. (Reference Sidharth, Dwivedi, Candler and Nichols2018) demonstrated global linear stability of the laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$. Recent studies of similar SWBLI configurations, such as compression ramps, revealed extreme sensitivity to upstream disturbances even in the absence of global instability (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019). Leading-edge roughness and free-stream disturbances provide persistent sources of external excitation and they are inevitable in realistic flows. To evaluate the role of such uncertainty in triggering early stages of transition to turbulence, we utilize input–output analysis to quantify amplification of unsteady disturbances in a hypersonic flow over a slender double wedge.
$\bar {{\boldsymbol {\varPsi }}}$. Recent studies of similar SWBLI configurations, such as compression ramps, revealed extreme sensitivity to upstream disturbances even in the absence of global instability (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019). Leading-edge roughness and free-stream disturbances provide persistent sources of external excitation and they are inevitable in realistic flows. To evaluate the role of such uncertainty in triggering early stages of transition to turbulence, we utilize input–output analysis to quantify amplification of unsteady disturbances in a hypersonic flow over a slender double wedge.
3. Input–output analysis of a high-speed double-wedge flow
In this section we employ input–output analysis to quantify amplification of small unsteady external disturbances in globally stable 2-D SWBLI over a slender double wedge, and uncover physical mechanisms that trigger early stages of transition to turbulence.
3.1. Externally forced compressible NS equations
To account for the rate of change of perturbation density, momentum and total energy, we model unsteady external disturbances ![]() $\boldsymbol {{d}}(\boldsymbol{x}, t)$ to the compressible NS equations in the conservative form (2.1) as volumetric sources of excitation,
$\boldsymbol {{d}}(\boldsymbol{x}, t)$ to the compressible NS equations in the conservative form (2.1) as volumetric sources of excitation,
where ![]() $\boldsymbol{x} \mathrel {\mathop :}= (x,y,z)$ is the vector of streamwise, normal and spanwise spatial coordinates. By decomposing the flow field
$\boldsymbol{x} \mathrel {\mathop :}= (x,y,z)$ is the vector of streamwise, normal and spanwise spatial coordinates. By decomposing the flow field ![]() ${\boldsymbol {\varPsi }}$ into the sum of the base
${\boldsymbol {\varPsi }}$ into the sum of the base ![]() $\bar {{\boldsymbol {\varPsi }}}$ and fluctuating
$\bar {{\boldsymbol {\varPsi }}}$ and fluctuating ![]() ${\boldsymbol {\psi }}$ parts,
${\boldsymbol {\psi }}$ parts,
we obtain the equation that governs the dynamics of flow fluctuations around ![]() $\bar {{\boldsymbol {\varPsi }}} (\boldsymbol{x})$,
$\bar {{\boldsymbol {\varPsi }}} (\boldsymbol{x})$,
For disturbances with small amplitude ![]() $\epsilon$,
$\epsilon$,
a weakly nonlinear analysis can be utilized to examine externally forced compressible NS equations (3.3) and determine the corrections to the steady laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}} (\boldsymbol{x})$. Up to a second order in
$\bar {{\boldsymbol {\varPsi }}} (\boldsymbol{x})$. Up to a second order in ![]() $\epsilon$, the vector of flow fluctuations
$\epsilon$, the vector of flow fluctuations ![]() ${\boldsymbol {\psi }}$ can be represented as
${\boldsymbol {\psi }}$ can be represented as
where ![]() ${\boldsymbol {\psi }}^{(1)}(\boldsymbol{x}, t)$ satisfies the linearized flow equations
${\boldsymbol {\psi }}^{(1)}(\boldsymbol{x}, t)$ satisfies the linearized flow equations
and ![]() ${\boldsymbol {\psi }}^{(2)}(\boldsymbol{x}, t)$ satisfies
${\boldsymbol {\psi }}^{(2)}(\boldsymbol{x}, t)$ satisfies
Equations (3.5a) and (3.5b) are respectively obtained by neglecting ![]() $O (\epsilon ^2)$ and
$O (\epsilon ^2)$ and ![]() $O (\epsilon ^3)$ terms upon substitution of (3.4a) and (3.4b) to the compressible NS equations (3.3). The compressible NS operator resulting from linearization around the base flow
$O (\epsilon ^3)$ terms upon substitution of (3.4a) and (3.4b) to the compressible NS equations (3.3). The compressible NS operator resulting from linearization around the base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$ is determined by
$\bar {{\boldsymbol {\varPsi }}}$ is determined by ![]() $\mathcal {A} (\bar {{\boldsymbol {\varPsi }}})$ (see Candler, Subbareddy & Nompelis (Reference Candler, Subbareddy and Nompelis2015b, equation (23)) and Sidharth et al. (Reference Sidharth, Dwivedi, Candler and Nichols2018, equations (A1)–(A2))) and
$\mathcal {A} (\bar {{\boldsymbol {\varPsi }}})$ (see Candler, Subbareddy & Nompelis (Reference Candler, Subbareddy and Nompelis2015b, equation (23)) and Sidharth et al. (Reference Sidharth, Dwivedi, Candler and Nichols2018, equations (A1)–(A2))) and ![]() $\mathcal {N}^{(2)} ( {\boldsymbol {\psi }}^{(1)} )$ accounts for quadratic interactions at
$\mathcal {N}^{(2)} ( {\boldsymbol {\psi }}^{(1)} )$ accounts for quadratic interactions at ![]() $O (\epsilon ^2)$; see Appendix A for details.
$O (\epsilon ^2)$; see Appendix A for details.
Several recent studies demonstrated the utility of the compressible energy norm (Chu Reference Chu1965; Hanifi et al. Reference Hanifi, Schmid and Henningson1996),
in quantifying the growth of fluctuations in high-speed boundary layer flows (Franko & Lele Reference Franko and Lele2013; Sidharth et al. Reference Sidharth, Dwivedi, Candler and Nichols2018; Quintanilha et al. Reference Quintanilha, Paredes, Hanifi and Theofilis2022). This quantity is determined by the weighted ![]() $L_2$ norm of the vector of flow fluctuations
$L_2$ norm of the vector of flow fluctuations ![]() ${\boldsymbol {\phi }} \mathrel {\mathop :}= (\phi _{1}, {\boldsymbol {\phi }}_{2}, \phi _{3}) = (\rho ^\prime, \boldsymbol {u}^\prime, T^\prime )$ in primitive variables,
${\boldsymbol {\phi }} \mathrel {\mathop :}= (\phi _{1}, {\boldsymbol {\phi }}_{2}, \phi _{3}) = (\rho ^\prime, \boldsymbol {u}^\prime, T^\prime )$ in primitive variables,
where ![]() $\langle\, {\cdot }\, , \,{\cdot }\, \rangle _2$ is the standard
$\langle\, {\cdot }\, , \,{\cdot }\, \rangle _2$ is the standard ![]() $L_2$ inner product over the domain
$L_2$ inner product over the domain ![]() $\varOmega$,
$\varOmega$, ![]() $C_{v}$ is the specific heat at constant volume in
$C_{v}$ is the specific heat at constant volume in ![]() $\varOmega$ and
$\varOmega$ and
 \begin{equation} {\mathcal{W} \; \mathrel{\mathop:}= \; \dfrac{1}{2} \left[ \begin{array}{ccc} \bar{p} / \bar{\rho}^{2} & 0 & 0 \\ 0 & \bar{\rho} & 0 \\ 0 & 0 & C_{v} \bar{\rho}/\bar{T} \end{array} \right]} \end{equation}
\begin{equation} {\mathcal{W} \; \mathrel{\mathop:}= \; \dfrac{1}{2} \left[ \begin{array}{ccc} \bar{p} / \bar{\rho}^{2} & 0 & 0 \\ 0 & \bar{\rho} & 0 \\ 0 & 0 & C_{v} \bar{\rho}/\bar{T} \end{array} \right]} \end{equation}
is the multiplication operator determined by the pressure ![]() $\bar {p}$, density
$\bar {p}$, density ![]() $\bar {\rho }$ and temperature
$\bar {\rho }$ and temperature ![]() $\bar {T}$ of the base flow
$\bar {T}$ of the base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$. For small amplitude disturbances, we can represent
$\bar {{\boldsymbol {\varPsi }}}$. For small amplitude disturbances, we can represent ![]() ${\boldsymbol {\phi }}$ as
${\boldsymbol {\phi }}$ as
where
 \begin{equation} \left. \begin{gathered} {\boldsymbol{\phi}}^{(1)}(\boldsymbol{x}, t) = \mathcal{C} \, {\boldsymbol{\psi}}^{(1)}(\boldsymbol{x}, t),\\ {\boldsymbol{\phi}}^{(2)}(\boldsymbol{x}, t) = \mathcal{C} \, {\boldsymbol{\psi}}^{(2)}(\boldsymbol{x}, t) + \mathcal{D} \left[ \begin{array}{c} -{\phi^{(1)}_{1}} {{\boldsymbol{\phi}}^{(1)}_{2}} \\ -2 C_{v} {\phi^{(1)}_{1}} {\phi^{(1)}_{3}} - \bar{\varPhi}_{1} |{{\boldsymbol{\phi}}^{(1)}_{2}}|^{2} \end{array} \right]. \end{gathered} \right\} \end{equation}
\begin{equation} \left. \begin{gathered} {\boldsymbol{\phi}}^{(1)}(\boldsymbol{x}, t) = \mathcal{C} \, {\boldsymbol{\psi}}^{(1)}(\boldsymbol{x}, t),\\ {\boldsymbol{\phi}}^{(2)}(\boldsymbol{x}, t) = \mathcal{C} \, {\boldsymbol{\psi}}^{(2)}(\boldsymbol{x}, t) + \mathcal{D} \left[ \begin{array}{c} -{\phi^{(1)}_{1}} {{\boldsymbol{\phi}}^{(1)}_{2}} \\ -2 C_{v} {\phi^{(1)}_{1}} {\phi^{(1)}_{3}} - \bar{\varPhi}_{1} |{{\boldsymbol{\phi}}^{(1)}_{2}}|^{2} \end{array} \right]. \end{gathered} \right\} \end{equation}
As shown in Appendix B, ![]() $\mathcal {C}$ and
$\mathcal {C}$ and ![]() $\mathcal {D}$ are multiplication operators parameterized by the laminar 2-D base flow
$\mathcal {D}$ are multiplication operators parameterized by the laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$; see (B4) for their definition.
$\bar {{\boldsymbol {\varPsi }}}$; see (B4) for their definition.
In the remainder of this section, we identify oblique waves as the most energetic responses of the linearized flow equations (3.5a) in the presence of unsteady harmonic disturbances ![]() $\boldsymbol {{d}}^{(1)}$. In § 4 we utilize (3.5b) to demonstrate that steady streaks can arise from quadratic interactions of unsteady oblique waves.
$\boldsymbol {{d}}^{(1)}$. In § 4 we utilize (3.5b) to demonstrate that steady streaks can arise from quadratic interactions of unsteady oblique waves.
3.2. Amplification of exogenous disturbances to the linearized flow equations
The linearized equations (3.5a) describe the evolution of the fluctuation vector ![]() ${\boldsymbol {\psi }}^{(1)}$ in the presence of external disturbances
${\boldsymbol {\psi }}^{(1)}$ in the presence of external disturbances ![]() $\boldsymbol {d}^{(1)}$ and they can be written using the state-space formulation (Schmid & Henningson Reference Schmid and Henningson2001)
$\boldsymbol {d}^{(1)}$ and they can be written using the state-space formulation (Schmid & Henningson Reference Schmid and Henningson2001)
 \begin{equation} \left. \begin{aligned} \frac{\partial {\boldsymbol{\psi}}^{(1)}}{\partial t} & = \mathcal{A} {\boldsymbol{\psi}}^{(1)} + \mathcal{B} \boldsymbol{d}^{(1)}, \\ {\boldsymbol{\phi}}^{(1)} & = \mathcal{C} {\boldsymbol{\psi}}^{(1)}. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \frac{\partial {\boldsymbol{\psi}}^{(1)}}{\partial t} & = \mathcal{A} {\boldsymbol{\psi}}^{(1)} + \mathcal{B} \boldsymbol{d}^{(1)}, \\ {\boldsymbol{\phi}}^{(1)} & = \mathcal{C} {\boldsymbol{\psi}}^{(1)}. \end{aligned} \right\} \end{equation}
Here, ![]() $\boldsymbol {d}^{(1)}$ is a spatially distributed and temporally varying disturbance (input),
$\boldsymbol {d}^{(1)}$ is a spatially distributed and temporally varying disturbance (input), ![]() ${\boldsymbol {\psi }}^{(1)}$ is the state of the linearized system (which is determined by the vector of flow fluctuations in conserved variables),
${\boldsymbol {\psi }}^{(1)}$ is the state of the linearized system (which is determined by the vector of flow fluctuations in conserved variables), ![]() ${\boldsymbol {\phi }}^{(1)}$ is the quantity of interest (output) whose weighted
${\boldsymbol {\phi }}^{(1)}$ is the quantity of interest (output) whose weighted ![]() $L_2$ norm determines the energy of flow fluctuations (3.6) and
$L_2$ norm determines the energy of flow fluctuations (3.6) and ![]() $\mathcal {A}$ is the generator of the linearized compressible NS dynamics. The input operator
$\mathcal {A}$ is the generator of the linearized compressible NS dynamics. The input operator ![]() $\mathcal {B}$ in (3.8) allows us to specify spatial support of body forcing inputs, and the output operator
$\mathcal {B}$ in (3.8) allows us to specify spatial support of body forcing inputs, and the output operator ![]() $\mathcal {C}$ relates the state of the linearized system
$\mathcal {C}$ relates the state of the linearized system ![]() ${\boldsymbol {\psi }}^{(1)}$ to the vector of flow fluctuations in primitive variables
${\boldsymbol {\psi }}^{(1)}$ to the vector of flow fluctuations in primitive variables ![]() ${\boldsymbol {\phi }}^{(1)}$.
${\boldsymbol {\phi }}^{(1)}$.
For the parameters shown in figure 2, the linearized system is globally stable and for a time-periodic input with frequency ![]() $\omega$,
$\omega$, ![]() $\boldsymbol {d}^{(1)} (\boldsymbol {x}, t) = \hat {\boldsymbol{d}}^{(1)} (\boldsymbol {x}, \omega ) \mathrm {e}^{\mathrm {i} \omega t}$, the steady-state output of (3.8) is determined by
$\boldsymbol {d}^{(1)} (\boldsymbol {x}, t) = \hat {\boldsymbol{d}}^{(1)} (\boldsymbol {x}, \omega ) \mathrm {e}^{\mathrm {i} \omega t}$, the steady-state output of (3.8) is determined by ![]() ${\boldsymbol {\phi }}^{(1)} (\boldsymbol {x},t) = \hat {{\boldsymbol {\phi }}}^{(1)} (\boldsymbol {x}, \omega ) \mathrm {e}^{\mathrm {i} \omega t}$, where
${\boldsymbol {\phi }}^{(1)} (\boldsymbol {x},t) = \hat {{\boldsymbol {\phi }}}^{(1)} (\boldsymbol {x}, \omega ) \mathrm {e}^{\mathrm {i} \omega t}$, where
![]() $\mathcal {H} (\omega )$ is the frequency response operator,
$\mathcal {H} (\omega )$ is the frequency response operator,
and ![]() $\mathcal {R} (\omega ) = (\mathrm {i} \omega \mathcal {I} - \mathcal {A})^{-1}$ is the resolvent operator associated with the linearized model (3.8). At any
$\mathcal {R} (\omega ) = (\mathrm {i} \omega \mathcal {I} - \mathcal {A})^{-1}$ is the resolvent operator associated with the linearized model (3.8). At any ![]() $\omega$, the SVD of
$\omega$, the SVD of ![]() $\mathcal {H} (\omega )$ can be used to quantify amplification of time-periodic inputs (Jovanović Reference Jovanović2004; Schmid Reference Schmid2007; Jovanović Reference Jovanović2021),
$\mathcal {H} (\omega )$ can be used to quantify amplification of time-periodic inputs (Jovanović Reference Jovanović2004; Schmid Reference Schmid2007; Jovanović Reference Jovanović2021),
where ![]() $\sigma _i (\omega )$ denotes the
$\sigma _i (\omega )$ denotes the ![]() $i$th singular value of
$i$th singular value of ![]() $\mathcal {H} (\omega )$,
$\mathcal {H} (\omega )$, ![]() $\langle \,{\cdot }\, , \,{\cdot }\, \rangle _E$ is the inner product in (3.6) that induces the compressible energy norm, and
$\langle \,{\cdot }\, , \,{\cdot }\, \rangle _E$ is the inner product in (3.6) that induces the compressible energy norm, and ![]() $\boldsymbol {d}_{i} (\boldsymbol {x}, \omega )$ and
$\boldsymbol {d}_{i} (\boldsymbol {x}, \omega )$ and ![]() ${\boldsymbol {\phi }}_{i} (\boldsymbol {x}, \omega )$ are the left and right singular functions of
${\boldsymbol {\phi }}_{i} (\boldsymbol {x}, \omega )$ are the left and right singular functions of ![]() $\mathcal {H} (\omega )$ that provide orthonormal bases of the corresponding input and output spaces (with respect to
$\mathcal {H} (\omega )$ that provide orthonormal bases of the corresponding input and output spaces (with respect to ![]() $\langle \,{\cdot }\, , \,{\cdot }\, \rangle _E$).
$\langle \,{\cdot }\, , \,{\cdot }\, \rangle _E$).
The frequency response operator ![]() $\mathcal {H} (\omega )$ maps the
$\mathcal {H} (\omega )$ maps the ![]() $i$th input mode
$i$th input mode ![]() $\boldsymbol {d}_{i} (\boldsymbol {x}, \omega )$ into the response whose spatial profile is specified by the
$\boldsymbol {d}_{i} (\boldsymbol {x}, \omega )$ into the response whose spatial profile is specified by the ![]() $i$th output mode
$i$th output mode ![]() ${\boldsymbol {\phi }}_{i} (\boldsymbol {x}, \omega )$ and the amplification is determined by the corresponding singular value
${\boldsymbol {\phi }}_{i} (\boldsymbol {x}, \omega )$ and the amplification is determined by the corresponding singular value ![]() $\sigma _{i} (\omega )$. In other words, for
$\sigma _{i} (\omega )$. In other words, for
and ![]() $\| \hat {{\boldsymbol {\phi }}}^{(1)} ( \,{\cdot }\, , \omega ) \|_{E} = \sigma _i (\omega )$. Note that, at any
$\| \hat {{\boldsymbol {\phi }}}^{(1)} ( \,{\cdot }\, , \omega ) \|_{E} = \sigma _i (\omega )$. Note that, at any ![]() $\omega$,
$\omega$,
determines the largest induced gain with respect to a compressible energy norm, where (![]() $\boldsymbol {d}_1 (\boldsymbol {x}, \omega ),{\boldsymbol {\phi }}_1 (\boldsymbol {x}, \omega )$) identify the spatial structure of the dominant input–output pair. We use a second-order central finite-volume discretization (Sidharth et al. Reference Sidharth, Dwivedi, Candler and Nichols2018) to obtain a finite-dimensional approximation of the linearized model (3.8) and employ matrix-free Arnoldi iterations (Jeun et al. Reference Jeun, Nichols and Jovanović2016; Dwivedi Reference Dwivedi2020) to compute the singular values
$\boldsymbol {d}_1 (\boldsymbol {x}, \omega ),{\boldsymbol {\phi }}_1 (\boldsymbol {x}, \omega )$) identify the spatial structure of the dominant input–output pair. We use a second-order central finite-volume discretization (Sidharth et al. Reference Sidharth, Dwivedi, Candler and Nichols2018) to obtain a finite-dimensional approximation of the linearized model (3.8) and employ matrix-free Arnoldi iterations (Jeun et al. Reference Jeun, Nichols and Jovanović2016; Dwivedi Reference Dwivedi2020) to compute the singular values ![]() $\sigma _i (\omega )$ of
$\sigma _i (\omega )$ of ![]() $\mathcal {H} (\omega )$.
$\mathcal {H} (\omega )$.
3.3. Frequency response analysis
We utilize the resolvent analysis to study amplification of harmonic disturbances with frequency ![]() $\omega$ to the linearized flow equations. In double-wedge geometry the laminar 2-D base flow
$\omega$ to the linearized flow equations. In double-wedge geometry the laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$ is a function of streamwise normal coordinates,
$\bar {{\boldsymbol {\varPsi }}}$ is a function of streamwise normal coordinates, ![]() $\bar {{\boldsymbol {\varPsi }}} (x,y)$, and owing to homogeneity in the spanwise direction, the 3-D fluctuations in (3.5a) take the form
$\bar {{\boldsymbol {\varPsi }}} (x,y)$, and owing to homogeneity in the spanwise direction, the 3-D fluctuations in (3.5a) take the form
where ![]() $\beta =2{\rm \pi} /\lambda _z$ is the spanwise wavenumber. Thus, in addition to
$\beta =2{\rm \pi} /\lambda _z$ is the spanwise wavenumber. Thus, in addition to ![]() $\omega$, the frequency response operator is also parameterized by
$\omega$, the frequency response operator is also parameterized by ![]() $\beta$,
$\beta$,
where ![]() $\mathcal {A}_\beta$ denotes the Fourier symbol of the operator
$\mathcal {A}_\beta$ denotes the Fourier symbol of the operator ![]() $\mathcal {A}$ in (3.8) obtained by replacing the spanwise differential operator
$\mathcal {A}$ in (3.8) obtained by replacing the spanwise differential operator ![]() $\partial _z$ with
$\partial _z$ with ![]() $\mathrm {i} \beta$. At any pair
$\mathrm {i} \beta$. At any pair ![]() $(\omega, \beta )$,
$(\omega, \beta )$, ![]() $\mathcal {H}_\beta (\omega )$ maps the input function
$\mathcal {H}_\beta (\omega )$ maps the input function ![]() $\hat {\boldsymbol {d}}^{(1)}$ of
$\hat {\boldsymbol {d}}^{(1)}$ of ![]() $x$ and
$x$ and ![]() $y$ into the output function
$y$ into the output function ![]() $\hat {{\boldsymbol {\phi }}}^{(1)}$ of
$\hat {{\boldsymbol {\phi }}}^{(1)}$ of ![]() $x$ and
$x$ and ![]() $y$,
$y$,
and SVD of ![]() $\mathcal {H}_\beta (\omega )$ can be used to study amplification across spatio-temporal frequencies.
$\mathcal {H}_\beta (\omega )$ can be used to study amplification across spatio-temporal frequencies.
We first set ![]() ${\mathcal {B}} = {\mathcal {I}}$, i.e. we introduce body forcing inputs to excite flow at every spatial location in the computational domain
${\mathcal {B}} = {\mathcal {I}}$, i.e. we introduce body forcing inputs to excite flow at every spatial location in the computational domain ![]() $\varOmega$ and we choose the output operator
$\varOmega$ and we choose the output operator ![]() ${\mathcal {C}}$ to examine the impact of forcing on the compressible energy norm of
${\mathcal {C}}$ to examine the impact of forcing on the compressible energy norm of ![]() ${\boldsymbol {\phi }}^{(1)}$ in the entire
${\boldsymbol {\phi }}^{(1)}$ in the entire ![]() $\varOmega$. The resolvent analysis is done using a resolution that yields grid-independent outputs with
$\varOmega$. The resolvent analysis is done using a resolution that yields grid-independent outputs with ![]() $545$ cells in the streamwise direction,
$545$ cells in the streamwise direction, ![]() $249$ cells in the normal direction, and numerical sponge boundary conditions near the leading edge (
$249$ cells in the normal direction, and numerical sponge boundary conditions near the leading edge (![]() $x=1$) with the outflow boundaries are utilized.
$x=1$) with the outflow boundaries are utilized.
Figure 4 shows the dependence of the input–output gain ![]() $G(\omega,\lambda _z)$ on the frequency
$G(\omega,\lambda _z)$ on the frequency ![]() $\omega$ and the wavelength
$\omega$ and the wavelength ![]() $\lambda _z$. There are two major amplification regions with the respective peaks at
$\lambda _z$. There are two major amplification regions with the respective peaks at ![]() $(\omega =0,\lambda _{z}=1.5)$ and
$(\omega =0,\lambda _{z}=1.5)$ and ![]() $(\omega =0.4,\lambda _{z}=3)$. The first peak in
$(\omega =0.4,\lambda _{z}=3)$. The first peak in ![]() $G$ identifies the largest amplification and the corresponding output is determined by reattachment streaks that result from steady vortical disturbances upstream of the recirculation zone. We observe selective amplification of disturbances with
$G$ identifies the largest amplification and the corresponding output is determined by reattachment streaks that result from steady vortical disturbances upstream of the recirculation zone. We observe selective amplification of disturbances with ![]() $\lambda _z \approx 1.5$ and low-pass filtering features over
$\lambda _z \approx 1.5$ and low-pass filtering features over ![]() $\omega$. The gain
$\omega$. The gain ![]() $G$ experiences rapid decay beyond the roll-off frequency
$G$ experiences rapid decay beyond the roll-off frequency ![]() $\omega \approx 0.4$ and it attains its largest value at
$\omega \approx 0.4$ and it attains its largest value at ![]() $\omega =0$ for
$\omega =0$ for ![]() $\lambda _z$ that scales with the reattaching shear layer thickness (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019). In contrast to Dwivedi et al. (Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), which focused on disturbances with
$\lambda _z$ that scales with the reattaching shear layer thickness (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019). In contrast to Dwivedi et al. (Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), which focused on disturbances with ![]() $\omega = 0$, we examine unsteady disturbances that trigger oblique waves in the reattaching shear layer, as identified by the second peak in
$\omega = 0$, we examine unsteady disturbances that trigger oblique waves in the reattaching shear layer, as identified by the second peak in ![]() $G$. This amplification region takes place in a narrow band of temporal frequencies
$G$. This amplification region takes place in a narrow band of temporal frequencies ![]() $\omega$ over a fairly broad range of spanwise wavelengths
$\omega$ over a fairly broad range of spanwise wavelengths ![]() $\lambda _{z}$.
$\lambda _{z}$.

Figure 4. (a) Input–output gain ![]() $G (\omega,\lambda _z)$ associated with the resolvent operator across temporal frequency
$G (\omega,\lambda _z)$ associated with the resolvent operator across temporal frequency ![]() $\omega$ and spanwise wavelength
$\omega$ and spanwise wavelength ![]() $\lambda _z$. (b) Isosurfaces of streamwise vorticity and density fluctuations corresponding to the input–output modes
$\lambda _z$. (b) Isosurfaces of streamwise vorticity and density fluctuations corresponding to the input–output modes ![]() $\boldsymbol {d}_{1}$ and
$\boldsymbol {d}_{1}$ and ![]() ${\boldsymbol {\phi }}_1$.
${\boldsymbol {\phi }}_1$.
As demonstrated in figure 4, even when we allow disturbances to enter through the entire computational domain the largest amplification is caused by inputs that are localized upstream of the corner and the resulting response is localized downstream of the corner. The upstream disturbances are the most effective way to excite the flow because of the large convection velocity of the laminar 2-D base flow (Chomaz Reference Chomaz2005; Schmid Reference Schmid2007) and the dominant output emerges in the separated and reattached regions.
Experimental studies of oblique transition in channel and boundary layer flows (Elofsson & Alfredsson Reference Elofsson and Alfredsson1998; Berlin & Henningson Reference Berlin and Henningson1999) often utilize streamwise localized disturbances and a common criticism of the resolvent analysis is that the identified global input modes represent excitation sources that are not easy to realize experimentally. In contrast, traditional approach to the analysis of boundary layers utilizes spatially localized fluctuation sources and evaluates the streamwise growth of fluctuations as they convect downstream (Herbert Reference Herbert1997). However, in the presence of flow separation a parabolized approximation of the NS equations cannot be made. To evaluate amplification in different spatial regions, we restrict inputs and outputs to belong to a plane but still account for the global nature of the separated flow through the resolvent operator ![]() $(\mathrm {i}\omega \mathcal {I} - \mathcal {A}_{\beta })^{-1}$. As illustrated in figure 5(a), this is accomplished via a proper selection of the operators
$(\mathrm {i}\omega \mathcal {I} - \mathcal {A}_{\beta })^{-1}$. As illustrated in figure 5(a), this is accomplished via a proper selection of the operators ![]() $\mathcal {B}$ and
$\mathcal {B}$ and ![]() $\mathcal {C}$ in (3.8) by fixing the input location before flow separation, at
$\mathcal {C}$ in (3.8) by fixing the input location before flow separation, at ![]() $x_{in} = 25$, and by evaluating the output at different locations downstream of the separation,
$x_{in} = 25$, and by evaluating the output at different locations downstream of the separation, ![]() $x_{{out}}$. In this set-up,
$x_{{out}}$. In this set-up, ![]() $G_{x_{{out}}}$ quantifies the largest amplification at
$G_{x_{{out}}}$ quantifies the largest amplification at ![]() $x_{{out}}$ of disturbances that are introduced at
$x_{{out}}$ of disturbances that are introduced at ![]() $x_{in} = 25$.
$x_{in} = 25$.

Figure 5. Spatial input–output analysis: (a) input is introduced at a streamwise location ![]() $x_{in} = 25$ before separation and output is evaluated at
$x_{in} = 25$ before separation and output is evaluated at ![]() $x_{{out}}$; (b) dependence of the input–output gain
$x_{{out}}$; (b) dependence of the input–output gain ![]() $G_{x_{{out}}}$ on the streamwise location
$G_{x_{{out}}}$ on the streamwise location ![]() $x_{{out}}$ for streaks and oblique waves. Unsteady oblique waves with
$x_{{out}}$ for streaks and oblique waves. Unsteady oblique waves with ![]() $(\omega =0.4,\lambda _{z}=3)$ are strongly amplified throughout the separation zone.
$(\omega =0.4,\lambda _{z}=3)$ are strongly amplified throughout the separation zone.
Figure 5(b) shows the dependence of ![]() $G_{x_{{out}}}$ on
$G_{x_{{out}}}$ on ![]() $x_{{out}}$ for upstream disturbances with
$x_{{out}}$ for upstream disturbances with ![]() $(\omega =0,\lambda _{z}=1.5)$ and
$(\omega =0,\lambda _{z}=1.5)$ and ![]() $(\omega =0.4,\lambda _{z}=3)$. The gain associated with the steady fluctuations begins to grow in the latter half of the recirculation zone, especially near the reattachment location. In contrast, unsteady perturbations with
$(\omega =0.4,\lambda _{z}=3)$. The gain associated with the steady fluctuations begins to grow in the latter half of the recirculation zone, especially near the reattachment location. In contrast, unsteady perturbations with ![]() $\omega = 0.4$ experience significant amplification throughout the separation zone. This observation suggests that the separation zone plays a critical role in the amplification of unsteady fluctuations.
$\omega = 0.4$ experience significant amplification throughout the separation zone. This observation suggests that the separation zone plays a critical role in the amplification of unsteady fluctuations.
3.4. Amplification of oblique waves: physical mechanism
We now analyse physical mechanisms responsible for amplification of flow fluctuations within the separation zone in the presence of upstream unsteady disturbances. In particular, we examine the global response of the linearized equations to the input with (![]() $\omega =0.4,\lambda _{z}=3.0$) introduced prior to separation (i.e. at
$\omega =0.4,\lambda _{z}=3.0$) introduced prior to separation (i.e. at ![]() $x_{in}=25$) that triggers the largest amplification in the entire domain
$x_{in}=25$) that triggers the largest amplification in the entire domain ![]() $\varOmega$. The spatial structure of flow fluctuations is studied in the
$\varOmega$. The spatial structure of flow fluctuations is studied in the ![]() $(s,n,z)$ coordinate system which is locally aligned with the streamlines of the laminar 2-D base flow
$(s,n,z)$ coordinate system which is locally aligned with the streamlines of the laminar 2-D base flow ![]() $\bar {{\boldsymbol {\varPsi }}}$; see figure 3 for an illustration. In this frame of reference,
$\bar {{\boldsymbol {\varPsi }}}$; see figure 3 for an illustration. In this frame of reference, ![]() $\bar {\boldsymbol {u}} = (\bar {u}_s,0,0)$ with
$\bar {\boldsymbol {u}} = (\bar {u}_s,0,0)$ with ![]() $\bar {u}_{s} \geq 0$, and, as discussed in Finnigan (Reference Finnigan1983), Patel & Sotiropoulos (Reference Patel and Sotiropoulos1997), Dwivedi et al. (Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), this coordinate system is convenient for the analysis of separated boundary layers especially within the separation zone.
$\bar {u}_{s} \geq 0$, and, as discussed in Finnigan (Reference Finnigan1983), Patel & Sotiropoulos (Reference Patel and Sotiropoulos1997), Dwivedi et al. (Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), this coordinate system is convenient for the analysis of separated boundary layers especially within the separation zone.
The streamwise specific kinetic energy ![]() $\mathcal {E}_{s} \mathrel {\mathop :}= u_s^{\prime } u_s^{\prime }$ obeys the transport equation,
$\mathcal {E}_{s} \mathrel {\mathop :}= u_s^{\prime } u_s^{\prime }$ obeys the transport equation,
where ![]() $\mathcal {P}$,
$\mathcal {P}$, ![]() $\mathcal {S}$,
$\mathcal {S}$, ![]() $\mathcal {V}$ and
$\mathcal {V}$ and ![]() $\mathcal {K}$ are the production, source, viscous and curvature terms (see Appendix C), and
$\mathcal {K}$ are the production, source, viscous and curvature terms (see Appendix C), and ![]() $\mathcal {F}$ is the work done by external disturbances (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019, appendix C). The production term
$\mathcal {F}$ is the work done by external disturbances (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019, appendix C). The production term ![]() $\mathcal {P}$ quantifies interactions of fluctuation stresses with the base flow gradients, the source term
$\mathcal {P}$ quantifies interactions of fluctuation stresses with the base flow gradients, the source term ![]() $\mathcal {S}$ corresponds to the perturbation component of the inviscid material derivative, the viscous term
$\mathcal {S}$ corresponds to the perturbation component of the inviscid material derivative, the viscous term ![]() $\mathcal {V}$ determines dissipation of kinetic energy by viscous stresses and
$\mathcal {V}$ determines dissipation of kinetic energy by viscous stresses and ![]() $\mathcal {K}$ accounts for the curvature that arises from a coordinate transformation. Our computations indicate that while the dissipative viscous term
$\mathcal {K}$ accounts for the curvature that arises from a coordinate transformation. Our computations indicate that while the dissipative viscous term ![]() $\mathcal {V}$ is negative throughout the domain, the production term
$\mathcal {V}$ is negative throughout the domain, the production term ![]() $\mathcal {P}$ is sign indefinite,
$\mathcal {P}$ is sign indefinite, ![]() $\mathcal {S}$ and
$\mathcal {S}$ and ![]() $\mathcal {K}$ are negligible, and
$\mathcal {K}$ are negligible, and ![]() $\mathcal {F}$ is zero downstream of the forcing plane.
$\mathcal {F}$ is zero downstream of the forcing plane.
Insight into physical mechanisms can be gained by the analysis of dominant production terms in (3.17) associated with the global linearized response to upstream oblique disturbances. Averaging over the time period ![]() $T = {2{\rm \pi} }/{\omega }$ and the spanwise wavelength
$T = {2{\rm \pi} }/{\omega }$ and the spanwise wavelength ![]() $\lambda _{z} = 2 {\rm \pi}/ \beta$,
$\lambda _{z} = 2 {\rm \pi}/ \beta$, ![]() $\langle \,{\cdot }\,\rangle \mathrel {\mathop :}= ( T \lambda _{z} )^{-1}\int ^T_{0} \int ^{\lambda _{z}}_{0} (\,{\cdot }\,) \, \mathrm {d} z \,\mathrm {d} t$, and neglecting the terms that do not contribute significantly to the production of the averaged streamwise specific kinetic energy
$\langle \,{\cdot }\,\rangle \mathrel {\mathop :}= ( T \lambda _{z} )^{-1}\int ^T_{0} \int ^{\lambda _{z}}_{0} (\,{\cdot }\,) \, \mathrm {d} z \,\mathrm {d} t$, and neglecting the terms that do not contribute significantly to the production of the averaged streamwise specific kinetic energy ![]() $E_{s} \mathrel {\mathop :}= \langle \mathcal {E}_s \rangle$ yields the following approximation to the transport equation (3.17):
$E_{s} \mathrel {\mathop :}= \langle \mathcal {E}_s \rangle$ yields the following approximation to the transport equation (3.17):
Here ![]() ${R}_{sn} \mathrel {\mathop :}= \langle {u_s^{\prime } u_n^{\prime }}\rangle $ denotes the averaged shear stress of the streamwise velocity fluctuations. The second term on the left-hand side represents the production of fluctuations’ energy that arises from the streamwise gradient of the base flow
${R}_{sn} \mathrel {\mathop :}= \langle {u_s^{\prime } u_n^{\prime }}\rangle $ denotes the averaged shear stress of the streamwise velocity fluctuations. The second term on the left-hand side represents the production of fluctuations’ energy that arises from the streamwise gradient of the base flow ![]() $\partial _{s}\bar {u}_{s}$, and the term on the right-hand side determines the production term that originates from interactions of the base flow shear
$\partial _{s}\bar {u}_{s}$, and the term on the right-hand side determines the production term that originates from interactions of the base flow shear ![]() $\partial _n \bar {u}_{s}$ with the fluctuation shear stress
$\partial _n \bar {u}_{s}$ with the fluctuation shear stress ![]() ${R}_{sn}$.
${R}_{sn}$.
To understand the mechanism that facilitate the growth of ![]() $E_{s}$, we now investigate the streamwise transport of
$E_{s}$, we now investigate the streamwise transport of ![]() ${R}_{sn}$. In contrast to the transport equation for
${R}_{sn}$. In contrast to the transport equation for ![]() $E_{s}$, both the production
$E_{s}$, both the production ![]() $\mathcal {P}$ and curvature
$\mathcal {P}$ and curvature ![]() $\mathcal {K}$ terms contribute significantly to the streamwise transport of
$\mathcal {K}$ terms contribute significantly to the streamwise transport of ![]() ${R}_{sn}$ for fluctuations with
${R}_{sn}$ for fluctuations with ![]() $\omega =0.4$ and
$\omega =0.4$ and ![]() $\lambda _{z}=3.0$. As demonstrated in Appendix D, omitting negligible terms leads to the following approximate transport equation for
$\lambda _{z}=3.0$. As demonstrated in Appendix D, omitting negligible terms leads to the following approximate transport equation for ![]() ${R}_{sn}$:
${R}_{sn}$:
Here ![]() $K_{c}$ and
$K_{c}$ and ![]() $K_{s}$ denote contributions that arise from the curvature normal to the streamlines and from deceleration along the streamline direction, respectively,
$K_{s}$ denote contributions that arise from the curvature normal to the streamlines and from deceleration along the streamline direction, respectively,
In the ![]() $(s,n,z)$ coordinate system,
$(s,n,z)$ coordinate system, ![]() $\bar {\varOmega } = \partial _{x}\bar {v} - \partial _{y}\bar {u}$ denotes the spanwise vorticity of the base flow in Cartesian coordinates (Finnigan Reference Finnigan1983) and using the definition of
$\bar {\varOmega } = \partial _{x}\bar {v} - \partial _{y}\bar {u}$ denotes the spanwise vorticity of the base flow in Cartesian coordinates (Finnigan Reference Finnigan1983) and using the definition of ![]() $K_{s}$, (3.19a) simplifies to
$K_{s}$, (3.19a) simplifies to
In summary, (3.18) and (3.19c) determine a coupled system of linear equations that governs the streamwise transport of ![]() ${E_{s}}$ and
${E_{s}}$ and ![]() ${R}_{s n}$ in the separation zone for oblique fluctuations with (
${R}_{s n}$ in the separation zone for oblique fluctuations with (![]() $\omega =0.4,\lambda _{z}=3.0$),
$\omega =0.4,\lambda _{z}=3.0$),
Oblique waves experience the largest amplification in the separated shear layer above the recirculation bubble, i.e. in the region where the presence of flow separation leads to concave flow curvature ![]() $K_c<0$. Figure 6(a) shows this negative curvature along the separation streamline and figure 6(b) illustrates the physical mechanism which is absent in the attached boundary layers because of negligibly small positive streamwise curvature.
$K_c<0$. Figure 6(a) shows this negative curvature along the separation streamline and figure 6(b) illustrates the physical mechanism which is absent in the attached boundary layers because of negligibly small positive streamwise curvature.

Figure 6. (a) Curvature (![]() $-K_{c}$) of the laminar base flow along the separation streamline; (b) illustration of a physical mechanism that facilitates growth of the averaged streamwise specific kinetic energy
$-K_{c}$) of the laminar base flow along the separation streamline; (b) illustration of a physical mechanism that facilitates growth of the averaged streamwise specific kinetic energy ![]() $E_{s}$ of oblique fluctuations in the separated shear layer.
$E_{s}$ of oblique fluctuations in the separated shear layer.
Concave base flow curvature (i.e. ![]() $K_{c} < 0$) in the shear layer provides the destabilizing effect in system (3.20) that can be understood by simplifying (3.20) for oblique waves. In figure 7(a) we compare
$K_{c} < 0$) in the shear layer provides the destabilizing effect in system (3.20) that can be understood by simplifying (3.20) for oblique waves. In figure 7(a) we compare ![]() $\bar {u}_{s} \partial _s E_{s} \mathrel {\mathop :}= \bar {u}_{s} \partial E_{s} / \partial s$ with the dominant production term in (3.18) to illustrate that
$\bar {u}_{s} \partial _s E_{s} \mathrel {\mathop :}= \bar {u}_{s} \partial E_{s} / \partial s$ with the dominant production term in (3.18) to illustrate that ![]() $( \partial _n \bar {u}_{s} ){R}_{sn}$ dictates the streamwise growth of
$( \partial _n \bar {u}_{s} ){R}_{sn}$ dictates the streamwise growth of ![]() $E_{s}$. Furthermore, since the base shear
$E_{s}$. Furthermore, since the base shear ![]() $\partial _n \bar {u}_{s}$ remains almost constant throughout the shear layer (cf. figure 7b), its streamwise derivative can be neglected, thereby leading to
$\partial _n \bar {u}_{s}$ remains almost constant throughout the shear layer (cf. figure 7b), its streamwise derivative can be neglected, thereby leading to
This second-order differential equation for ![]() $E_s$ is obtained by taking the derivative of the equation for
$E_s$ is obtained by taking the derivative of the equation for ![]() $E_s$ in (3.20), keeping the dominant terms and substituting the equation for
$E_s$ in (3.20), keeping the dominant terms and substituting the equation for ![]() $R_{sn}$ from (3.20) into the resulting expression. Figure 8(a) shows the streamwise evolution of
$R_{sn}$ from (3.20) into the resulting expression. Figure 8(a) shows the streamwise evolution of ![]() $E_s$ and figure 8(b) compares the coefficients in (3.21). Since the effect of
$E_s$ and figure 8(b) compares the coefficients in (3.21). Since the effect of ![]() $\partial _{s} \bar {u}_{s}$ is negligible, (3.21) can further be simplified to obtain
$\partial _{s} \bar {u}_{s}$ is negligible, (3.21) can further be simplified to obtain

Figure 7. Streamwise variation of (a) ![]() $\bar {u}_s \partial _{s} E_{s}$ along with the dominant production term in (3.18); (b) average fluctuation shear stress
$\bar {u}_s \partial _{s} E_{s}$ along with the dominant production term in (3.18); (b) average fluctuation shear stress ![]() ${R}_{sn}$ and base flow shear
${R}_{sn}$ and base flow shear ![]() $\partial _{n} \bar {u}_{s}$.
$\partial _{n} \bar {u}_{s}$.

Figure 8. (a) Streamwise evolution of the wall-normal integral of ![]() $E_{s} \mathrel {\mathop :}= \langle u^\prime _s u^\prime _s \rangle$ for the primary output resolvent mode of oblique fluctuations with (
$E_{s} \mathrel {\mathop :}= \langle u^\prime _s u^\prime _s \rangle$ for the primary output resolvent mode of oblique fluctuations with (![]() $\omega =0.4,\lambda _{z}=3.0$) along with contours of
$\omega =0.4,\lambda _{z}=3.0$) along with contours of ![]() $E_{s}$ in the separated shear layer near reattachment (inset); (b) the coefficients in (3.21) along the separation shear layer.
$E_{s}$ in the separated shear layer near reattachment (inset); (b) the coefficients in (3.21) along the separation shear layer.
As shown in figure 8(b), the concave base flow curvature (i.e. ![]() $K_c < 0$) provides the destabilizing influence throughout the separated shear layer and a simple mechanical analogy can be used to explain amplification of oblique waves. In the regions where
$K_c < 0$) provides the destabilizing influence throughout the separated shear layer and a simple mechanical analogy can be used to explain amplification of oblique waves. In the regions where ![]() $K_c < 0$ the ‘spring constant’
$K_c < 0$ the ‘spring constant’ ![]() $4 K_c ( \partial _n \bar {u}_s)$ in (3.22) is negative and this system behaves as an inverted pendulum, which enables the spatial growth of
$4 K_c ( \partial _n \bar {u}_s)$ in (3.22) is negative and this system behaves as an inverted pendulum, which enables the spatial growth of ![]() $E_s$.
$E_s$.
In summary, we have utilized the resolvent analysis to identify the spatial structure of oblique fluctuations that amplify rapidly in the separation zone. Furthermore, by conducting transport analysis of the most energetic fluctuations, we have demonstrated that the resulting amplification arises from concave curvature of the laminar 2-D base flow.
4. Nonlinear interactions of oblique waves
In § 3 we used resolvent analysis to identify oblique waves as the most energetic responses of the linearized flow equations in the presence of unsteady disturbances. Recent numerical simulations (Lugrin et al. Reference Lugrin, Beneddine, Leclercq, Garnier and Bur2021) show that, even in the presence of unsteady disturbances, the dominant response near the reattachment appears in the form of streamwise streaks. To investigate the origin of steady streaks in the presence of unsteady external disturbances, we utilize a weakly nonlinear formulation based on a perturbation expansion in the amplitude of the oblique disturbances. While previous numerical studies of transition induced by oblique waves in low-speed channel (Schmid & Henningson Reference Schmid and Henningson1992) and boundary layer (Chang & Malik Reference Chang and Malik1994; Berlin & Henningson Reference Berlin and Henningson1999; Mayer et al. Reference Mayer, Von Terzi and Fasel2011) flows show that nonlinear interactions of oblique waves generate streaks, we focus on the origin and spatial growth of these streaks in separated high-speed compressible boundary layer flows.
4.1. Streaks generated by oblique waves: a weakly nonlinear analysis
In the presence of a small external disturbance,
a weakly nonlinear analysis of § 3.1 can be utilized to represent the flow state components in compressible NS equations (3.3) as
 \begin{equation} \left. \begin{aligned} {{O} (1):} & \quad \bar{{\boldsymbol{\varPsi}}} ({\boldsymbol{x}}, t) = \bar{{\boldsymbol{\varPsi}}} (x,y),\\ {{O} (\epsilon):} & \quad {\boldsymbol{\psi}}^{(1)}({\boldsymbol{x}}, t) = \left( \hat{{\boldsymbol{\psi}}}^{(1)}_{+}(x,y)\mathrm{e}^{\mathrm{i} \omega t} + \hat{{\boldsymbol{\psi}}}^{(1)}_{-}(x,y)\mathrm{e}^{-\mathrm{i} \omega t} \right) \mathrm{e}^{\mathrm{i} \beta z},\\ {{O} (\epsilon^2):} & \quad {\boldsymbol{\psi}}^{(2)}({\boldsymbol{x}}, t) = \left( \hat{{\boldsymbol{\psi}}}^{(2)}_{0} (x,y) + \hat{{\boldsymbol{\psi}}}^{(2)}_{+} (x,y) \mathrm{e}^{2 \mathrm{i} \omega t} + \hat{{\boldsymbol{\psi}}}^{(2)}_{-} (x,y) \mathrm{e}^{{-}2 \mathrm{i} \omega t} \right) \mathrm{e}^{2 \mathrm{i} \beta z}. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} {{O} (1):} & \quad \bar{{\boldsymbol{\varPsi}}} ({\boldsymbol{x}}, t) = \bar{{\boldsymbol{\varPsi}}} (x,y),\\ {{O} (\epsilon):} & \quad {\boldsymbol{\psi}}^{(1)}({\boldsymbol{x}}, t) = \left( \hat{{\boldsymbol{\psi}}}^{(1)}_{+}(x,y)\mathrm{e}^{\mathrm{i} \omega t} + \hat{{\boldsymbol{\psi}}}^{(1)}_{-}(x,y)\mathrm{e}^{-\mathrm{i} \omega t} \right) \mathrm{e}^{\mathrm{i} \beta z},\\ {{O} (\epsilon^2):} & \quad {\boldsymbol{\psi}}^{(2)}({\boldsymbol{x}}, t) = \left( \hat{{\boldsymbol{\psi}}}^{(2)}_{0} (x,y) + \hat{{\boldsymbol{\psi}}}^{(2)}_{+} (x,y) \mathrm{e}^{2 \mathrm{i} \omega t} + \hat{{\boldsymbol{\psi}}}^{(2)}_{-} (x,y) \mathrm{e}^{{-}2 \mathrm{i} \omega t} \right) \mathrm{e}^{2 \mathrm{i} \beta z}. \end{aligned} \right\} \end{equation}
Here, ![]() $\bar {{\boldsymbol {\varPsi }}} (x,y)$ is the 2-D laminar base flow,
$\bar {{\boldsymbol {\varPsi }}} (x,y)$ is the 2-D laminar base flow, ![]() $\hat {\boldsymbol {d}}^{(1)}_{\pm }$ and
$\hat {\boldsymbol {d}}^{(1)}_{\pm }$ and ![]() $\hat {{\boldsymbol {\psi }}}^{(1)}_{\pm }$ are the principal oblique input and state modes resulting from the linearized analysis of § 3, whereas
$\hat {{\boldsymbol {\psi }}}^{(1)}_{\pm }$ are the principal oblique input and state modes resulting from the linearized analysis of § 3, whereas ![]() $\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$ and
$\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$ and ![]() $\hat {{\boldsymbol {\psi }}}^{(2)}_{\pm }$ are the steady and harmonic components of the state at
$\hat {{\boldsymbol {\psi }}}^{(2)}_{\pm }$ are the steady and harmonic components of the state at ![]() ${O}(\epsilon ^2)$. At
${O}(\epsilon ^2)$. At ![]() ${O}(\epsilon ^2)$, the fluctuation's dynamics is governed by (3.5b), where the steady component
${O}(\epsilon ^2)$, the fluctuation's dynamics is governed by (3.5b), where the steady component ![]() $\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$ satisfies
$\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$ satisfies
Here, ![]() $\mathcal {A}_{2 \beta }$ is the Fourier symbol of the dynamical generator in the linearized state-space model (3.8) and
$\mathcal {A}_{2 \beta }$ is the Fourier symbol of the dynamical generator in the linearized state-space model (3.8) and ![]() $\hat {\boldsymbol {d}}^{(2)}_0 \mathrel {\mathop :}= \mathcal {N}^{(2)}_0 ( \hat {{\boldsymbol {\psi }}}^{(1)}_{\pm } )$ is the forcing term that arises from quadratic interactions of
$\hat {\boldsymbol {d}}^{(2)}_0 \mathrel {\mathop :}= \mathcal {N}^{(2)}_0 ( \hat {{\boldsymbol {\psi }}}^{(1)}_{\pm } )$ is the forcing term that arises from quadratic interactions of ![]() ${O} (\epsilon )$ oblique waves with the spanwise wavenumber
${O} (\epsilon )$ oblique waves with the spanwise wavenumber ![]() $\beta$; see Appendix A for details. Thus, the resolvent operator associated with (3.8) evaluated at (
$\beta$; see Appendix A for details. Thus, the resolvent operator associated with (3.8) evaluated at (![]() $\omega = 0$,
$\omega = 0$, ![]() $2 \beta$) maps the nonlinear modulation
$2 \beta$) maps the nonlinear modulation ![]() $\hat {\boldsymbol {d}}^{(2)}_0$ of
$\hat {\boldsymbol {d}}^{(2)}_0$ of ![]() ${O}(\epsilon )$ oblique waves to
${O}(\epsilon )$ oblique waves to ![]() ${O}(\epsilon ^{2})$ steady streamwise streaks,
${O}(\epsilon ^{2})$ steady streamwise streaks,
To investigate the emergence of streaks from unsteady disturbances, we introduce forcing inputs with (![]() $\omega =\pm 0.4, \lambda _{z}=3$) and examine a weakly nonlinear evolution of the resulting oblique waves. These forcing inputs are introduced at the upstream plane
$\omega =\pm 0.4, \lambda _{z}=3$) and examine a weakly nonlinear evolution of the resulting oblique waves. These forcing inputs are introduced at the upstream plane ![]() $x_{{in}} = 25$ and their spatial structure is identified using the resolvent analysis of § 3 to generate the most energetic response at the reattachment (i.e. at
$x_{{in}} = 25$ and their spatial structure is identified using the resolvent analysis of § 3 to generate the most energetic response at the reattachment (i.e. at ![]() $x_{out}=60$).
$x_{out}=60$).
Figure 9(a) illustrates the set-up in which disturbances corresponding to a pair of oblique input modes ![]() $\hat {\boldsymbol {d}}^{(1)}_{\pm }$ with (
$\hat {\boldsymbol {d}}^{(1)}_{\pm }$ with (![]() $\omega =\pm 0.4,\ \lambda _{z}=3$) are introduced at
$\omega =\pm 0.4,\ \lambda _{z}=3$) are introduced at ![]() $x_{in}= 25$. The resulting response of the linearized dynamics consists of oblique waves with opposite phase velocities, leading to a checkerboard wave pattern in the spanwise direction. Figure 9(b) shows the streamwise velocity component of the steady response
$x_{in}= 25$. The resulting response of the linearized dynamics consists of oblique waves with opposite phase velocities, leading to a checkerboard wave pattern in the spanwise direction. Figure 9(b) shows the streamwise velocity component of the steady response ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0} (x,y)$ at
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0} (x,y)$ at ![]() ${O} (\epsilon ^2)$ that arises from weakly nonlinear interactions of
${O} (\epsilon ^2)$ that arises from weakly nonlinear interactions of ![]() ${O} (\epsilon )$ oblique waves. The steady response is given by streamwise streaks with half the spanwise wavelength
${O} (\epsilon )$ oblique waves. The steady response is given by streamwise streaks with half the spanwise wavelength ![]() $\lambda ^{\textit {streaks}}_{z} = \lambda ^{\textit {oblique}}_{z}/2 = 1.5$ of the oblique input.
$\lambda ^{\textit {streaks}}_{z} = \lambda ^{\textit {oblique}}_{z}/2 = 1.5$ of the oblique input.

Figure 9. (a) Set-up for weakly nonlinear analysis: a pair of dominant input modes with (![]() $\omega =\pm 0.4, \lambda _{z}=3$) resulting from resolvent analysis is introduced at
$\omega =\pm 0.4, \lambda _{z}=3$) resulting from resolvent analysis is introduced at ![]() $x_{{in}} = 25$ and the corresponding streamwise velocity fluctuations arise as the output of the linearized dynamics. Panel (b) shows that
$x_{{in}} = 25$ and the corresponding streamwise velocity fluctuations arise as the output of the linearized dynamics. Panel (b) shows that ![]() ${O} (\epsilon ^2)$ steady streamwise streaks with
${O} (\epsilon ^2)$ steady streamwise streaks with ![]() $\lambda _z = 1.5$ are triggered by weakly nonlinear interactions of
$\lambda _z = 1.5$ are triggered by weakly nonlinear interactions of ![]() ${O} (\epsilon )$ oblique waves with
${O} (\epsilon )$ oblique waves with ![]() $\lambda _{z}=3$.
$\lambda _{z}=3$.
A weakly nonlinear analysis allows us to demonstrate that steady streaks at ![]() ${O}(\epsilon ^2)$ arise from quadratic interactions of
${O}(\epsilon ^2)$ arise from quadratic interactions of ![]() ${O}(\epsilon )$ oblique waves. Figure 10(a) utilizes a wall-aligned (
${O}(\epsilon )$ oblique waves. Figure 10(a) utilizes a wall-aligned (![]() $\xi,\eta$) coordinate system to illustrate the forcing term
$\xi,\eta$) coordinate system to illustrate the forcing term ![]() $\hat {\boldsymbol {d}}^{(2)}_0 \mathrel {\mathop :}= \mathcal {N}^{(2)}_0 ( \hat {{\boldsymbol {\psi }}}^{(1)}_{\pm } )$ in (4.3), where
$\hat {\boldsymbol {d}}^{(2)}_0 \mathrel {\mathop :}= \mathcal {N}^{(2)}_0 ( \hat {{\boldsymbol {\psi }}}^{(1)}_{\pm } )$ in (4.3), where ![]() $\xi$ and
$\xi$ and ![]() $\eta$ denote the directions parallel and normal to the wall, respectively. Large amplification of oblique waves that result from linearized analysis in the reattachment region triggers strongest forcing
$\eta$ denote the directions parallel and normal to the wall, respectively. Large amplification of oblique waves that result from linearized analysis in the reattachment region triggers strongest forcing ![]() $\hat {\boldsymbol {d}}^{(2)}_{0}$ in that region. Figure 10(b) shows the wall-normal profiles of the forcing term to the mass, momentum and temperature equations in (4.3) before reattachment at
$\hat {\boldsymbol {d}}^{(2)}_{0}$ in that region. Figure 10(b) shows the wall-normal profiles of the forcing term to the mass, momentum and temperature equations in (4.3) before reattachment at ![]() $x = 58$. We observe the strongest contribution of the forcing to the wall-normal and spanwise components of the momentum equations, thereby demonstrating its vortical nature. Figure 10(c) illustrates the spatial structure of the forcing near reattachment in the (
$x = 58$. We observe the strongest contribution of the forcing to the wall-normal and spanwise components of the momentum equations, thereby demonstrating its vortical nature. Figure 10(c) illustrates the spatial structure of the forcing near reattachment in the (![]() $z,\eta$) plane. The forcing term
$z,\eta$) plane. The forcing term ![]() $\hat {\boldsymbol {d}}^{(2)}_{0}$ which forms counter-rotating vortices in the separated shear layer is
$\hat {\boldsymbol {d}}^{(2)}_{0}$ which forms counter-rotating vortices in the separated shear layer is ![]() $90^{\circ }$ out of phase relative to the induced streak response
$90^{\circ }$ out of phase relative to the induced streak response ![]() $u^\prime _s$. In contrast to the dominant vortical forcing resulting from the linearized analysis, the vortical source term that arises from weakly nonlinear interactions of oblique waves primarily lies downstream of the recirculation zone.
$u^\prime _s$. In contrast to the dominant vortical forcing resulting from the linearized analysis, the vortical source term that arises from weakly nonlinear interactions of oblique waves primarily lies downstream of the recirculation zone.

Figure 10. (a) Real part of the streamwise vorticity forcing component that arises from weakly nonlinear interactions of oblique waves ![]() $\hat {\boldsymbol {d}}^{(2)}_0$ in the (
$\hat {\boldsymbol {d}}^{(2)}_0$ in the (![]() $x,y$) plane along with the base flow streamlines. (b) Wall-normal profiles of the forcing terms to the streamwise vorticity, density, temperature and streamwise velocity equations that originate from
$x,y$) plane along with the base flow streamlines. (b) Wall-normal profiles of the forcing terms to the streamwise vorticity, density, temperature and streamwise velocity equations that originate from ![]() $\hat {\boldsymbol {d}}^{(2)}_0$ before reattachment, at
$\hat {\boldsymbol {d}}^{(2)}_0$ before reattachment, at ![]() $x = 58$. (c) Spatial structure of the forcing
$x = 58$. (c) Spatial structure of the forcing ![]() $\hat {\boldsymbol {d}}^{(2)}_0$ near reattachment in the (
$\hat {\boldsymbol {d}}^{(2)}_0$ near reattachment in the (![]() $z,\eta$) plane (colour plots) along with the resulting streak response
$z,\eta$) plane (colour plots) along with the resulting streak response ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_0$ (contour lines) at
$\hat {{\boldsymbol {\phi }}}^{(2)}_0$ (contour lines) at ![]() $x = 58$.
$x = 58$.
We utilize DNS to verify the predictions of weakly nonlinear analysis. In DNS the input oblique modes ![]() $\hat {\boldsymbol {d}}^{(1)}_{\pm }$ (with
$\hat {\boldsymbol {d}}^{(1)}_{\pm }$ (with ![]() $\omega =\pm 0.4$,
$\omega =\pm 0.4$, ![]() $\lambda _z = 3$ and reference amplitude
$\lambda _z = 3$ and reference amplitude ![]() $A_{0} = 1.0$) are introduced in the plane
$A_{0} = 1.0$) are introduced in the plane ![]() $x_{in} = 25$. Additional details about the grid resolution and numerical implementation in our DNS study are provided in § 5. Figure 11 shows the spatial evolution of steady streamwise velocity fluctuations
$x_{in} = 25$. Additional details about the grid resolution and numerical implementation in our DNS study are provided in § 5. Figure 11 shows the spatial evolution of steady streamwise velocity fluctuations ![]() $u^\prime _s$ along the base flow separation streamline that are triggered by unsteady oblique disturbances of different amplitudes. As shown in figure 11(a), steady streaks undergo similar spatial growth across the range of forcing amplitudes. Figure 11(b) illustrates that the magnitude of streamwise velocity fluctuations collapses when scaled with
$u^\prime _s$ along the base flow separation streamline that are triggered by unsteady oblique disturbances of different amplitudes. As shown in figure 11(a), steady streaks undergo similar spatial growth across the range of forcing amplitudes. Figure 11(b) illustrates that the magnitude of streamwise velocity fluctuations collapses when scaled with ![]() $A^2_0$. This demonstrates an excellent agreement between streak profiles resulting from DNS and a weakly nonlinear analysis (that leads to (4.3)). Deviations from predictions of the weakly nonlinear analysis are only observed for the largest amplitude considered and they are manifested by the saturation of streaks in the post-reattachment region.
$A^2_0$. This demonstrates an excellent agreement between streak profiles resulting from DNS and a weakly nonlinear analysis (that leads to (4.3)). Deviations from predictions of the weakly nonlinear analysis are only observed for the largest amplitude considered and they are manifested by the saturation of streaks in the post-reattachment region.

Figure 11. (a) Streamwise velocity fluctuations ![]() $u_s^{\prime }$ along the separation streamline associated with
$u_s^{\prime }$ along the separation streamline associated with ![]() ${O}(\epsilon ^{2})$ steady streaks at
${O}(\epsilon ^{2})$ steady streaks at ![]() $\lambda _z = 1.5$; DNS results for various amplitudes of oblique disturbances with (
$\lambda _z = 1.5$; DNS results for various amplitudes of oblique disturbances with (![]() $\omega =\pm 0.4, \lambda _{z}=3$) are shown. (b) Direct numerical simulation results normalized with the square of the amplitude
$\omega =\pm 0.4, \lambda _{z}=3$) are shown. (b) Direct numerical simulation results normalized with the square of the amplitude ![]() $A_{0}$ of oblique disturbances are compared with the results of weakly nonlinear analysis.
$A_{0}$ of oblique disturbances are compared with the results of weakly nonlinear analysis.
Collapse of spatial profiles that characterize the amplification of streaks irrespective of the amplitude of oblique disturbances, which differ by ![]() ${O}(10^4)$, shows that streaks generated via quadratic interactions of oblique waves undergo linear amplification in the separation zone. This demonstrates the predictive power of the weakly nonlinear analysis across the range of forcing amplitudes. In what follows, we utilize the input–output modes obtained from the resolvent analysis to characterize evolution of
${O}(10^4)$, shows that streaks generated via quadratic interactions of oblique waves undergo linear amplification in the separation zone. This demonstrates the predictive power of the weakly nonlinear analysis across the range of forcing amplitudes. In what follows, we utilize the input–output modes obtained from the resolvent analysis to characterize evolution of ![]() ${O} (\epsilon ^2)$ steady streamwise streaks and uncover corresponding amplification mechanisms.
${O} (\epsilon ^2)$ steady streamwise streaks and uncover corresponding amplification mechanisms.
4.2. Resolvent mode representation of  ${O}(\epsilon ^{2})$ streaks
${O}(\epsilon ^{2})$ streaks
As described in § 3.2, the left and right singular function of the frequency response operator provide orthonormal bases of input and output spaces that can be used to study responses of the double-wedge flow to external excitations. In particular, ![]() ${O} (\epsilon ^{2})$ steady streaks resulting from weakly nonlinear interactions of
${O} (\epsilon ^{2})$ steady streaks resulting from weakly nonlinear interactions of ![]() ${O} (\epsilon )$ unsteady oblique waves (cf. (4.4)) can be represented using SVD of the frequency response operator associated with the linearized system (3.8) at
${O} (\epsilon )$ unsteady oblique waves (cf. (4.4)) can be represented using SVD of the frequency response operator associated with the linearized system (3.8) at ![]() $\omega = 0$ and the spanwise wavenumber
$\omega = 0$ and the spanwise wavenumber ![]() $2 \beta$,
$2 \beta$,
Here, ![]() $a_{i} \mathrel {\mathop :}= \sigma _i \langle \boldsymbol {d}_{i}, \hat {\boldsymbol {d}}^{(2)}_{0} \rangle _E$, with
$a_{i} \mathrel {\mathop :}= \sigma _i \langle \boldsymbol {d}_{i}, \hat {\boldsymbol {d}}^{(2)}_{0} \rangle _E$, with ![]() $\hat {\boldsymbol {d}}^{(2)}_{0} \mathrel {\mathop :}= \mathcal {N}^{(2)}_{0} (\hat {{\boldsymbol {\psi }}}_{\pm }^{(1)})$, quantifies the contribution of the
$\hat {\boldsymbol {d}}^{(2)}_{0} \mathrel {\mathop :}= \mathcal {N}^{(2)}_{0} (\hat {{\boldsymbol {\psi }}}_{\pm }^{(1)})$, quantifies the contribution of the ![]() $i$th output mode
$i$th output mode ![]() ${\boldsymbol {\phi }}_{i}$ of
${\boldsymbol {\phi }}_{i}$ of ![]() $\mathcal {H}_{2 \beta } (0)$ to
$\mathcal {H}_{2 \beta } (0)$ to ![]() ${O} (\epsilon ^{2})$ steady streaks
${O} (\epsilon ^{2})$ steady streaks ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$,
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$, ![]() $\sigma _{i}$ is the
$\sigma _{i}$ is the ![]() $i$th singular value, (
$i$th singular value, (![]() $\boldsymbol {d}_{i},{\boldsymbol {\phi }} _{i}$) are the corresponding input–output modes of
$\boldsymbol {d}_{i},{\boldsymbol {\phi }} _{i}$) are the corresponding input–output modes of ![]() $\mathcal {H}_{2 \beta } (0)$ and, for
$\mathcal {H}_{2 \beta } (0)$ and, for ![]() $\lambda _z = 1.5$, the inner product
$\lambda _z = 1.5$, the inner product ![]() $\langle \,{\cdot }\, , \,{\cdot }\, \rangle _{E}$ is carried over the entire flow domain in (
$\langle \,{\cdot }\, , \,{\cdot }\, \rangle _{E}$ is carried over the entire flow domain in (![]() $x,y$).
$x,y$).
Figure 12(a) shows the ![]() $15$ largest singular values of the resolvent for the linearized system (3.8) with (
$15$ largest singular values of the resolvent for the linearized system (3.8) with (![]() $\omega = 0, \lambda _{z} = 1.5$). Even though the principal singular value
$\omega = 0, \lambda _{z} = 1.5$). Even though the principal singular value ![]() $\sigma _1$ is an order of magnitude larger than
$\sigma _1$ is an order of magnitude larger than ![]() $\sigma _2$, figure 12(b) demonstrates that the second output mode
$\sigma _2$, figure 12(b) demonstrates that the second output mode ![]() ${\boldsymbol {\phi }}_2$ contributes most to
${\boldsymbol {\phi }}_2$ contributes most to ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$. Figure 13(a) shows the wall-normal profiles of the streamwise velocity component
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$. Figure 13(a) shows the wall-normal profiles of the streamwise velocity component ![]() $u^{\prime }$ associated with
$u^{\prime }$ associated with ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ and the first two output modes (
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ and the first two output modes (![]() ${\boldsymbol {\phi }}_1,{\boldsymbol {\phi }}_2$) of the resolvent. We observe a striking similarity between
${\boldsymbol {\phi }}_1,{\boldsymbol {\phi }}_2$) of the resolvent. We observe a striking similarity between ![]() ${O} (\epsilon ^{2})$ steady streaks and
${O} (\epsilon ^{2})$ steady streaks and ![]() ${\boldsymbol {\phi }}_{2}$ in the post-reattachment region, at
${\boldsymbol {\phi }}_{2}$ in the post-reattachment region, at ![]() $x = 65$. Similarly, figure 13(b) compares the wall-normal shapes of the corresponding input modes
$x = 65$. Similarly, figure 13(b) compares the wall-normal shapes of the corresponding input modes ![]() $\boldsymbol {d}_1$ and
$\boldsymbol {d}_1$ and ![]() $\boldsymbol {d}_2$ with the forcing
$\boldsymbol {d}_2$ with the forcing ![]() $\hat {\boldsymbol {d}}^{(2)}_0$ that arises from quadratic interactions. The input modes are visualized in the reattaching shear layer, at
$\hat {\boldsymbol {d}}^{(2)}_0$ that arises from quadratic interactions. The input modes are visualized in the reattaching shear layer, at ![]() $x = 57$, and the streamwise vorticity component of
$x = 57$, and the streamwise vorticity component of ![]() $\boldsymbol {d}_2$ provides a good approximation to the vortical forcing that captures interactions of unsteady oblique fluctuations.
$\boldsymbol {d}_2$ provides a good approximation to the vortical forcing that captures interactions of unsteady oblique fluctuations.

Figure 12. (a) Singular values of the resolvent operator associated with the linearized dynamics around the 2-D laminar flow evaluated at ![]() $(\omega,\lambda _z) = (0,1.5)$. (b) Contribution of the
$(\omega,\lambda _z) = (0,1.5)$. (b) Contribution of the ![]() $i$th output mode
$i$th output mode ![]() ${\boldsymbol {\phi }}_{i}$ to the energy of
${\boldsymbol {\phi }}_{i}$ to the energy of ![]() ${O}(\epsilon ^{2})$ steady streaks
${O}(\epsilon ^{2})$ steady streaks ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ that are triggered by weakly nonlinear interactions of
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ that are triggered by weakly nonlinear interactions of ![]() ${O}(\epsilon )$ oblique waves.
${O}(\epsilon )$ oblique waves.

Figure 13. The wall-normal profiles of the real part of streamwise velocity fluctuations resulting from weakly nonlinear interactions of oblique waves and corresponding to (a) ![]() ${O}(\epsilon ^{2})$ steady streaks
${O}(\epsilon ^{2})$ steady streaks ![]() $\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ and the first two output resolvent modes after reattachment, at
$\hat {{\boldsymbol {\phi }}}^{(2)}_{0}$ and the first two output resolvent modes after reattachment, at ![]() $x=65$; (b) steady vortical forcing
$x=65$; (b) steady vortical forcing ![]() $\hat {\boldsymbol{d}}^{(2)}_{0}$ and the first two input resolvent modes in the reattaching shear layer, at
$\hat {\boldsymbol{d}}^{(2)}_{0}$ and the first two input resolvent modes in the reattaching shear layer, at ![]() $x=57$.
$x=57$.
As demonstrated above, near reattachment, ![]() ${O}(\epsilon ^{2})$ streaks are well approximated by the second output mode of the resolvent associated with the linearized equations at (
${O}(\epsilon ^{2})$ streaks are well approximated by the second output mode of the resolvent associated with the linearized equations at (![]() $\omega = 0, \lambda _z = 1.5$). To gain insight into the amplification mechanism that generates
$\omega = 0, \lambda _z = 1.5$). To gain insight into the amplification mechanism that generates ![]() ${O} (\epsilon ^{2})$ streaks, we examine the dominant terms in the energy transport equation for the output mode
${O} (\epsilon ^{2})$ streaks, we examine the dominant terms in the energy transport equation for the output mode ![]() ${\boldsymbol {\phi }}_{2}$. Similar to the analysis in § 3.4, we utilize the (
${\boldsymbol {\phi }}_{2}$. Similar to the analysis in § 3.4, we utilize the (![]() $s,n,z$) coordinate system which is locally aligned with the streamlines of the base flow
$s,n,z$) coordinate system which is locally aligned with the streamlines of the base flow ![]() $(\bar {u}_{s},0,0)$. The transport of the spanwise-averaged specific kinetic energy of streamwise velocity fluctuations
$(\bar {u}_{s},0,0)$. The transport of the spanwise-averaged specific kinetic energy of streamwise velocity fluctuations ![]() $E_{s} = \langle {u^\prime _{s} u^{\prime }_s} \rangle$ and fluctuation shear stress
$E_{s} = \langle {u^\prime _{s} u^{\prime }_s} \rangle$ and fluctuation shear stress ![]() ${R}_{sn} = \langle u^\prime _{s} u^{\prime }_n \rangle$ associated with the second output mode is approximately governed by (3.20) in § 3.4.
${R}_{sn} = \langle u^\prime _{s} u^{\prime }_n \rangle$ associated with the second output mode is approximately governed by (3.20) in § 3.4.
Figure 14(a) shows the streamwise evolution of the wall-normal integral of ![]() $E_{s}$ for the mode
$E_{s}$ for the mode ![]() ${\boldsymbol {\phi }}_{2}$ associated with
${\boldsymbol {\phi }}_{2}$ associated with ![]() ${O} (\epsilon ^{2})$ streaks with (
${O} (\epsilon ^{2})$ streaks with (![]() $\omega = 0,\lambda _z = 1.5$). In contrast to the oblique waves (cf. figure 8a), which experience monotonic amplification throughout the separation shear layer above the recirculation bubble, we observe a non-monotonic
$\omega = 0,\lambda _z = 1.5$). In contrast to the oblique waves (cf. figure 8a), which experience monotonic amplification throughout the separation shear layer above the recirculation bubble, we observe a non-monotonic ![]() $x$-dependence of
$x$-dependence of ![]() $E_s$ for the streaks within the bubble. To gain physical insight, we evaluate the terms of the coefficient matrix in (3.20) for steady streaks. Figure 14(b) shows that both streamwise deceleration (i.e.
$E_s$ for the streaks within the bubble. To gain physical insight, we evaluate the terms of the coefficient matrix in (3.20) for steady streaks. Figure 14(b) shows that both streamwise deceleration (i.e. ![]() $\partial _{s} \bar {u}_{s} < 0$) and shear
$\partial _{s} \bar {u}_{s} < 0$) and shear ![]() $\partial _{n} \bar {u}$ contribute to amplification of
$\partial _{n} \bar {u}$ contribute to amplification of ![]() ${O} (\epsilon ^{2})$ streaks in different regions of the separated laminar flow. Towards reattachment, the base flow curvature
${O} (\epsilon ^{2})$ streaks in different regions of the separated laminar flow. Towards reattachment, the base flow curvature ![]() $K_c$ is positive inside the recirculation bubble (cf. figure 14c) and the streamwise deceleration term (i.e.
$K_c$ is positive inside the recirculation bubble (cf. figure 14c) and the streamwise deceleration term (i.e. ![]() $\partial _{s} \bar {u}_{s} < 0$) is primarily responsible for the energy
$\partial _{s} \bar {u}_{s} < 0$) is primarily responsible for the energy ![]() $E_{s}$ amplification. In this region, the transport equation for
$E_{s}$ amplification. In this region, the transport equation for ![]() $E_{s}$ can be approximated by
$E_{s}$ can be approximated by
This is in concert with the analysis of the contribution of the first (i.e. most amplified) output mode ![]() ${\boldsymbol {\phi }}_{1}$ to the amplification of streaks in a compression ramp flow (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), which also revealed dominance of streamwise deceleration near reattachment. On the other hand, in the post-reattachment region the shear term
${\boldsymbol {\phi }}_{1}$ to the amplification of streaks in a compression ramp flow (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), which also revealed dominance of streamwise deceleration near reattachment. On the other hand, in the post-reattachment region the shear term ![]() $\partial _{n} \bar {u}_{s} < 0$ dominates and the coupled system of (3.20) for
$\partial _{n} \bar {u}_{s} < 0$ dominates and the coupled system of (3.20) for ![]() $E_s$ and
$E_s$ and ![]() $R_{sn}$ simplifies to the following second-order equation (3.22) for
$R_{sn}$ simplifies to the following second-order equation (3.22) for ![]() $E_s$:
$E_s$:
Thus, in the post-reattachment region the concave streamline curvature of the laminar 2-D base flow (i.e. ![]() $K_c < 0$) is primarily responsible for amplification of
$K_c < 0$) is primarily responsible for amplification of ![]() ${O} (\epsilon ^{2})$ streaks.
${O} (\epsilon ^{2})$ streaks.

Figure 14. (a) Streamwise evolution of the wall-normal integral of ![]() $E_{s} = \langle {u^\prime _{s} u^{\prime }_s} \rangle$ for the second output mode associated with streaks at (
$E_{s} = \langle {u^\prime _{s} u^{\prime }_s} \rangle$ for the second output mode associated with streaks at (![]() $\omega = 0, \lambda _z = 1.5$) along with contours of
$\omega = 0, \lambda _z = 1.5$) along with contours of ![]() $E_{s}$ near reattachment (inset); (b) streamwise variation of deceleration and shear components of the spanwise-averaged production term
$E_{s}$ near reattachment (inset); (b) streamwise variation of deceleration and shear components of the spanwise-averaged production term ![]() $\langle \mathcal {P} \rangle$ in the transport equation for
$\langle \mathcal {P} \rangle$ in the transport equation for ![]() $E_{s}$; and (c) base flow curvature
$E_{s}$; and (c) base flow curvature ![]() $K_{c}$ near reattachment.
$K_{c}$ near reattachment.
5. Direct numerical simulations of streak breakdown
Weakly nonlinear analysis demonstrates that small unsteady disturbances induce steady streaks in a hypersonic flow over a double wedge. These streaks result from quadratic interactions of oblique waves and they undergo rapid amplification near reattachment. Downstream of reattachment, the streaks grow large enough to modify the time-averaged 2-D flow and we utilize DNS to examine the breakdown of streaks. We also report instantaneous and statistical properties of the flow as it transitions to turbulence.
5.1. Numerical set-up
To study the onset of transition, we extend the computational domain in the streamwise direction downstream of reattachment. We place the inflow boundary at ![]() $x=20$ and, at this location, we interpolate the inflow profile that results from 2-D base flow computations. To avoid spurious numerical errors, we utilize a non-reflecting numerical sponge near the outflow. The wall is assumed to be adiabatic and periodic boundary conditions in the spanwise direction are applied.
$x=20$ and, at this location, we interpolate the inflow profile that results from 2-D base flow computations. To avoid spurious numerical errors, we utilize a non-reflecting numerical sponge near the outflow. The wall is assumed to be adiabatic and periodic boundary conditions in the spanwise direction are applied.
A computational domain of size ![]() $80 \times 13 \times 9$ in the streamwise, wall-normal and spanwise directions is discretized using
$80 \times 13 \times 9$ in the streamwise, wall-normal and spanwise directions is discretized using ![]() $900 \times 249 \times 384$ grid points (i.e.
$900 \times 249 \times 384$ grid points (i.e. ![]() $86$ million cells). The grid is constructed to ensure uniform spacing in the streamwise and spanwise directions and, in the normal direction, the mesh is stretched to ensure
$86$ million cells). The grid is constructed to ensure uniform spacing in the streamwise and spanwise directions and, in the normal direction, the mesh is stretched to ensure ![]() $y^{+} < 0.22$ at the wall. In Appendix E we provide a grid convergence study and compare the numerical resolution that we use with recent simulations of supersonic and hypersonic transitional and turbulent flows. Our simulations utilize low-dissipation sixth-order spatially accurate kinetic-energy-consistent (KEC) fluxes (Subbareddy & Candler Reference Subbareddy and Candler2009) for spatial discretization. The low-dissipation KEC fluxes were previously employed in high-fidelity simulations of transitional and turbulent hypersonic boundary layers (Subbareddy & Candler Reference Subbareddy and Candler2012; Subbareddy, Bartkowicz & Candler Reference Subbareddy, Bartkowicz and Candler2014). The time integration is carried out using the explicit third-order Runge–Kutta scheme with a Courant–Friedrichs–Lewy number of
$y^{+} < 0.22$ at the wall. In Appendix E we provide a grid convergence study and compare the numerical resolution that we use with recent simulations of supersonic and hypersonic transitional and turbulent flows. Our simulations utilize low-dissipation sixth-order spatially accurate kinetic-energy-consistent (KEC) fluxes (Subbareddy & Candler Reference Subbareddy and Candler2009) for spatial discretization. The low-dissipation KEC fluxes were previously employed in high-fidelity simulations of transitional and turbulent hypersonic boundary layers (Subbareddy & Candler Reference Subbareddy and Candler2012; Subbareddy, Bartkowicz & Candler Reference Subbareddy, Bartkowicz and Candler2014). The time integration is carried out using the explicit third-order Runge–Kutta scheme with a Courant–Friedrichs–Lewy number of ![]() $0.5$.
$0.5$.
5.2. Secondary instability and breakdown
To simulate the breakdown of streaks, we excite the laminar 2-D flow using the oblique input modes with (![]() $\omega = \pm 0.4, \lambda _z=3$). The disturbance amplitude is set to
$\omega = \pm 0.4, \lambda _z=3$). The disturbance amplitude is set to ![]() $A_{ob} = 2.50 \times 10^{2} {A}_{0}$ and is determined based on the results reported in figure 11. With this amplitude, fluctuations grow linearly in the recirculation region but saturate nonlinearly post-reattachment (i.e. beyond
$A_{ob} = 2.50 \times 10^{2} {A}_{0}$ and is determined based on the results reported in figure 11. With this amplitude, fluctuations grow linearly in the recirculation region but saturate nonlinearly post-reattachment (i.e. beyond ![]() $x=60$).
$x=60$).
In figure 15 we show the time evolution of streaks in the plane close to the wall, at ![]() $\eta = 0.25$, for three different values of
$\eta = 0.25$, for three different values of ![]() $x$. These plots demonstrate that, in the presence of unsteady oblique disturbances,
$x$. These plots demonstrate that, in the presence of unsteady oblique disturbances, ![]() ${O}(\epsilon ^{2})$ steady streaks undergo spanwise motion close to reattachment. The identified spanwise oscillations become stronger as we progress downstream and their period corresponds to the time period of oblique wave inputs. We note the presence of a ‘sinuous-subharmonic’ motion, where two adjacent low-speed streaks oscillate out of phase, and observe that the amplitude of spanwise oscillations almost doubles as we move from
${O}(\epsilon ^{2})$ steady streaks undergo spanwise motion close to reattachment. The identified spanwise oscillations become stronger as we progress downstream and their period corresponds to the time period of oblique wave inputs. We note the presence of a ‘sinuous-subharmonic’ motion, where two adjacent low-speed streaks oscillate out of phase, and observe that the amplitude of spanwise oscillations almost doubles as we move from ![]() $x=55$ to
$x=55$ to ![]() $x = 65$.
$x = 65$.

Figure 15. Streamwise streaks in the plane close to the wall, ![]() $\eta = 0.25$, at three different streamwise locations: (a) before reattachment, at
$\eta = 0.25$, at three different streamwise locations: (a) before reattachment, at ![]() $x = 55$; (b) at reattachment, at
$x = 55$; (b) at reattachment, at ![]() $x = 60$; and (c) after reattachment, at
$x = 60$; and (c) after reattachment, at ![]() $x=65$. The low-speed streaks are marked in blue (solid lines) and high-speed streaks are marked in red (dashed lines).
$x=65$. The low-speed streaks are marked in blue (solid lines) and high-speed streaks are marked in red (dashed lines).
In figure 16 we illustrate the effect of streak oscillations on the mean flow by visualizing the root mean square (r.m.s.) of temporal fluctuations in the streamwise velocity. At different streamwise locations, fluctuations are plotted against ![]() $\partial \bar {u}/\partial z$, which characterizes steady spanwise variations of the mean flow. Initially, unsteadiness is restricted to the oblique wave pair, which is located further away from the wall relative to the streaks. However, at
$\partial \bar {u}/\partial z$, which characterizes steady spanwise variations of the mean flow. Initially, unsteadiness is restricted to the oblique wave pair, which is located further away from the wall relative to the streaks. However, at ![]() $x=65$, unsteadiness is observed in the region of the largest spanwise shear because of the presence of streaks. This ‘locking-in’ of
$x=65$, unsteadiness is observed in the region of the largest spanwise shear because of the presence of streaks. This ‘locking-in’ of ![]() $u_{rms}$ with streak oscillations identifies late stages of the streak evolution just before smaller scales (associated with higher frequencies) set in.
$u_{rms}$ with streak oscillations identifies late stages of the streak evolution just before smaller scales (associated with higher frequencies) set in.

Figure 16. Colour plots of the spanwise gradient of time-averaged streamwise velocity ![]() ${\partial \bar {u}}/{\partial z}$ and contour lines of
${\partial \bar {u}}/{\partial z}$ and contour lines of ![]() $u^{\prime }_{rms}$ at the same streamwise locations as in figure 15.
$u^{\prime }_{rms}$ at the same streamwise locations as in figure 15.
The amplification of streaks and their unsteadiness induce rapid steepening of spanwise and wall-normal mean flow gradients, thereby leading to the emergence of inflection points in the mean (time- and spanwise-averaged) flow. Figure 17(a) shows the resulting inflectional mean flow profile and figure 17(b) shows the location of unsteady fluctuations with respect to the streaks. As we move from ![]() $x=65$ to
$x=65$ to ![]() $x=70$, we note the appearance of higher spanwise wavenumbers in the streaks as well as in the unsteady fluctuations. As discussed by Hall & Horseman (Reference Hall and Horseman1991) and Yu & Liu (Reference Yu and Liu1994), inflectional points in the mean velocity serve as an indicator of its susceptibility to the growth of broadband fluctuations. Amplification of high-frequency harmonics is also observed in the temporal spectra of the fluctuations. Therefore, at
$x=70$, we note the appearance of higher spanwise wavenumbers in the streaks as well as in the unsteady fluctuations. As discussed by Hall & Horseman (Reference Hall and Horseman1991) and Yu & Liu (Reference Yu and Liu1994), inflectional points in the mean velocity serve as an indicator of its susceptibility to the growth of broadband fluctuations. Amplification of high-frequency harmonics is also observed in the temporal spectra of the fluctuations. Therefore, at ![]() $x=70$, flow is well within fully nonlinear stages of transition. We also note the strong spatial correlation of unsteady fluctuations with the spanwise shear associated with the streaks, even at this nonlinear stage.
$x=70$, flow is well within fully nonlinear stages of transition. We also note the strong spatial correlation of unsteady fluctuations with the spanwise shear associated with the streaks, even at this nonlinear stage.

Figure 17. (a) Wall-normal profiles of laminar and mean streamwise velocity components at ![]() $x = 70$. (b) Colour plots of
$x = 70$. (b) Colour plots of ![]() $u^{\prime }_{rms}$ along with contour lines of time-averaged streamwise velocity.
$u^{\prime }_{rms}$ along with contour lines of time-averaged streamwise velocity.
In figure 18 we plot ![]() $Q$-isosurfaces of the instantaneous flow field. These visualize vortical structures that arise from the sinuous-subharmonic motion of the streaks, prior to breakdown of the flow. We note the appearance of staggered lambda vortices, similar to those identified in transition induced by oblique waves in incompressible boundary layers (Berlin et al. Reference Berlin, Wiegel and Henningson1999). These vortical structures are also sometimes referred to as
$Q$-isosurfaces of the instantaneous flow field. These visualize vortical structures that arise from the sinuous-subharmonic motion of the streaks, prior to breakdown of the flow. We note the appearance of staggered lambda vortices, similar to those identified in transition induced by oblique waves in incompressible boundary layers (Berlin et al. Reference Berlin, Wiegel and Henningson1999). These vortical structures are also sometimes referred to as ![]() $X$-vortices, for reasons illustrated in the (
$X$-vortices, for reasons illustrated in the (![]() $\eta,z$) slice array plot in figure 18. Initially, at
$\eta,z$) slice array plot in figure 18. Initially, at ![]() $x \approx 62$, we observe that the interaction with the oblique waves causes the roll-up of the low-speed streak as they come together due to sinuous-subharmonic motion. Further downstream, as the flow structures associated with the
$x \approx 62$, we observe that the interaction with the oblique waves causes the roll-up of the low-speed streak as they come together due to sinuous-subharmonic motion. Further downstream, as the flow structures associated with the ![]() $X$-vortices spread apart, we see that wall-normal jets of low-speed flow form mushroom structures. As these low-speed regions oscillate further, they interact to generate fluctuations with higher spanwise wavenumbers. Finally, at
$X$-vortices spread apart, we see that wall-normal jets of low-speed flow form mushroom structures. As these low-speed regions oscillate further, they interact to generate fluctuations with higher spanwise wavenumbers. Finally, at ![]() $x\approx 70$, the shear introduced by the upward jets of low-speed streaks becomes significant enough to cause a local Kelvin–Helmholtz instability that induces streamwise rollers (Reddy et al. Reference Reddy, Schmid, Baggett and Henningson1998). At this stage, the laminar boundary layer flow has started to break down to turbulence.
$x\approx 70$, the shear introduced by the upward jets of low-speed streaks becomes significant enough to cause a local Kelvin–Helmholtz instability that induces streamwise rollers (Reddy et al. Reference Reddy, Schmid, Baggett and Henningson1998). At this stage, the laminar boundary layer flow has started to break down to turbulence.

Figure 18. (a) Instantaneous isosurface of the ![]() $Q$-criterion coloured by contours of the streamwise velocity; (b) contour plot of the wall-shear stress show the formation of streaks before transition and
$Q$-criterion coloured by contours of the streamwise velocity; (b) contour plot of the wall-shear stress show the formation of streaks before transition and ![]() $(\eta,z)$ slices of instantaneous streamwise velocity contours along with contour lines of the
$(\eta,z)$ slices of instantaneous streamwise velocity contours along with contour lines of the ![]() $Q$-criteria.
$Q$-criteria.
6. Transition to turbulence
Our DNS study demonstrates that amplification of steady streaks, that result from quadratic interactions of oblique waves, leads to formation of a 3-D inflectional boundary layer profile. During this process, fluctuations with multiple spatial and temporal scales develop and, despite the periodic nature of upstream forcing, the flow downstream of reattachment becomes turbulent. In this section we utilize wall and boundary layer statistics to illustrate the onset of turbulence on the second wedge.
6.1. Wall statistics: skin friction
Boundary layer transition is characterized by a rapid increase in wall friction. Figure 19(a) utilizes instantaneous wall-shear distribution to identify transitional and turbulent regions. The wall-shear stress experiences sinuous-subharmonic modulation downstream of the reattachment (at ![]() $x=60$, i.e.
$x=60$, i.e. ![]() $Re_{x} = 8.2 \times 10^{5}$) and finer spanwise scales emerge after
$Re_{x} = 8.2 \times 10^{5}$) and finer spanwise scales emerge after ![]() $x=80$ (i.e.
$x=80$ (i.e. ![]() $Re_{x} \approx 11 \times 10^{5}$). As shown in figure 19(b), this location coincides with the highest value of time-averaged wall shear. Even though significant attenuation of spanwise variations of the wall-shear stress associated with the initial streaks takes place by
$Re_{x} \approx 11 \times 10^{5}$). As shown in figure 19(b), this location coincides with the highest value of time-averaged wall shear. Even though significant attenuation of spanwise variations of the wall-shear stress associated with the initial streaks takes place by ![]() $x = 80$, nonlinear interactions within the transition zone lead to the appearance of new streaks further downstream.
$x = 80$, nonlinear interactions within the transition zone lead to the appearance of new streaks further downstream.

Figure 19. Streamwise variations of (a) instantaneous and (b) time-averaged streamwise shear stresses as well as (c) wall skin-friction coefficient.
The spatial extent of the transition zone is visualized in figure 19(c) by showing streamwise development of the skin-friction coefficient,
 \begin{equation} C_{f} = \frac{1}{T}\frac{1}{L_{z}}\int_{0}^{T} \int_{0}^{L_{z}} \frac{\tau^{*}_{w}}{\frac{1}{2} \rho^*_{e} (U_{e}^{*})^2}\,\mathrm{d} z \,\mathrm{d} t. \end{equation}
\begin{equation} C_{f} = \frac{1}{T}\frac{1}{L_{z}}\int_{0}^{T} \int_{0}^{L_{z}} \frac{\tau^{*}_{w}}{\frac{1}{2} \rho^*_{e} (U_{e}^{*})^2}\,\mathrm{d} z \,\mathrm{d} t. \end{equation}
Here, ![]() $\tau ^*_{w}$ is the dimensional shear stress at the wall,
$\tau ^*_{w}$ is the dimensional shear stress at the wall, ![]() $\rho ^*_{e}$ and
$\rho ^*_{e}$ and ![]() $u^*_{e}$ are the dimensional density and streamwise velocity at the boundary layer edge,
$u^*_{e}$ are the dimensional density and streamwise velocity at the boundary layer edge, ![]() $L_{z}$ is the spanwise extent of the computational domain and
$L_{z}$ is the spanwise extent of the computational domain and ![]() $T = 4 L_{x}/u^*_{\infty }$. The values of
$T = 4 L_{x}/u^*_{\infty }$. The values of ![]() $C_{f}$ in laminar flows over a
$C_{f}$ in laminar flows over a ![]() $12$ degree wedge and over the double wedge are also plotted for comparison. The skin-friction coefficient drops because of flow separation but it grows again after reattachment. Near and downstream of reattachment, we observe a significant difference between laminar and turbulent values of
$12$ degree wedge and over the double wedge are also plotted for comparison. The skin-friction coefficient drops because of flow separation but it grows again after reattachment. Near and downstream of reattachment, we observe a significant difference between laminar and turbulent values of ![]() $C_f$. After
$C_f$. After ![]() $Re_{x} = 11.5 \times 10^{5}$, when
$Re_{x} = 11.5 \times 10^{5}$, when ![]() $C_f$ starts to decay with
$C_f$ starts to decay with ![]() $x$, the wall-friction coefficient is approximately seven times larger than its laminar counterpart. A comparison with the Van-Driest turbulent correlation for standard compressible boundary layers demonstrates that the flow on the second wedge is approaching fully developed turbulent values towards the end of the computational domain. In addition to skin friction, transition also has a significant impact on wall temperature. Additional details about the mean temperature and the wall statistics are included in Appendix F.
$x$, the wall-friction coefficient is approximately seven times larger than its laminar counterpart. A comparison with the Van-Driest turbulent correlation for standard compressible boundary layers demonstrates that the flow on the second wedge is approaching fully developed turbulent values towards the end of the computational domain. In addition to skin friction, transition also has a significant impact on wall temperature. Additional details about the mean temperature and the wall statistics are included in Appendix F.
6.2. Towards a turbulent compressible boundary layer
To illustrate the onset of turbulence, we also examine first- and second-order statistics in the latter stages of transition. At a given streamwise location, we report statistics in terms of the inner coordinate ![]() $\eta ^{+}$ that is obtained by non-dimensionalizing the wall-normal coordinate with the local viscous length
$\eta ^{+}$ that is obtained by non-dimensionalizing the wall-normal coordinate with the local viscous length ![]() $\delta _{\nu }$. Figure 20(a) shows the mean streamwise velocity
$\delta _{\nu }$. Figure 20(a) shows the mean streamwise velocity ![]() $u^{+}$ non-dimensionalized by the local friction velocity
$u^{+}$ non-dimensionalized by the local friction velocity ![]() $u_{\tau }$. The mean profile is obtained by averaging in time over
$u_{\tau }$. The mean profile is obtained by averaging in time over ![]() $2 L_{x}/u_{\infty }$ and in the spanwise direction over the extent of the computational domain
$2 L_{x}/u_{\infty }$ and in the spanwise direction over the extent of the computational domain ![]() $L_{z}$. In the presence of density variation along the compressible boundary layer, we utilize the Van-Driest transformation,
$L_{z}$. In the presence of density variation along the compressible boundary layer, we utilize the Van-Driest transformation,
 \begin{equation} u_{c}(\eta) = \int_{0}^{\langle{u}\rangle} \sqrt{\dfrac{\langle{\rho}\rangle}{\langle{\rho}\rangle_{w}}} \,\mathrm{d} \hat{u} = \int_{0}^{\eta}\sqrt{\dfrac{\langle{\rho}\rangle}{\langle{\rho}\rangle_{w}}} \, \frac{\partial \! \langle{u}\rangle}{\partial \hat{\eta}} \, \,\mathrm{d}\hat{\eta}, \end{equation}
\begin{equation} u_{c}(\eta) = \int_{0}^{\langle{u}\rangle} \sqrt{\dfrac{\langle{\rho}\rangle}{\langle{\rho}\rangle_{w}}} \,\mathrm{d} \hat{u} = \int_{0}^{\eta}\sqrt{\dfrac{\langle{\rho}\rangle}{\langle{\rho}\rangle_{w}}} \, \frac{\partial \! \langle{u}\rangle}{\partial \hat{\eta}} \, \,\mathrm{d}\hat{\eta}, \end{equation}
to compare the transitional velocity profiles with the ‘log law’ observed in incompressible turbulent boundary layers (White & Majdalani Reference White and Majdalani2006), where ![]() $\langle \,{\cdot }\,\rangle$ denotes averaging over time and spanwise direction, and
$\langle \,{\cdot }\,\rangle$ denotes averaging over time and spanwise direction, and ![]() $\langle {\rho }\rangle_{w}$ is the mean density at the wall. A fully developed turbulent boundary layer is characterized by the presence of the viscous sublayer close to the wall (
$\langle {\rho }\rangle_{w}$ is the mean density at the wall. A fully developed turbulent boundary layer is characterized by the presence of the viscous sublayer close to the wall (![]() $\eta ^{+} < 10$), where
$\eta ^{+} < 10$), where ![]() ${u^+_{c}} = \eta ^+$, and further away from the wall the mean velocity obeys the log law,
${u^+_{c}} = \eta ^+$, and further away from the wall the mean velocity obeys the log law,
where ![]() $\kappa = 0.41$ and
$\kappa = 0.41$ and ![]() $C = 5.2$.
$C = 5.2$.

Figure 20. The wall-normal profiles of mean (a) streamwise velocity and (b) temperature.
Figure 20(a) shows that the mean velocity in the boundary layer approaches the fully turbulent profile at ![]() $Re_{x} = 1.2\times 10^6$. Upstream of this location, within the transition zone, the boundary layer has a significantly greater momentum and most of it lies away from the wall. Furthermore, closer to the wall, the slope of the streamwise velocity profile is larger than the slope obtained using the viscous sublayer profile of a fully turbulent flow. This observation is consistent with the overshoot in skin-friction coefficient within the transition zone; cf. figure 19(b).
$Re_{x} = 1.2\times 10^6$. Upstream of this location, within the transition zone, the boundary layer has a significantly greater momentum and most of it lies away from the wall. Furthermore, closer to the wall, the slope of the streamwise velocity profile is larger than the slope obtained using the viscous sublayer profile of a fully turbulent flow. This observation is consistent with the overshoot in skin-friction coefficient within the transition zone; cf. figure 19(b).
In addition to the mean velocity, the mean temperature profile plays an important role in heat transfer and material response analysis of hypersonic flows. Walz's modified Crocco-Busemann relation,
is commonly used to describe the relation between temperature and velocity in a zero pressure gradient turbulent boundary layer. Here, ![]() $\langle {u_{e}}\rangle$ and
$\langle {u_{e}}\rangle$ and ![]() $\langle {T_{e}}\rangle$ denote the mean boundary layer edge velocity and temperature, respectively,
$\langle {T_{e}}\rangle$ denote the mean boundary layer edge velocity and temperature, respectively, ![]() $\langle {T_{r}}\rangle$ is the mean recovery temperature and, since the wall is adiabatic, the mean wall temperature is determined by
$\langle {T_{r}}\rangle$ is the mean recovery temperature and, since the wall is adiabatic, the mean wall temperature is determined by ![]() $\langle {T_{w}}\rangle = \langle {T_{r}}\rangle$. In spite of pressure variations post-reattachment, figure 20(b) demonstrates that the quadratic relation in (6.4) holds throughout the transition zone. As the flow approaches a fully turbulent profile, we see a slight deviation from this relation in the outer region away from the wall; this observation is in agreement with prior studies of fully turbulent compressible boundary layers (Duan, Beekman & Martín Reference Duan, Beekman and Martín2011; Franko & Lele Reference Franko and Lele2013).
$\langle {T_{w}}\rangle = \langle {T_{r}}\rangle$. In spite of pressure variations post-reattachment, figure 20(b) demonstrates that the quadratic relation in (6.4) holds throughout the transition zone. As the flow approaches a fully turbulent profile, we see a slight deviation from this relation in the outer region away from the wall; this observation is in agreement with prior studies of fully turbulent compressible boundary layers (Duan, Beekman & Martín Reference Duan, Beekman and Martín2011; Franko & Lele Reference Franko and Lele2013).
We next examine spatial development of flow fluctuations by evaluating second-order statistics and comparing them with those observed in a Mach 5 fully developed turbulent flat-plate boundary layer (Duan et al. Reference Duan, Beekman and Martín2011). Figure 21(a–c) shows the streamwise variation of the density-weighted r.m.s. values of the streamwise, wall-normal and spanwise velocity fluctuation components. In the transition zone we observe large values of fluctuations away from the wall in all three plots. Further downstream, at ![]() $Re_{x} = 1.2 \times 10^6$, the r.m.s. values closer to the wall are in agreement with fully turbulent values. However, away from the wall, the r.m.s. values of
$Re_{x} = 1.2 \times 10^6$, the r.m.s. values closer to the wall are in agreement with fully turbulent values. However, away from the wall, the r.m.s. values of ![]() $u'$ and
$u'$ and ![]() $w'$ deviate from the flat-plate profiles. We attribute this deviation to the presence of 3-D oblique waves and streaks that persist downstream because of continuous upstream forcing in our set-up.
$w'$ deviate from the flat-plate profiles. We attribute this deviation to the presence of 3-D oblique waves and streaks that persist downstream because of continuous upstream forcing in our set-up.

Figure 21. The wall-normal profiles of density weighted r.m.s. values of (a) streamwise, (b) wall-normal and (c) spanwise velocity fluctuations at different Reynolds numbers. (d) Energy spectrum as a function of spanwise wavenumber ![]() $\beta$ at
$\beta$ at ![]() $Re_{x} = 1.2 \times 10^6$.
$Re_{x} = 1.2 \times 10^6$.
To illustrate the broadband nature of velocity fluctuations in the later stages of transition, in figure 21(d) we evaluate the spanwise wavenumber dependence of the individual contributions of velocity fluctuations to the one-dimensional energy spectrum at ![]() $Re_{x} = 1.2 \times 10^{6}$ and
$Re_{x} = 1.2 \times 10^{6}$ and ![]() $\eta ^{+}=40$. At this location, the energy spectrum of streamwise velocity fluctuations clearly exhibits inertial and dissipative subrange features, indicating that the flow is approaching a fully turbulent stage.
$\eta ^{+}=40$. At this location, the energy spectrum of streamwise velocity fluctuations clearly exhibits inertial and dissipative subrange features, indicating that the flow is approaching a fully turbulent stage.
Our DNS also provides data for evaluating non-dimensional parameters which can be utilized for low-complexity modelling of high-speed compressible turbulent flows using time-averaged NS equations (Hirsch Reference Hirsch2007). In particular, we examine the spatial evolution of the fluctuation Mach number, ![]() $M_{t}$, the fluctuation Prandtl number,
$M_{t}$, the fluctuation Prandtl number, ![]() $Pr_t$, and Huang's modified strong Reynolds analogy parameter (Huang, Coleman & Bradshaw Reference Huang, Coleman and Bradshaw1995),
$Pr_t$, and Huang's modified strong Reynolds analogy parameter (Huang, Coleman & Bradshaw Reference Huang, Coleman and Bradshaw1995), ![]() $\psi _{sra}$,
$\psi _{sra}$,
 \begin{align} M_t = \sqrt{\frac{{\langle{u_i^\prime u_i^\prime}}\rangle}{\gamma \,R \langle{T}\rangle}}, \quad Pr_t = \frac{\langle{ u^\prime v^\prime}\rangle} {\langle{ v^\prime T^\prime}\rangle} \frac{\partial_{\eta} \! \langle{T}\rangle}{\partial_{\eta} \! \langle{u}\rangle},\quad \psi_{{sra}} = \frac{\left(1-\dfrac{\partial \langle{T_{0}}\rangle}{\partial \langle{T}\rangle}\right) \, Pr_t}{(\gamma-1)\langle{M}\rangle^2}\,\dfrac{\langle{u}\rangle}{\langle{T}\rangle}\,\frac{T'_{rms}}{u'_{rms}}. \end{align}
\begin{align} M_t = \sqrt{\frac{{\langle{u_i^\prime u_i^\prime}}\rangle}{\gamma \,R \langle{T}\rangle}}, \quad Pr_t = \frac{\langle{ u^\prime v^\prime}\rangle} {\langle{ v^\prime T^\prime}\rangle} \frac{\partial_{\eta} \! \langle{T}\rangle}{\partial_{\eta} \! \langle{u}\rangle},\quad \psi_{{sra}} = \frac{\left(1-\dfrac{\partial \langle{T_{0}}\rangle}{\partial \langle{T}\rangle}\right) \, Pr_t}{(\gamma-1)\langle{M}\rangle^2}\,\dfrac{\langle{u}\rangle}{\langle{T}\rangle}\,\frac{T'_{rms}}{u'_{rms}}. \end{align}
Here, ![]() $\langle {u_i^\prime u_i^\prime }\rangle = \langle {u^\prime u^\prime }\rangle + \langle {v^\prime v^\prime }\rangle + \langle {w^\prime w^\prime }\rangle$,
$\langle {u_i^\prime u_i^\prime }\rangle = \langle {u^\prime u^\prime }\rangle + \langle {v^\prime v^\prime }\rangle + \langle {w^\prime w^\prime }\rangle$, ![]() $\gamma$ and
$\gamma$ and ![]() $R$ denote the specific heat ratio and the gas constant, respectively, and
$R$ denote the specific heat ratio and the gas constant, respectively, and ![]() $T_{0}$ is the stagnation temperature. In a fully developed turbulent boundary layer,
$T_{0}$ is the stagnation temperature. In a fully developed turbulent boundary layer, ![]() $\psi _{sra}$ provides a measure of correlation between velocity and temperature fluctuations (Huang et al. Reference Huang, Coleman and Bradshaw1995).
$\psi _{sra}$ provides a measure of correlation between velocity and temperature fluctuations (Huang et al. Reference Huang, Coleman and Bradshaw1995).
Figure 22 shows that towards the end of the computational domain, at ![]() $Re_x= 1.2\times 10^{6}$, these parameters are close to those observed in canonical hypersonic boundary layers, i.e.
$Re_x= 1.2\times 10^{6}$, these parameters are close to those observed in canonical hypersonic boundary layers, i.e. ![]() $M_t \approx 0.2-0.3$,
$M_t \approx 0.2-0.3$, ![]() $Pr_{t} \approx 0.9$ and
$Pr_{t} \approx 0.9$ and ![]() $\psi _{{sra}} \approx 1$ (Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011). However, upstream of the breakdown region, at
$\psi _{{sra}} \approx 1$ (Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011). However, upstream of the breakdown region, at ![]() $Re_x= 1.0\times 10^{6}$, there is a significant deviation compared with these canonical values. Here,
$Re_x= 1.0\times 10^{6}$, there is a significant deviation compared with these canonical values. Here, ![]() $M_t$ becomes as high as
$M_t$ becomes as high as ![]() $0.45$ which suggests that compressibility effects on flow fluctuations cannot be neglected in the transition zone. Similarly,
$0.45$ which suggests that compressibility effects on flow fluctuations cannot be neglected in the transition zone. Similarly, ![]() $Pr_t$ can reach values close to
$Pr_t$ can reach values close to ![]() $1.5$ that correspond to decreased fluctuation temperature fluxes in the breakdown region. Furthermore,
$1.5$ that correspond to decreased fluctuation temperature fluxes in the breakdown region. Furthermore, ![]() $Pr_t$ exhibits large variations away from the wall, which is in contrast to the observations in flat-plate turbulent boundary layers, where
$Pr_t$ exhibits large variations away from the wall, which is in contrast to the observations in flat-plate turbulent boundary layers, where ![]() $Pr_t$ has a value of
$Pr_t$ has a value of ![]() $0.9$ throughout the boundary layer (Saffman & Wilcox Reference Saffman and Wilcox1974; Smith & Smits Reference Smith and Smits1993; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011). Similar deviations from canonical values in the outer region of the boundary layer are also observed in
$0.9$ throughout the boundary layer (Saffman & Wilcox Reference Saffman and Wilcox1974; Smith & Smits Reference Smith and Smits1993; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011). Similar deviations from canonical values in the outer region of the boundary layer are also observed in ![]() $\psi _{sra}$. We conjecture that, in the presence of persistent upstream excitations, the resulting unsteady fluctuations are primarily responsible for these discrepancies.
$\psi _{sra}$. We conjecture that, in the presence of persistent upstream excitations, the resulting unsteady fluctuations are primarily responsible for these discrepancies.

Figure 22. The wall-normal profiles of (a) the fluctuation Mach number, ![]() $M_t$; (b) the fluctuation Prandtl number,
$M_t$; (b) the fluctuation Prandtl number, ![]() $Pr_t$; and (c) Huang's modified strong Reynolds analogy parameter,
$Pr_t$; and (c) Huang's modified strong Reynolds analogy parameter, ![]() $\psi _{sra}$.
$\psi _{sra}$.
7. Concluding remarks
Axisymmetric cone-flare experiments (Benitez et al. Reference Benitez, Esquieu, Jewell and Schneider2020; Butler & Laurence Reference Butler and Laurence2021) identified unsteady fluctuations in the separation zone and it is believed that these play an important role in initiating hypersonic flow transition. As demonstrated in figure 23, we observe a strong qualitative similarity between the spatial structures of fluctuations observed using schlieren measurements in a Mach ![]() $6$ reattaching flow on axisymmetric cone-flare (Butler & Laurence Reference Butler and Laurence2021) and dominant oblique density fluctuations that we identify via resolvent analysis of separated flow over a slender double wedge. Inspired by these observations, we have examined transition mechanisms in a Mach
$6$ reattaching flow on axisymmetric cone-flare (Butler & Laurence Reference Butler and Laurence2021) and dominant oblique density fluctuations that we identify via resolvent analysis of separated flow over a slender double wedge. Inspired by these observations, we have examined transition mechanisms in a Mach ![]() $5$ hypersonic flow over a slender double-wedge subject to unsteady upstream disturbances.
$5$ hypersonic flow over a slender double-wedge subject to unsteady upstream disturbances.

Figure 23. Qualitative comparison of spatial structures of (a) unsteady fluctuations observed using schlieren measurements in a Mach ![]() $6$ reattaching flow on axisymmetric cone-flare at
$6$ reattaching flow on axisymmetric cone-flare at ![]() $U_{\infty }/\nu _{\infty } = 3 \times 10^{6} \, \mathrm {m}^{-1}$ (Butler & Laurence Reference Butler and Laurence2021); and (b) dominant oblique density fluctuations resulting from input–output analysis of linearization around a laminar 2-D Mach
$U_{\infty }/\nu _{\infty } = 3 \times 10^{6} \, \mathrm {m}^{-1}$ (Butler & Laurence Reference Butler and Laurence2021); and (b) dominant oblique density fluctuations resulting from input–output analysis of linearization around a laminar 2-D Mach ![]() $5$ reattaching flow at
$5$ reattaching flow at ![]() $U_{\infty }/\nu _{\infty } = 13.6 \times 10^{6} \, \mathrm {m}^{-1}$.
$U_{\infty }/\nu _{\infty } = 13.6 \times 10^{6} \, \mathrm {m}^{-1}$.
To investigate the early stages of transition, we employ resolvent analysis to evaluate responses of the laminar 2-D base flow to exogenous time-periodic inputs. This allows us to identify prevailing spatio-temporal scales, the spatial structure of disturbances that most effectively excite the double-wedge flow, as well as the spatial structure of the resulting responses and the underlying physical mechanisms. In the presence of flow separation, our analysis shows that two types of disturbances are strongly amplified by the linearized dynamics: steady streamwise vortices and unsteady oblique waves. While amplification of steady upstream vortical disturbances has been studied in Dwivedi et al. (Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), oblique waves that amplify within the separation–reattachment zone have not been investigated. Recently, Lugrin et al. (Reference Lugrin, Beneddine, Leclercq, Garnier and Bur2021) examined the growth of unsteady perturbations that arise from the ‘first mode’ instability of an axisymmetric boundary layer over cylinder-flare geometry. In the presence of stochastic disturbances in the inlet of the computational domain, DNS was used to demonstrate that oblique waves that emerge in the upstream boundary layer (i.e. before separation) can undergo nonlinear interactions similar to those observed in attached compressible boundary layers (Chang & Malik Reference Chang and Malik1994; Mayer et al. Reference Mayer, Von Terzi and Fasel2011) and cause transition in separated high-speed flows (Lugrin et al. Reference Lugrin, Beneddine, Leclercq, Garnier and Bur2021). In contrast, we show that unsteady disturbances that are localized upstream of the corner trigger oblique waves downstream of the corner even in the absence of local or global boundary layer instabilities. These oblique waves experience significant amplification within the separation–reattachment zone and their role in initiating transition in flows with SWBLI has not been studied before.
By carrying out resolvent analysis of the linearized flow equations subject to disturbances that are introduced in a plane immediately upstream of separation, we identify the physical mechanism responsible for non-modal amplification of oblique waves in the presence of flow separation. The subsequent nonlinear interaction of dominant unsteady oblique fluctuations is examined using a weakly nonlinear analysis to demonstrate the emergence of steady reattachment streaks inside the recirculation bubble. Direct numerical simulation confirms the predictions of our analysis and provides a detailed characterization of transition initiated by time-periodic upstream oblique disturbances.
Next we briefly summarize our main contributions as follows.
(i) Amplification of oblique waves by base flow curvature: We analyse the fluctuations’ kinetic energy in a streamline-aligned orthogonal coordinate system to identify physical mechanisms responsible for amplification of oblique waves in the separation zone. Large energy amplification arises from the growth of the fluctuation shear stress due to streamline curvature in the separated shear layer. This is in contrast to the attached boundary layers, where no such mechanism exists. To compare separated and attached boundary layers, we also conduct resolvent analysis of the flow over a wedge that does not contain the compression corner (this wedge is identical to the first wedge in the double-wedge configuration analysed in the paper). Figure 24 demonstrates that the presence of a recirculation zone in the double-wedge flow significantly increases amplification relative to the single-wedge flow. The amplification profiles of the fluctuation shear stresses differ in these two cases because of fundamentally different physical mechanisms.
(ii) Steady reattachment streaks through base flow deceleration: We utilize a weakly nonlinear analysis to show that the resolvent operator associated with the linearized dynamics governs the evolution of steady streaks that arise from quadratic interactions of unsteady oblique waves. Vortical excitations in the reattaching shear layer generated by these interactions lead to the formation of streaks in the recirculation zone and their subsequent amplification downstream. Additionally, we use SVD of the resolvent operator to demonstrate that secondary reattachment streaks are well approximated by the second output resolvent mode. Similar to the most amplified steady output in compression ramp flow (Dwivedi et al. Reference Dwivedi, Sidharth, Nichols, Candler and Jovanović2019), our analysis of the energy budget shows that deceleration of the laminar base flow near reattachment is responsible for amplification of reattachment streaks associated with this sub-optimal mode.
(iii) Transition to turbulence: We use DNS to examine nonlinear stages of the evolution of flow fluctuations. In the presence of strong upstream oblique disturbances, steady streaks saturate after reattachment and experience sinuous subharmonic oscillations. The resulting 3-D boundary layer breaks down further downstream and the observed flow structures are similar to those in other canonical configurations: nonlinear interactions of streaks with oblique waves lead to the development of staggered patterns of lambda vortices, followed by a rapid emergence of higher harmonics in fluctuations and multiple inflection points in the mean velocity profile before breakdown to turbulence (see, e.g. Hall & Horseman Reference Hall and Horseman1991; Yu & Liu Reference Yu and Liu1994; Reddy et al. Reference Reddy, Schmid, Baggett and Henningson1998). As the flow transitions to turbulence, the wall friction increases rapidly before settling to the values predicted by turbulent correlations. Within the transitional zone, non-dimensional parameters that are critical for modelling temperature and compressibility effects in high-speed turbulent flows (Hirsch Reference Hirsch2007), e.g. the fluctuation Prandtl and Mach numbers, significantly differ from their fully developed turbulent values. Post-breakdown, the boundary layer develops mean and fluctuation statistics that agree well with observations made in attached hypersonic turbulent boundary layers, thereby demonstrating the efficacy of unsteady oblique waves in triggering transition in separated high-speed boundary layer flows.

Figure 24. The streamwise evolution of (a) streamwise specific energy and (b) fluctuation shear stress of the dominant output mode ![]() ${\boldsymbol {\phi }}_1$ of the resolvent associated with linearization around laminar flows over double and single wedges with (
${\boldsymbol {\phi }}_1$ of the resolvent associated with linearization around laminar flows over double and single wedges with (![]() $\omega = 0.4,\lambda _{z} = 3.0$).
$\omega = 0.4,\lambda _{z} = 3.0$).
Unsteady disturbances in hypersonic boundary layers can arise from free-stream turbulence in wind tunnel experiments (Schneider Reference Schneider2001, Reference Schneider2015), interactions of unsteady free-stream disturbances with surface roughness (Wu Reference Wu2001; Gonzalez & Wu Reference Gonzalez and Wu2019), atmospheric particulates associated with ice clouds and volcanic dust (Turco Reference Turco1992; Chuvakhov, Fedorov & Obraz Reference Chuvakhov, Fedorov and Obraz2019) and atmospheric turbulence (Bushnell Reference Bushnell1990). Novel physical mechanisms that we identify are unique to high-speed boundary layers with a separation–reattachment zone. We expect that insights about transition mechanisms that we provide using a combination of resolvent and weakly nonlinear analyses with DNS will motivate a systematic evaluation of specific disturbance environments that appear in wind tunnels or free flights and guide the development of low-complexity models for the fast and accurate prediction of transition in hypersonic flows under realistic in-flight conditions.
Acknowledgements
We would like to thank Professor G.V. Candler for providing access to the US3D solver and computational facilities at the University of Minnesota.
Funding
This work has been supported by the Air Force Office of Scientific Research under award FA9550-18-1-0422.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Nonlinear terms at  ${O}(\epsilon ^2)$
${O}(\epsilon ^2)$
As shown in § 4.1, ![]() $\hat {\boldsymbol {d}}_{0}^{(2)} \mathrel {\mathop :}= \mathcal {N}_{0}^{(2)}(\hat {{\boldsymbol {\psi }}}^{(1)}_{\pm })$ accounts for quadratic interactions between
$\hat {\boldsymbol {d}}_{0}^{(2)} \mathrel {\mathop :}= \mathcal {N}_{0}^{(2)}(\hat {{\boldsymbol {\psi }}}^{(1)}_{\pm })$ accounts for quadratic interactions between ![]() $\hat {{\boldsymbol {\psi }}}^{(1)}_{+}$ and
$\hat {{\boldsymbol {\psi }}}^{(1)}_{+}$ and ![]() $\hat {{\boldsymbol {\psi }}}^{(1)}_{-}$ at
$\hat {{\boldsymbol {\psi }}}^{(1)}_{-}$ at ![]() ${O}(\epsilon ^2)$. For steady streaks
${O}(\epsilon ^2)$. For steady streaks ![]() $\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$,
$\hat {{\boldsymbol {\psi }}}^{(2)}_{0}$, ![]() $\hat {\boldsymbol {d}}^{(2)}_{0,\rho } = 0$ and the contributions to the equations for the momentum and total energy fluctuations are given by
$\hat {\boldsymbol {d}}^{(2)}_{0,\rho } = 0$ and the contributions to the equations for the momentum and total energy fluctuations are given by
 \begin{align} \hat{\boldsymbol{d}}^{(2)}_{0,\rho u} & = \left(\gamma-1\right) \dfrac{\partial}{\partial x} \bar{\rho} \left(\dfrac{\gamma - 3}{\gamma - 1} (u_{+}^{(1)}u_{-}^{(1)})+ (v_{+}^{(1)} v_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ & \quad - \dfrac{\partial}{\partial y} \bar{\rho} \left(u_{-}^{(1)}v_{+}^{(1)}+ u_{+}^{(1)} v_{-}^{(1)} \right) \,-\, \mathrm{i} \beta \bar{\rho} \left(u_{-}^{(1)}w_{+}^{(1)}+ u_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,\rho v} & = \left(\gamma-1\right) \dfrac{\partial}{\partial y} \bar{\rho} \left(\dfrac{\gamma - 3}{\gamma - 1} (v_{+}^{(1)}v_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad- \dfrac{\partial}{\partial x} \bar{\rho} \left(u_{-}^{(1)}v_{+}^{(1)}+ u_{+}^{(1)} v_{-}^{(1)} \right) \,-\, \mathrm{i} \beta \bar{\rho} \left(v_{-}^{(1)}w_{+}^{(1)}+ v_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,\rho w} & = \mathrm{i} \beta \bar{\rho} \left(\gamma-1\right) \left(\dfrac{\gamma - 3}{\gamma - 1} (w_{+}^{(1)}w_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (v_{+}^{(1)} v_{-}^{(1)}) \right) \nonumber\\ &\quad - \dfrac{\partial}{\partial x} \bar{\rho} \left(u_{-}^{(1)}w_{+}^{(1)}+ u_{+}^{(1)} w_{-}^{(1)} \right) \,-\, \dfrac{\partial}{\partial y} \bar{\rho} \left(v_{-}^{(1)}w_{+}^{(1)}+ v_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,E_{t}} & ={-} \mathrm{i} \beta \bar{\rho}\, w_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{u} u_{-}^{(1)} + \bar{v} v_{-}^{(1)}\right) \nonumber\\ &\quad- \phantom{-} \mathrm{i} \beta \bar{\rho}\, w_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{u} u_{+}^{(1)} + \bar{v} v_{+}^{(1)}\right) \nonumber\\ &\quad - \left(\gamma-1\right) \dfrac{\partial}{\partial x} \bar{\rho} \bar{u} \left(\dfrac{\gamma - 3}{\gamma - 1} (u_{+}^{(1)}u_{-}^{(1)})+ (v_{+}^{(1)} v_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad + \left(\gamma-1\right) \dfrac{\partial}{\partial y} \bar{\rho} \bar{v} \left(\dfrac{\gamma - 3}{\gamma - 1} (v_{+}^{(1)}v_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad- \dfrac{\partial}{\partial x}\bar{\rho}\, u_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{v} v_{-}^{(1)}\right) \,-\, \dfrac{\partial}{\partial x}\bar{\rho}\, u_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{v} v_{+}^{(1)}\right) \nonumber\\ &\quad - \dfrac{\partial}{\partial y}\bar{\rho}\, v_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{u} u_{-}^{(1)}\right) \,-\, \dfrac{\partial}{\partial y}\bar{\rho}\, v_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{u} u_{+}^{(1)}\right) \nonumber\\ &\quad -\mathrm{i} \beta \lambda \left( w^{(1)}_{+} \dfrac{\partial}{\partial x} u^{(1)}_{-} + w^{(1)}_{-} \dfrac{\partial}{\partial x} u^{(1)}_{+}\right) + \mathrm{i} \beta \mu \left( u^{(1)}_{+} \dfrac{\partial}{\partial x} w^{(1)}_{-} + u^{(1)}_{-} \dfrac{\partial}{\partial x} w^{(1)}_{+}\right) \nonumber\\ &\quad - \mathrm{i} \beta \lambda \left( w^{(1)}_{+} \dfrac{\partial}{\partial y} y^{(1)}_{-} + w^{(1)}_{-} \dfrac{\partial}{\partial y} v^{(1)}_{+}\right) + \mathrm{i} \beta \mu \left( v^{(1)}_{+} \dfrac{\partial}{\partial y} w^{(1)}_{-} + v^{(1)}_{-} \dfrac{\partial}{\partial y} w^{(1)}_{+}\right) \nonumber\\ &\quad -2 \beta^{2} \mu \left( u^{(1)}_{+} u^{(1)}_{-} + v^{(1)}_{+} v^{(1)}_{-} + \dfrac{\lambda+2\mu}{\mu} w^{(1)}_{+} w^{(1)}_{-} \right) \nonumber\\ &\quad+ \mathrm{i} 2 \beta \dfrac{\partial}{\partial y} \left((\mu+\lambda) (w^{(1)}_{+} v^{(1)}_{-} + w^{(1)}_{-} v^{(1)}_{+}) \right) \nonumber\\ &\quad+ \mathrm{i} 2 \beta \dfrac{\partial}{\partial x} \left((\mu+\lambda) (w^{(1)}_{+} u^{(1)}_{-} + w^{(1)}_{-} u^{(1)}_{+}) \right) \nonumber\\ &\quad + \dfrac{\partial}{\partial x} \mu \left(v^{(1)}_{+} \dfrac{\partial u^{(1)}_{-}}{\partial y} + v^{(1)}_{-} \dfrac{\partial u^{(1)}_{+}}{\partial y} \right) + \dfrac{\partial}{\partial x} \lambda \left(u^{(1)}_{+} \dfrac{\partial v^{(1)}_{-}}{\partial y} + u^{(1)}_{-} \dfrac{\partial v^{(1)}_{+}}{\partial y} \right) \nonumber\\ &\quad+ \dfrac{\partial}{\partial y} \mu \left(u^{(1)}_{+} \dfrac{\partial v^{(1)}_{-}}{\partial x} + u^{(1)}_{-} \dfrac{\partial v^{(1)}_{+}}{\partial x} \right) + \dfrac{\partial}{\partial y} \lambda \left(v^{(1)}_{+} \dfrac{\partial u^{(1)}_{-}}{\partial x} + v^{(1)}_{-} \dfrac{\partial u^{(1)}_{+}}{\partial x} \right) \nonumber\\ &\quad+\dfrac{\partial}{\partial x} \mu \left(\dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial x} + \dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial x} + \dfrac{\lambda+2\mu}{\mu} \dfrac{\partial u^{(1)}_{+} u^{(1)}_{-}}{\partial x} \right) \nonumber\\ &\quad + \dfrac{\partial}{\partial y} \mu \left(\dfrac{\partial u^{(1)}_{+} u^{(1)}_{-}}{\partial y} + \dfrac{\partial w^{(1)}_{+} w^{(1)}_{-}}{\partial y} + \dfrac{\lambda+2\mu}{\mu} \dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial y} \right), \end{align}
\begin{align} \hat{\boldsymbol{d}}^{(2)}_{0,\rho u} & = \left(\gamma-1\right) \dfrac{\partial}{\partial x} \bar{\rho} \left(\dfrac{\gamma - 3}{\gamma - 1} (u_{+}^{(1)}u_{-}^{(1)})+ (v_{+}^{(1)} v_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ & \quad - \dfrac{\partial}{\partial y} \bar{\rho} \left(u_{-}^{(1)}v_{+}^{(1)}+ u_{+}^{(1)} v_{-}^{(1)} \right) \,-\, \mathrm{i} \beta \bar{\rho} \left(u_{-}^{(1)}w_{+}^{(1)}+ u_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,\rho v} & = \left(\gamma-1\right) \dfrac{\partial}{\partial y} \bar{\rho} \left(\dfrac{\gamma - 3}{\gamma - 1} (v_{+}^{(1)}v_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad- \dfrac{\partial}{\partial x} \bar{\rho} \left(u_{-}^{(1)}v_{+}^{(1)}+ u_{+}^{(1)} v_{-}^{(1)} \right) \,-\, \mathrm{i} \beta \bar{\rho} \left(v_{-}^{(1)}w_{+}^{(1)}+ v_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,\rho w} & = \mathrm{i} \beta \bar{\rho} \left(\gamma-1\right) \left(\dfrac{\gamma - 3}{\gamma - 1} (w_{+}^{(1)}w_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (v_{+}^{(1)} v_{-}^{(1)}) \right) \nonumber\\ &\quad - \dfrac{\partial}{\partial x} \bar{\rho} \left(u_{-}^{(1)}w_{+}^{(1)}+ u_{+}^{(1)} w_{-}^{(1)} \right) \,-\, \dfrac{\partial}{\partial y} \bar{\rho} \left(v_{-}^{(1)}w_{+}^{(1)}+ v_{+}^{(1)} w_{-}^{(1)} \right),\nonumber\\ \hat{\boldsymbol{d}}^{(2)}_{0,E_{t}} & ={-} \mathrm{i} \beta \bar{\rho}\, w_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{u} u_{-}^{(1)} + \bar{v} v_{-}^{(1)}\right) \nonumber\\ &\quad- \phantom{-} \mathrm{i} \beta \bar{\rho}\, w_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{u} u_{+}^{(1)} + \bar{v} v_{+}^{(1)}\right) \nonumber\\ &\quad - \left(\gamma-1\right) \dfrac{\partial}{\partial x} \bar{\rho} \bar{u} \left(\dfrac{\gamma - 3}{\gamma - 1} (u_{+}^{(1)}u_{-}^{(1)})+ (v_{+}^{(1)} v_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad + \left(\gamma-1\right) \dfrac{\partial}{\partial y} \bar{\rho} \bar{v} \left(\dfrac{\gamma - 3}{\gamma - 1} (v_{+}^{(1)}v_{-}^{(1)})+ (u_{+}^{(1)} u_{-}^{(1)}) + (w_{+}^{(1)} w_{-}^{(1)}) \right) \nonumber\\ &\quad- \dfrac{\partial}{\partial x}\bar{\rho}\, u_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{v} v_{-}^{(1)}\right) \,-\, \dfrac{\partial}{\partial x}\bar{\rho}\, u_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{v} v_{+}^{(1)}\right) \nonumber\\ &\quad - \dfrac{\partial}{\partial y}\bar{\rho}\, v_{+}^{(1)} \left(\gamma{C_v} T_{-}^{(1)} + \bar{u} u_{-}^{(1)}\right) \,-\, \dfrac{\partial}{\partial y}\bar{\rho}\, v_{-}^{(1)} \left(\gamma{C_v} T_{+}^{(1)} + \bar{u} u_{+}^{(1)}\right) \nonumber\\ &\quad -\mathrm{i} \beta \lambda \left( w^{(1)}_{+} \dfrac{\partial}{\partial x} u^{(1)}_{-} + w^{(1)}_{-} \dfrac{\partial}{\partial x} u^{(1)}_{+}\right) + \mathrm{i} \beta \mu \left( u^{(1)}_{+} \dfrac{\partial}{\partial x} w^{(1)}_{-} + u^{(1)}_{-} \dfrac{\partial}{\partial x} w^{(1)}_{+}\right) \nonumber\\ &\quad - \mathrm{i} \beta \lambda \left( w^{(1)}_{+} \dfrac{\partial}{\partial y} y^{(1)}_{-} + w^{(1)}_{-} \dfrac{\partial}{\partial y} v^{(1)}_{+}\right) + \mathrm{i} \beta \mu \left( v^{(1)}_{+} \dfrac{\partial}{\partial y} w^{(1)}_{-} + v^{(1)}_{-} \dfrac{\partial}{\partial y} w^{(1)}_{+}\right) \nonumber\\ &\quad -2 \beta^{2} \mu \left( u^{(1)}_{+} u^{(1)}_{-} + v^{(1)}_{+} v^{(1)}_{-} + \dfrac{\lambda+2\mu}{\mu} w^{(1)}_{+} w^{(1)}_{-} \right) \nonumber\\ &\quad+ \mathrm{i} 2 \beta \dfrac{\partial}{\partial y} \left((\mu+\lambda) (w^{(1)}_{+} v^{(1)}_{-} + w^{(1)}_{-} v^{(1)}_{+}) \right) \nonumber\\ &\quad+ \mathrm{i} 2 \beta \dfrac{\partial}{\partial x} \left((\mu+\lambda) (w^{(1)}_{+} u^{(1)}_{-} + w^{(1)}_{-} u^{(1)}_{+}) \right) \nonumber\\ &\quad + \dfrac{\partial}{\partial x} \mu \left(v^{(1)}_{+} \dfrac{\partial u^{(1)}_{-}}{\partial y} + v^{(1)}_{-} \dfrac{\partial u^{(1)}_{+}}{\partial y} \right) + \dfrac{\partial}{\partial x} \lambda \left(u^{(1)}_{+} \dfrac{\partial v^{(1)}_{-}}{\partial y} + u^{(1)}_{-} \dfrac{\partial v^{(1)}_{+}}{\partial y} \right) \nonumber\\ &\quad+ \dfrac{\partial}{\partial y} \mu \left(u^{(1)}_{+} \dfrac{\partial v^{(1)}_{-}}{\partial x} + u^{(1)}_{-} \dfrac{\partial v^{(1)}_{+}}{\partial x} \right) + \dfrac{\partial}{\partial y} \lambda \left(v^{(1)}_{+} \dfrac{\partial u^{(1)}_{-}}{\partial x} + v^{(1)}_{-} \dfrac{\partial u^{(1)}_{+}}{\partial x} \right) \nonumber\\ &\quad+\dfrac{\partial}{\partial x} \mu \left(\dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial x} + \dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial x} + \dfrac{\lambda+2\mu}{\mu} \dfrac{\partial u^{(1)}_{+} u^{(1)}_{-}}{\partial x} \right) \nonumber\\ &\quad + \dfrac{\partial}{\partial y} \mu \left(\dfrac{\partial u^{(1)}_{+} u^{(1)}_{-}}{\partial y} + \dfrac{\partial w^{(1)}_{+} w^{(1)}_{-}}{\partial y} + \dfrac{\lambda+2\mu}{\mu} \dfrac{\partial v^{(1)}_{+} v^{(1)}_{-}}{\partial y} \right), \end{align}
where we drop the caret notation on the right-hand side of (A1) for brevity. Here, ![]() $C_{v} = R/(\gamma -1)$, where
$C_{v} = R/(\gamma -1)$, where ![]() $R$ is the gas constant,
$R$ is the gas constant, ![]() $\gamma = 1.4$ is the ratio of the specific heat capacities, and
$\gamma = 1.4$ is the ratio of the specific heat capacities, and ![]() $\mu (x,y)$ and
$\mu (x,y)$ and ![]() $\lambda (x,y)$ are the coefficients of viscosity and bulk viscosity, respectively. We utilize Sutherland's law for computing viscosity and assume that
$\lambda (x,y)$ are the coefficients of viscosity and bulk viscosity, respectively. We utilize Sutherland's law for computing viscosity and assume that ![]() $\lambda =-{2 \mu }/{3}$.
$\lambda =-{2 \mu }/{3}$.
Appendix B. Relation between the state  $\varPsi$ and the output
$\varPsi$ and the output  $\varPhi$
$\varPhi$
Herein, we utilize a weakly nonlinear expansion to establish the relation between the components of the state vector ![]() ${\boldsymbol {\varPsi }} = (\varPsi _1, {\boldsymbol {\varPsi }}_{2}, \varPsi _3) \mathrel {\mathop :}= (\rho, \rho \boldsymbol{u}, E_t)$ in conserved variables and the components of the vector
${\boldsymbol {\varPsi }} = (\varPsi _1, {\boldsymbol {\varPsi }}_{2}, \varPsi _3) \mathrel {\mathop :}= (\rho, \rho \boldsymbol{u}, E_t)$ in conserved variables and the components of the vector ![]() ${\boldsymbol {\varPhi }} = (\varPhi _1, {\boldsymbol {\varPhi }}_{2}, \varPhi _3) \mathrel {\mathop :}= (\rho, \boldsymbol {u}, T)$ in primitive variables. Here,
${\boldsymbol {\varPhi }} = (\varPhi _1, {\boldsymbol {\varPhi }}_{2}, \varPhi _3) \mathrel {\mathop :}= (\rho, \boldsymbol {u}, T)$ in primitive variables. Here, ![]() $E_t$ is the total energy per unit volume of the gas,
$E_t$ is the total energy per unit volume of the gas,
![]() $C_v$ is the specific heat at constant volume and
$C_v$ is the specific heat at constant volume and ![]() $| \boldsymbol {u} |^2 \mathrel {\mathop :}= \boldsymbol {u}^T \boldsymbol {u}$. Within the weakly nonlinear framework, we can decompose
$| \boldsymbol {u} |^2 \mathrel {\mathop :}= \boldsymbol {u}^T \boldsymbol {u}$. Within the weakly nonlinear framework, we can decompose ![]() ${\boldsymbol {\varPsi }}$ and
${\boldsymbol {\varPsi }}$ and ![]() ${\boldsymbol {\varPhi }}$ into the sums of base and fluctuating components,
${\boldsymbol {\varPhi }}$ into the sums of base and fluctuating components,
 \begin{equation} \left. \begin{aligned} {\boldsymbol{\varPsi}} & = \bar{{\boldsymbol{\varPsi}}} + {\boldsymbol{\psi}} =\bar{{\boldsymbol{\varPsi}}} + \epsilon {\boldsymbol{\psi}}^{(1)} +\epsilon^2 {\boldsymbol{\psi}}^{(2)} + {O} (\epsilon^3),\\ {\boldsymbol{\varPhi}} & = \bar{{\boldsymbol{\varPhi}}} + {\boldsymbol{\phi}} =\bar{{\boldsymbol{\varPhi}}} + \epsilon {\boldsymbol{\phi}}^{(1)} +\epsilon^2 {\boldsymbol{\phi}}^{(2)} + {O} (\epsilon^3), \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} {\boldsymbol{\varPsi}} & = \bar{{\boldsymbol{\varPsi}}} + {\boldsymbol{\psi}} =\bar{{\boldsymbol{\varPsi}}} + \epsilon {\boldsymbol{\psi}}^{(1)} +\epsilon^2 {\boldsymbol{\psi}}^{(2)} + {O} (\epsilon^3),\\ {\boldsymbol{\varPhi}} & = \bar{{\boldsymbol{\varPhi}}} + {\boldsymbol{\phi}} =\bar{{\boldsymbol{\varPhi}}} + \epsilon {\boldsymbol{\phi}}^{(1)} +\epsilon^2 {\boldsymbol{\phi}}^{(2)} + {O} (\epsilon^3), \end{aligned} \right\} \end{equation}
and utilize the following relations between the components of ![]() ${\boldsymbol {\varPsi }}$ and
${\boldsymbol {\varPsi }}$ and ![]() ${\boldsymbol {\varPhi }}$,
${\boldsymbol {\varPhi }}$,
 \begin{equation} \left. \begin{aligned} \varPsi_1 & = \varPhi_1,\\ {\boldsymbol{\varPsi}}_2 & = \varPhi_1 {\boldsymbol{\varPhi}}_2,\\ \varPsi_3 & = C_v \varPhi_1 \varPhi_3 + \dfrac{1}{2} \, \varPhi_1 | {\boldsymbol{\varPhi}}_2 |^2, \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \varPsi_1 & = \varPhi_1,\\ {\boldsymbol{\varPsi}}_2 & = \varPhi_1 {\boldsymbol{\varPhi}}_2,\\ \varPsi_3 & = C_v \varPhi_1 \varPhi_3 + \dfrac{1}{2} \, \varPhi_1 | {\boldsymbol{\varPhi}}_2 |^2, \end{aligned} \right\} \end{equation}to obtain
 \begin{equation} \left. \begin{aligned} {O(1):} & \quad \bar{\varPhi}_1 = \bar{\varPsi}_1, \quad \bar{{\boldsymbol{\varPhi}}}_2 = \dfrac{\bar{{\boldsymbol{\varPsi}}}_2}{\bar{\varPsi}_1}, \quad \bar{{\boldsymbol{\varPhi}}}_3 = \dfrac{1}{C_v \bar{\varPsi}_1} \left( \bar{\varPsi}_3 - \dfrac{| \bar{{\boldsymbol{\varPsi}}}_2 |^2}{2 \bar{\varPsi}_1}\right),\\ {O(\epsilon):} & \quad \left[ \begin{array}{c} {\phi^{(1)}_{1}} \\ {{\boldsymbol{\phi}}^{(1)}_{2}} \\ \phi^{(1)}_{3} \end{array} \right] =\underbrace{\dfrac{1}{\bar{\varPhi}_{1}} \! \left[ \begin{array}{ccc} \bar{\varPhi}_{1} & 0 & 0 \\ -\bar{{\boldsymbol{\varPhi}}}_{2} & I & 0 \\ \dfrac{1}{2 C_{v}} \, | \bar{{\boldsymbol{\varPhi}}}_{2} |^2 - \bar{\varPhi}_{3} & -\dfrac{1}{C_{v}} \, \bar{{\boldsymbol{\varPhi}}}_{2}^T & \dfrac{1}{C_{v}} \end{array} \right]}_{\mathcal{C}} \left[ \begin{array}{c} {\psi^{(1)}_{1}} \\ {{\boldsymbol{\psi}}^{(1)}_{2}} \\ {\psi^{(1)}_{3}} \end{array} \right],\\ {O(\epsilon^2):} & \quad \left[ \begin{array}{c} {\phi^{(2)}_{1}} \\ {{\boldsymbol{\phi}}^{(2)}_{2}} \\ \phi^{(2)}_{3} \end{array} \right] = \mathcal{C} \left[ \begin{array}{c} {\psi^{(2)}_{1}} \\ {{\boldsymbol{\psi}}^{(2)}_{2}} \\ \psi^{(2)}_{3} \end{array} \right] + \underbrace{\dfrac{1}{\bar{\varPhi}_{1}} \! \left[ \begin{array}{cc} 0 & 0 \\ I & 0 \\ 0 & \dfrac{1}{2 C_{v}} \end{array} \right]}_{\mathcal{D}} \left[ \begin{array}{c} -{\phi^{(1)}_{1}} {{\boldsymbol{\phi}}^{(1)}_{2}} \\ -2 C_{v} {\phi^{(1)}_{1}} {\phi^{(1)}_{3}} - {\bar{\varPhi}_{1} |{{\boldsymbol{\phi}}^{(1)}_{2}}|^{2}} \end{array} \right]. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} {O(1):} & \quad \bar{\varPhi}_1 = \bar{\varPsi}_1, \quad \bar{{\boldsymbol{\varPhi}}}_2 = \dfrac{\bar{{\boldsymbol{\varPsi}}}_2}{\bar{\varPsi}_1}, \quad \bar{{\boldsymbol{\varPhi}}}_3 = \dfrac{1}{C_v \bar{\varPsi}_1} \left( \bar{\varPsi}_3 - \dfrac{| \bar{{\boldsymbol{\varPsi}}}_2 |^2}{2 \bar{\varPsi}_1}\right),\\ {O(\epsilon):} & \quad \left[ \begin{array}{c} {\phi^{(1)}_{1}} \\ {{\boldsymbol{\phi}}^{(1)}_{2}} \\ \phi^{(1)}_{3} \end{array} \right] =\underbrace{\dfrac{1}{\bar{\varPhi}_{1}} \! \left[ \begin{array}{ccc} \bar{\varPhi}_{1} & 0 & 0 \\ -\bar{{\boldsymbol{\varPhi}}}_{2} & I & 0 \\ \dfrac{1}{2 C_{v}} \, | \bar{{\boldsymbol{\varPhi}}}_{2} |^2 - \bar{\varPhi}_{3} & -\dfrac{1}{C_{v}} \, \bar{{\boldsymbol{\varPhi}}}_{2}^T & \dfrac{1}{C_{v}} \end{array} \right]}_{\mathcal{C}} \left[ \begin{array}{c} {\psi^{(1)}_{1}} \\ {{\boldsymbol{\psi}}^{(1)}_{2}} \\ {\psi^{(1)}_{3}} \end{array} \right],\\ {O(\epsilon^2):} & \quad \left[ \begin{array}{c} {\phi^{(2)}_{1}} \\ {{\boldsymbol{\phi}}^{(2)}_{2}} \\ \phi^{(2)}_{3} \end{array} \right] = \mathcal{C} \left[ \begin{array}{c} {\psi^{(2)}_{1}} \\ {{\boldsymbol{\psi}}^{(2)}_{2}} \\ \psi^{(2)}_{3} \end{array} \right] + \underbrace{\dfrac{1}{\bar{\varPhi}_{1}} \! \left[ \begin{array}{cc} 0 & 0 \\ I & 0 \\ 0 & \dfrac{1}{2 C_{v}} \end{array} \right]}_{\mathcal{D}} \left[ \begin{array}{c} -{\phi^{(1)}_{1}} {{\boldsymbol{\phi}}^{(1)}_{2}} \\ -2 C_{v} {\phi^{(1)}_{1}} {\phi^{(1)}_{3}} - {\bar{\varPhi}_{1} |{{\boldsymbol{\phi}}^{(1)}_{2}}|^{2}} \end{array} \right]. \end{aligned} \right\} \end{equation}Appendix C. Energy transport equation in streamline coordinates
The terms on the right-hand side of transport equation (3.17) for streamwise specific kinetic energy ![]() $\mathcal {E}_s \mathrel {\mathop :}= u_s^{\prime } u_s^{\prime }$ are determined by
$\mathcal {E}_s \mathrel {\mathop :}= u_s^{\prime } u_s^{\prime }$ are determined by
 \begin{equation} \left. \begin{aligned} \text{Production:}\ \mathcal{P} & \, \mathrel{\mathop:}= \, -{u^\prime_{s} u^\prime_{n}} \partial_{n} \bar{u}_{s} - {u^\prime_{s} u^\prime_{s}} \partial_{s} \bar{u}_{s} - {\rho^{\prime} u_{s}^{\prime}} \dfrac{\bar{u}_{s}}{{\bar{\rho}}} \partial_{s} \bar{u}_{s},\\ \text{Source:}\ \mathcal{S} & \, \mathrel{\mathop:}= \, -\frac{u^\prime_{s}}{\bar{\rho}} {\partial_s} p^{\prime},\\ \text{Viscous:}\ \mathcal{V} & \, \mathrel{\mathop:}= \, \frac{\bar{\mu}}{\bar{\rho}}\left( 2u^\prime_{s} \partial_{s} u^\prime_{s} + u^\prime_{s} \partial_{n} \left( \partial_{n} u^\prime_{s} + \partial_{s} u^\prime_{n} \right) + \partial_{z} u^\prime_{s} \left( \partial_s w^\prime + \partial_{z} u^\prime_s \right) \right),\\ \text{Curvature:}\ \mathcal{K} & \, \mathrel{\mathop:}= \, -K_{c} u^\prime_{s} u^\prime_{n} - \frac{2\bar{\mu}}{\bar{\rho}\bar{u}^2_{s}}\left(K^2_{s} u^\prime_{s} u^\prime_{n} + K^2_{c} u^\prime_{s} u^\prime_{s}\right)\\ & \quad+ \, \phantom{\mathrel{\mathop:}=} \, \frac{1}{{\bar{\rho}}}\left(u^\prime_{s} \partial_{s} \left(\frac{2\bar{\mu}K_{c} u^\prime_{n}}{\bar{u}_{s}} \right) - u^\prime_{s} \partial_n \left( \frac{\bar{\mu} (K_c u^\prime_s + K_s u^\prime_n)}{\bar{u}_{s}} \right) \right) \\ & \quad+ \, \phantom{\mathrel{\mathop:}=} \, \frac{2\bar{\mu}}{\bar{u}_{s} \bar{\rho}} \left( K_s u^\prime_{s} \partial_{s} u^\prime_{s} + K_c u^\prime_{s} \left({\partial_n} u^\prime_{s} + {\partial_s} u^\prime_{n} \right) - K_s u^\prime_{s} {\partial_n} u^\prime_{n} \right). \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \text{Production:}\ \mathcal{P} & \, \mathrel{\mathop:}= \, -{u^\prime_{s} u^\prime_{n}} \partial_{n} \bar{u}_{s} - {u^\prime_{s} u^\prime_{s}} \partial_{s} \bar{u}_{s} - {\rho^{\prime} u_{s}^{\prime}} \dfrac{\bar{u}_{s}}{{\bar{\rho}}} \partial_{s} \bar{u}_{s},\\ \text{Source:}\ \mathcal{S} & \, \mathrel{\mathop:}= \, -\frac{u^\prime_{s}}{\bar{\rho}} {\partial_s} p^{\prime},\\ \text{Viscous:}\ \mathcal{V} & \, \mathrel{\mathop:}= \, \frac{\bar{\mu}}{\bar{\rho}}\left( 2u^\prime_{s} \partial_{s} u^\prime_{s} + u^\prime_{s} \partial_{n} \left( \partial_{n} u^\prime_{s} + \partial_{s} u^\prime_{n} \right) + \partial_{z} u^\prime_{s} \left( \partial_s w^\prime + \partial_{z} u^\prime_s \right) \right),\\ \text{Curvature:}\ \mathcal{K} & \, \mathrel{\mathop:}= \, -K_{c} u^\prime_{s} u^\prime_{n} - \frac{2\bar{\mu}}{\bar{\rho}\bar{u}^2_{s}}\left(K^2_{s} u^\prime_{s} u^\prime_{n} + K^2_{c} u^\prime_{s} u^\prime_{s}\right)\\ & \quad+ \, \phantom{\mathrel{\mathop:}=} \, \frac{1}{{\bar{\rho}}}\left(u^\prime_{s} \partial_{s} \left(\frac{2\bar{\mu}K_{c} u^\prime_{n}}{\bar{u}_{s}} \right) - u^\prime_{s} \partial_n \left( \frac{\bar{\mu} (K_c u^\prime_s + K_s u^\prime_n)}{\bar{u}_{s}} \right) \right) \\ & \quad+ \, \phantom{\mathrel{\mathop:}=} \, \frac{2\bar{\mu}}{\bar{u}_{s} \bar{\rho}} \left( K_s u^\prime_{s} \partial_{s} u^\prime_{s} + K_c u^\prime_{s} \left({\partial_n} u^\prime_{s} + {\partial_s} u^\prime_{n} \right) - K_s u^\prime_{s} {\partial_n} u^\prime_{n} \right). \end{aligned} \right\} \end{equation}
Here, ![]() $K_{c}$ and
$K_{c}$ and ![]() $K_{s}$ denote contributions that arise from the curvature normal to the streamlines and from deceleration along the streamline direction, respectively, and
$K_{s}$ denote contributions that arise from the curvature normal to the streamlines and from deceleration along the streamline direction, respectively, and ![]() $\bar {\mu }$ is the coefficient of viscosity associated with the laminar base flow. The curvature terms
$\bar {\mu }$ is the coefficient of viscosity associated with the laminar base flow. The curvature terms ![]() $K_{c}$ and
$K_{c}$ and ![]() $K_{s}$ result from transformation into a streamline coordinate system (Yousefi & Veron Reference Yousefi and Veron2020) and they can be analytically expressed using the mean vorticity and the velocity gradients of the laminar 2-D base flow (Finnigan Reference Finnigan1983); see (3.19b).
$K_{s}$ result from transformation into a streamline coordinate system (Yousefi & Veron Reference Yousefi and Veron2020) and they can be analytically expressed using the mean vorticity and the velocity gradients of the laminar 2-D base flow (Finnigan Reference Finnigan1983); see (3.19b).
Appendix D. Transport equation for the fluctuation shear stress
The transport equation that governs the evolution of time and spanwise-averaged fluctuation shear stress ![]() ${R}_{sn}\mathrel {\mathop :}= \langle {u^\prime _{s}u^\prime _{n}}\rangle$ in
${R}_{sn}\mathrel {\mathop :}= \langle {u^\prime _{s}u^\prime _{n}}\rangle$ in ![]() $(s,n,z)$ coordinates is given by
$(s,n,z)$ coordinates is given by
The viscous terms are neglected because they do not contribute to the transport of ![]() $R_{sn}$ and the terms on the right-hand side are determined by
$R_{sn}$ and the terms on the right-hand side are determined by
 \begin{equation} \left. \begin{aligned} \text{Production:}\ \mathcal{P}_{r} & \, \mathrel{\mathop:}={-} {R}_{s n} \partial_s \bar{u}_{s} \,-\, \langle{u^\prime_{n}u^\prime_{n}\rangle} \partial_n \bar{u}_{s} + \langle{\rho^{\prime} u^\prime_{s}\rangle} \frac{\partial_{n} \bar{p}}{\bar{\rho}^2} + \langle{\rho^{\prime} u^\prime_{n}\rangle} \frac{\partial_{s} \bar{p}}{\bar{\rho}^2},\\ \text{Source:}\ \mathcal{S}_{r} & \, \mathrel{\mathop:}=\, -\frac{1}{\bar{\rho}} \, ({\langle{u^\prime_{n}{\partial_s} p^{\prime}}\rangle} +{\langle{u^\prime_{s}{\partial_n} p^{\prime}}}\rangle ),\\ \text{Curvature:}\ \mathcal{K}_{r} & \, \mathrel{\mathop:}=\, \left( 2E_{s} - \langle{u^\prime_{n}u^\prime_{n}}\rangle\right) K_{c} - {R}_{s n} K_{s}. \end{aligned} \right\} \end{equation}
\begin{equation} \left. \begin{aligned} \text{Production:}\ \mathcal{P}_{r} & \, \mathrel{\mathop:}={-} {R}_{s n} \partial_s \bar{u}_{s} \,-\, \langle{u^\prime_{n}u^\prime_{n}\rangle} \partial_n \bar{u}_{s} + \langle{\rho^{\prime} u^\prime_{s}\rangle} \frac{\partial_{n} \bar{p}}{\bar{\rho}^2} + \langle{\rho^{\prime} u^\prime_{n}\rangle} \frac{\partial_{s} \bar{p}}{\bar{\rho}^2},\\ \text{Source:}\ \mathcal{S}_{r} & \, \mathrel{\mathop:}=\, -\frac{1}{\bar{\rho}} \, ({\langle{u^\prime_{n}{\partial_s} p^{\prime}}\rangle} +{\langle{u^\prime_{s}{\partial_n} p^{\prime}}}\rangle ),\\ \text{Curvature:}\ \mathcal{K}_{r} & \, \mathrel{\mathop:}=\, \left( 2E_{s} - \langle{u^\prime_{n}u^\prime_{n}}\rangle\right) K_{c} - {R}_{s n} K_{s}. \end{aligned} \right\} \end{equation}Appendix E. Grid convergence for DNS
Figure 25 plots the energy of the streaks at ![]() $(\omega,\lambda _{z}) = (0,1.5)$ generated by the interaction of oblique waves with
$(\omega,\lambda _{z}) = (0,1.5)$ generated by the interaction of oblique waves with ![]() $(\omega,\lambda _{z}) = (\pm 0.4, 3.0)$ in a computational domain with the following number of grid points: (G1)
$(\omega,\lambda _{z}) = (\pm 0.4, 3.0)$ in a computational domain with the following number of grid points: (G1) ![]() $600 \times 249 \times 96$, (G2)
$600 \times 249 \times 96$, (G2) ![]() $900 \times 249 \times 192$ and (G3)
$900 \times 249 \times 192$ and (G3) ![]() $900 \times 249 \times 384$. The disturbance amplitude is set to
$900 \times 249 \times 384$. The disturbance amplitude is set to ![]() $a_{ob} = 2.50 \times 10^{2} A_{0}$. As shown in figure 25, the spatial evolution of the energy of the streaks is almost identical throughout the separation zone for all grids. All of our numerical computations in the paper are reported for (G3). In table 1 we also compare the resolution of (G3) with the discretization utilized in recent DNS studies of supersonic and hypersonic transitional and turbulent flows.
$a_{ob} = 2.50 \times 10^{2} A_{0}$. As shown in figure 25, the spatial evolution of the energy of the streaks is almost identical throughout the separation zone for all grids. All of our numerical computations in the paper are reported for (G3). In table 1 we also compare the resolution of (G3) with the discretization utilized in recent DNS studies of supersonic and hypersonic transitional and turbulent flows.

Figure 25. Comparison of the energy of the streaks at ![]() $\lambda _{z} = 1.5$ for three different grid resolutions.
$\lambda _{z} = 1.5$ for three different grid resolutions.
Table 1. Summary of DNS computations of transition and turbulence reported in (1) Duan et al. (Reference Duan, Beekman and Martín2011), (2) Mayer et al. (Reference Mayer, Von Terzi and Fasel2011), (3) Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011), (4) Franko & Lele (Reference Franko and Lele2013).

Appendix F. Distribution of wall temperature
In addition to the skin friction, the distribution of wall temperature provides insights into the thermal effects encountered in compressible boundary layer flows along the transition zone. In flows with adiabatic walls there is no heat transfer to the wall and viscous dissipation near the wall converts kinetic into internal energy. This leads to high temperatures near the wall as well as in the associated thermal boundary layer and 3-D patterns in the wall temperature are caused by temperature transport within the boundary layer by flow fluctuations.
Figure 26(a,b) illustrates instantaneous and mean wall temperatures in the transition zone. In contrast to the instantaneous skin friction, where the streaks determine the spanwise modulation prior to flow transition, the instantaneous wall temperature contains strong imprints of unsteady oblique waves. The role of the streaks and higher spanwise harmonics becomes apparent when we examine the time-averaged wall temperature.

Figure 26. Streamwise variations of (a) instantaneous, (b) time-averaged, and (c) time- and spanwise-averaged wall temperatures.
In figure 26(c) we illustrate the mean wall temperature along the double wedge. Even though temperature variations are not significant under present conditions, its analysis can be informative for different free-stream conditions. Comparison with the double-wedge laminar solution shows that the wall temperature is higher in the 3-D flow field immediately after the separation point and that it rises rapidly post-reattachment. In the transition zone we observe an overshoot before reduction to its turbulent value.