Article contents
Numerical study of flow-induced vibration of a circular cylinder with attached flexible splitter plate at low 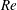 $Re$
$Re$
Published online by Cambridge University Press: 10 October 2019
Abstract
Flow-induced vibration (FIV) of an elastically mounted circular cylinder with an attached splitter plate in uniform flow is studied numerically via a stabilized space–time finite element method. The Reynolds number based on the cylinder diameter 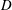 $D$ and the free-stream speed is restricted to 150. The ratio of the density of the body to that of the fluid, for the major part of the study, is 10. Two different reduced speeds are defined to quantify the compliance of the elastic support and flexibility of the splitter plate, respectively:
$D$ and the free-stream speed is restricted to 150. The ratio of the density of the body to that of the fluid, for the major part of the study, is 10. Two different reduced speeds are defined to quantify the compliance of the elastic support and flexibility of the splitter plate, respectively: 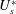 $U_{s}^{\ast }$ based on the natural frequency of the spring–mass system and
$U_{s}^{\ast }$ based on the natural frequency of the spring–mass system and 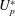 $U_{p}^{\ast }$ based on the fundamental natural frequency of the plate. Flow past a stationary cylinder (
$U_{p}^{\ast }$ based on the fundamental natural frequency of the plate. Flow past a stationary cylinder (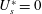 $U_{s}^{\ast }=0$) with a flexible splitter plate of length
$U_{s}^{\ast }=0$) with a flexible splitter plate of length 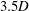 $3.5D$ is studied at different values of
$3.5D$ is studied at different values of 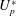 $U_{p}^{\ast }$. The vibration response of the plate exhibits lock-in with various eigenmodes of the plate in different ranges of
$U_{p}^{\ast }$. The vibration response of the plate exhibits lock-in with various eigenmodes of the plate in different ranges of 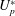 $U_{p}^{\ast }$. The onsets of these lock-in regions are abrupt and hysteretic. The elastically mounted cylinder, without the splitter plate, undergoes large-amplitude vortex-induced vibration (VIV) for
$U_{p}^{\ast }$. The onsets of these lock-in regions are abrupt and hysteretic. The elastically mounted cylinder, without the splitter plate, undergoes large-amplitude vortex-induced vibration (VIV) for 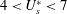 $4<U_{s}^{\ast }<7$. These large-amplitude oscillations are a consequence of synchronization, wherein the vortex shedding frequency locks in to the cylinder oscillation frequency. A rigid splitter plate attached to the cylinder reduces significantly the peak amplitude during VIV. Increasing the length of the plate from
$4<U_{s}^{\ast }<7$. These large-amplitude oscillations are a consequence of synchronization, wherein the vortex shedding frequency locks in to the cylinder oscillation frequency. A rigid splitter plate attached to the cylinder reduces significantly the peak amplitude during VIV. Increasing the length of the plate from 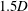 $1.5D$ to
$1.5D$ to 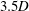 $3.5D$ only marginally affects the peak amplitude. It, however, leads to a wider range of lock-in. Unlike the case of an isolated cylinder, the lock-in and desynchronization regimes are not well demarcated in the presence of the splitter plate. Further, galloping is observed beyond a critical value of
$3.5D$ only marginally affects the peak amplitude. It, however, leads to a wider range of lock-in. Unlike the case of an isolated cylinder, the lock-in and desynchronization regimes are not well demarcated in the presence of the splitter plate. Further, galloping is observed beyond a critical value of 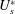 $U_{s}^{\ast }$; the amplitude of vibration increases with an increase in
$U_{s}^{\ast }$; the amplitude of vibration increases with an increase in 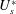 $U_{s}^{\ast }$ while the vibration frequency is relatively low and remains nearly constant. Increase in plate length delays, in terms of
$U_{s}^{\ast }$ while the vibration frequency is relatively low and remains nearly constant. Increase in plate length delays, in terms of 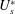 $U_{s}^{\ast }$, the onset of galloping. It is also found that the flexibility of the plate affects the maximum oscillation amplitude in the VIV regime. It also dictates the presence/absence of galloping. The system behaves similar to an isolated cylinder for a very flexible plate. The response is devoid of galloping, but relatively large amplitude of oscillation is observed during lock-in. The behaviour of the cylinder with a stiff plate is similar to that with the rigid one. The galloping instability sets in when the flexibility of the plate is less than a certain value (
$U_{s}^{\ast }$, the onset of galloping. It is also found that the flexibility of the plate affects the maximum oscillation amplitude in the VIV regime. It also dictates the presence/absence of galloping. The system behaves similar to an isolated cylinder for a very flexible plate. The response is devoid of galloping, but relatively large amplitude of oscillation is observed during lock-in. The behaviour of the cylinder with a stiff plate is similar to that with the rigid one. The galloping instability sets in when the flexibility of the plate is less than a certain value (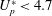 $U_{p}^{\ast }<4.7$, approximately for
$U_{p}^{\ast }<4.7$, approximately for 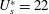 $U_{s}^{\ast }=22$). The VIV and galloping are separated by a range of
$U_{s}^{\ast }=22$). The VIV and galloping are separated by a range of 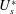 $U_{s}^{\ast }$ in which the flow is either steady, for longer plates, or exhibits very weak vortex shedding. In the VIV regime, the plate tip and cylinder vibrate in phase for low
$U_{s}^{\ast }$ in which the flow is either steady, for longer plates, or exhibits very weak vortex shedding. In the VIV regime, the plate tip and cylinder vibrate in phase for low 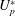 $U_{p}^{\ast }$; their motion is out of phase for larger
$U_{p}^{\ast }$; their motion is out of phase for larger 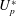 $U_{p}^{\ast }$. The change in phase is also associated with change in the frequency of vibration. At low
$U_{p}^{\ast }$. The change in phase is also associated with change in the frequency of vibration. At low 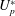 $U_{p}^{\ast }$, the frequency of vibration is close to the first natural frequency of the system, while at high
$U_{p}^{\ast }$, the frequency of vibration is close to the first natural frequency of the system, while at high 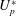 $U_{p}^{\ast }$ it becomes closer to the second natural frequency. The vibration amplitude of the cylinder is close to maximum in the VIV regime for
$U_{p}^{\ast }$ it becomes closer to the second natural frequency. The vibration amplitude of the cylinder is close to maximum in the VIV regime for 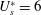 $U_{s}^{\ast }=6$. Computations for various
$U_{s}^{\ast }=6$. Computations for various 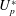 $U_{p}^{\ast }$, for
$U_{p}^{\ast }$, for 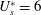 $U_{s}^{\ast }=6$ and
$U_{s}^{\ast }=6$ and 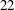 $22$, are utilized to determine optimal flexibility that leads to minimal FIV. The effect of the length of the flexible splitter plate, mass ratio and damping ratio is studied. A strategy is proposed to utilize the computations from various combinations of
$22$, are utilized to determine optimal flexibility that leads to minimal FIV. The effect of the length of the flexible splitter plate, mass ratio and damping ratio is studied. A strategy is proposed to utilize the computations from various combinations of 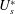 $U_{s}^{\ast }$ and
$U_{s}^{\ast }$ and 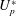 $U_{p}^{\ast }$ to choose the appropriate flexibility of the attached splitter plate to minimize FIV.
$U_{p}^{\ast }$ to choose the appropriate flexibility of the attached splitter plate to minimize FIV.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 57
- Cited by

