Article contents
Numerical study of bluntness effects on laminar leading edge separation in hypersonic flow
Published online by Cambridge University Press: 13 September 2019
Abstract
Bluntness effects on laminar hypersonic leading edge separation are investigated numerically at Mach number 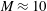 $M\approx 10$, unit Reynolds number
$M\approx 10$, unit Reynolds number 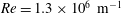 $Re=1.3\times 10^{6}~\text{m}^{-1}$, specific enthalpy
$Re=1.3\times 10^{6}~\text{m}^{-1}$, specific enthalpy 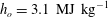 $h_{o}=3.1~\text{MJ}~\text{kg}^{-1}$ and wall-to-stagnation temperature ratio
$h_{o}=3.1~\text{MJ}~\text{kg}^{-1}$ and wall-to-stagnation temperature ratio 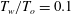 $T_{w}/T_{o}=0.1$. Such effects are important from an experimental point of view and because bluntness can affect a separated flow favourably or adversely. In this study, two blunt leading edge cases of small radius (
$T_{w}/T_{o}=0.1$. Such effects are important from an experimental point of view and because bluntness can affect a separated flow favourably or adversely. In this study, two blunt leading edge cases of small radius (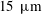 $15~\unicode[STIX]{x03BC}\text{m}$) and large radius (
$15~\unicode[STIX]{x03BC}\text{m}$) and large radius (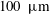 $100~\unicode[STIX]{x03BC}\text{m}$) are investigated. A comparison with the idealised sharp leading edge case is also given. General flow features and surface parameters such as the shear stress, pressure and heat flux are presented and analysed. The results have also been interpreted in terms of Cheng’s displacement-bluntness similitude parameter affecting the size of separation. Previous experiments by Holden delineated small and large bluntness effects based on Cheng’s parameter and considering small to moderate separated regions. In this study, leading edge separation was found to suppress the favourable effect of bluntness in delaying separation. Bluntness, furthermore, seemed to promote the appearance of secondary vortices within a main separated region. Analysis of reverse flow boundary layer profiles such as velocity, pressure and temperature is also given. It is shown that bluntness accentuates large transverse gradients. This in turn adversely effects the reverse flow boundary layer leading to the appearance of secondary vortices.
$100~\unicode[STIX]{x03BC}\text{m}$) are investigated. A comparison with the idealised sharp leading edge case is also given. General flow features and surface parameters such as the shear stress, pressure and heat flux are presented and analysed. The results have also been interpreted in terms of Cheng’s displacement-bluntness similitude parameter affecting the size of separation. Previous experiments by Holden delineated small and large bluntness effects based on Cheng’s parameter and considering small to moderate separated regions. In this study, leading edge separation was found to suppress the favourable effect of bluntness in delaying separation. Bluntness, furthermore, seemed to promote the appearance of secondary vortices within a main separated region. Analysis of reverse flow boundary layer profiles such as velocity, pressure and temperature is also given. It is shown that bluntness accentuates large transverse gradients. This in turn adversely effects the reverse flow boundary layer leading to the appearance of secondary vortices.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 8
- Cited by

