Article contents
Numerical investigation on body-wake flow interaction over rod–airfoil configuration
Published online by Cambridge University Press: 14 August 2015
Abstract
Numerical investigations of body-wake interactions were carried out by simulating the flow over a rod–airfoil configuration using high-order implicit large eddy simulation (HILES) for the incoming velocity 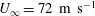 $U_{\infty }=72~\text{m}~\text{s}^{-1}$ and a Reynolds number based on the airfoil chord
$U_{\infty }=72~\text{m}~\text{s}^{-1}$ and a Reynolds number based on the airfoil chord 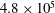 $4.8\times 10^{5}$ . The flow over five different rod–airfoil configurations with different distances of
$4.8\times 10^{5}$ . The flow over five different rod–airfoil configurations with different distances of 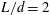 $L/d=2$ , 4, 6, 8 and 10, respectively, were calculated for the analysis of body-wake interaction phenomena. Various fundamental mechanisms dictating the intricate flow phenomena including force varying regulation, flow structures and flow patterns in the interaction region, turbulent fluctuations and their suppression, noise radiation and fluid resonant oscillation, have been studied systematically. Due to the airfoil downstream, a relatively higher base pressure is exerted on the surface of the cylinder upstream, and the pressure fluctuation on the surface of the rod–airfoil configuration with
$L/d=2$ , 4, 6, 8 and 10, respectively, were calculated for the analysis of body-wake interaction phenomena. Various fundamental mechanisms dictating the intricate flow phenomena including force varying regulation, flow structures and flow patterns in the interaction region, turbulent fluctuations and their suppression, noise radiation and fluid resonant oscillation, have been studied systematically. Due to the airfoil downstream, a relatively higher base pressure is exerted on the surface of the cylinder upstream, and the pressure fluctuation on the surface of the rod–airfoil configuration with  $L/d=2$ is significantly suppressed, resulting in a reduction of the fluctuating lift. Following the distance between the cylinder and airfoil strongly decreases, Kármán-street shedding is suppressed due to the blocking effect. The flow in this interaction region has two opposite tendencies: the influence of the airfoil on the steady flow is to accelerate it and the counter-rotating vortices connecting with the leading edge of the airfoil tend to slow the flow down. There may be two flow patterns associated with the interference region, i.e. the Kármán-street suppressing mode and the Kármán-street shedding mode. The primary vortex shedding behind the cylinder upstream, and the shedding wake impingement onto the airfoil downstream, play a dominant role in the production of turbulent fluctuations. When primary vortex shedding is suppressed, the intensity of impingement is weakened, resulting in a significant suppression of the turbulent fluctuations. Due to these factors, a special broadband noise without a manifestly distinguishable peak is radiated by the rod–airfoil configuration with
$L/d=2$ is significantly suppressed, resulting in a reduction of the fluctuating lift. Following the distance between the cylinder and airfoil strongly decreases, Kármán-street shedding is suppressed due to the blocking effect. The flow in this interaction region has two opposite tendencies: the influence of the airfoil on the steady flow is to accelerate it and the counter-rotating vortices connecting with the leading edge of the airfoil tend to slow the flow down. There may be two flow patterns associated with the interference region, i.e. the Kármán-street suppressing mode and the Kármán-street shedding mode. The primary vortex shedding behind the cylinder upstream, and the shedding wake impingement onto the airfoil downstream, play a dominant role in the production of turbulent fluctuations. When primary vortex shedding is suppressed, the intensity of impingement is weakened, resulting in a significant suppression of the turbulent fluctuations. Due to these factors, a special broadband noise without a manifestly distinguishable peak is radiated by the rod–airfoil configuration with  $L/d=2$ . The fluid resonant oscillation within the flow interaction between the turbulent wake and the bodies was further investigated by adopting a feedback model, which confirmed that the effect of fluid resonant oscillation becomes stronger when
$L/d=2$ . The fluid resonant oscillation within the flow interaction between the turbulent wake and the bodies was further investigated by adopting a feedback model, which confirmed that the effect of fluid resonant oscillation becomes stronger when 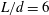 $L/d=6$ and 10. The results obtained in this study provide physical insight into the understanding of the mechanisms relevant to the body-wake interaction.
$L/d=6$ and 10. The results obtained in this study provide physical insight into the understanding of the mechanisms relevant to the body-wake interaction.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 62
- Cited by


