Article contents
Numerical investigation of wake flow regimes behind a high-speed rotating circular cylinder in steady flow
Published online by Cambridge University Press: 18 September 2019
Abstract
Flow around a high-speed rotating circular cylinder for 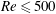 $Re\leqslant 500$ is investigated numerically. The Reynolds number is defined as
$Re\leqslant 500$ is investigated numerically. The Reynolds number is defined as 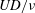 $UD/\unicode[STIX]{x1D708}$ with
$UD/\unicode[STIX]{x1D708}$ with 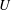 $U$,
$U$, 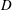 $D$ and
$D$ and  $\unicode[STIX]{x1D708}$ being the free-stream flow velocity, the diameter of the cylinder and the kinematic viscosity of the fluid, respectively. The aim of this study is to investigate the effect of a high rotation rate on the wake flow for a range of Reynolds numbers. Simulations are performed for Reynolds numbers of 100, 150, 200, 250 and 500 and a wide range of rotation rates from 1.6 to 6 with an increment of 0.2. Rotation rate is the ratio of the rotational speed of the cylinder surface to the incoming fluid velocity. A systematic study is performed to investigate the effect of rotation rate on the flow transition to different flow regimes. It is found that there is a transition from a two-dimensional vortex shedding mode to no vortex shedding mode when the rotation rate is increased beyond a critical value for Reynolds numbers between 100 and 200. Further increase in rotation rate results in a transition to three-dimensional flow which is characterized by the presence of finger-shaped (FV) vortices that elongate in the wake of the cylinder and very weak ring-shaped vortices (RV) that wrap the surface of the cylinder. The no vortex shedding mode is not observed at Reynolds numbers greater than or equal to 250 since the flow remains three-dimensional. As the rotation rate is increased further, the occurrence frequency and size of the ring-shaped vortices increases and the flow is dominated by RVs. The RVs become bigger in size and the flow becomes chaotic with increasing rotation rate. A detailed analysis of the flow structures shows that the vortices always exist in pairs and the strength of separated shear layers increases with the increase of rotation rate. A map of flow regimes on a plane of Reynolds number and rotation rate is presented.
$\unicode[STIX]{x1D708}$ being the free-stream flow velocity, the diameter of the cylinder and the kinematic viscosity of the fluid, respectively. The aim of this study is to investigate the effect of a high rotation rate on the wake flow for a range of Reynolds numbers. Simulations are performed for Reynolds numbers of 100, 150, 200, 250 and 500 and a wide range of rotation rates from 1.6 to 6 with an increment of 0.2. Rotation rate is the ratio of the rotational speed of the cylinder surface to the incoming fluid velocity. A systematic study is performed to investigate the effect of rotation rate on the flow transition to different flow regimes. It is found that there is a transition from a two-dimensional vortex shedding mode to no vortex shedding mode when the rotation rate is increased beyond a critical value for Reynolds numbers between 100 and 200. Further increase in rotation rate results in a transition to three-dimensional flow which is characterized by the presence of finger-shaped (FV) vortices that elongate in the wake of the cylinder and very weak ring-shaped vortices (RV) that wrap the surface of the cylinder. The no vortex shedding mode is not observed at Reynolds numbers greater than or equal to 250 since the flow remains three-dimensional. As the rotation rate is increased further, the occurrence frequency and size of the ring-shaped vortices increases and the flow is dominated by RVs. The RVs become bigger in size and the flow becomes chaotic with increasing rotation rate. A detailed analysis of the flow structures shows that the vortices always exist in pairs and the strength of separated shear layers increases with the increase of rotation rate. A map of flow regimes on a plane of Reynolds number and rotation rate is presented.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 18
- Cited by

