Article contents
Numerical calculations of two-dimensional large Prandtl number convection in a box
Published online by Cambridge University Press: 24 July 2013
Abstract
Convection from an isolated heat source in a chamber has been previously studied numerically, experimentally and analytically. These have not covered long time spans for wide ranges of Rayleigh number Ra and Prandtl number Pr. Numerical calculations of constant viscosity convection partially fill the gap in the ranges 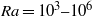 $\mathit{Ra}= 1{0}^{3} {{\unicode{x2013}}}1{0}^{6} $ and
$\mathit{Ra}= 1{0}^{3} {{\unicode{x2013}}}1{0}^{6} $ and 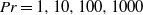 $\mathit{Pr}= 1, 10, 100, 1000$ and
$\mathit{Pr}= 1, 10, 100, 1000$ and 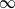 $\infty $ . Calculations begin with cold fluid everywhere and localized hot temperature at the centre of the bottom of a square two-dimensional chamber. For
$\infty $ . Calculations begin with cold fluid everywhere and localized hot temperature at the centre of the bottom of a square two-dimensional chamber. For 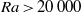 $\mathit{Ra}\gt 20\hspace{0.167em} 000$ , temperature increases above the hot bottom and forms a rising plume head. The head has small internal recirculation and minor outward conduction of heat during ascent. The head approaches the top, flattens, splits and the two remnants are swept to the sidewalls and diffused away. The maximum velocity and the top centre heat flux climb to maxima during head ascent and then adjust toward constant values. Two steady cells are separated by a vertical thermal conduit. This sequence is followed for every value of
$\mathit{Ra}\gt 20\hspace{0.167em} 000$ , temperature increases above the hot bottom and forms a rising plume head. The head has small internal recirculation and minor outward conduction of heat during ascent. The head approaches the top, flattens, splits and the two remnants are swept to the sidewalls and diffused away. The maximum velocity and the top centre heat flux climb to maxima during head ascent and then adjust toward constant values. Two steady cells are separated by a vertical thermal conduit. This sequence is followed for every value of 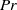 $Pr$ number, although lower Pr convection lags in time. For
$Pr$ number, although lower Pr convection lags in time. For 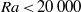 $\mathit{Ra}\lt 20\hspace{0.167em} 000$ there is no plume head, and no streamfunction and heat flux maxima with time. For sufficiently large Ra and all values of Pr, an oscillation develops at roughly
$\mathit{Ra}\lt 20\hspace{0.167em} 000$ there is no plume head, and no streamfunction and heat flux maxima with time. For sufficiently large Ra and all values of Pr, an oscillation develops at roughly 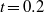 $t= 0. 2$ , with the two cells alternately strengthening and weakening. This changes to a steady flow with two unequal cells that at roughly
$t= 0. 2$ , with the two cells alternately strengthening and weakening. This changes to a steady flow with two unequal cells that at roughly 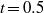 $t= 0. 5$ develops a second oscillation.
$t= 0. 5$ develops a second oscillation.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 12
- Cited by

