Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-16T21:17:51.543Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal stress differences, their origin and constitutive relations for a sheared granular fluid

Published online by Cambridge University Press:  19 April 2016

Saikat Saha  and
Meheboob Alam
Saikat Saha
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: meheboob@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The rheology of the steady uniform shear flow of smooth inelastic spheres is analysed by choosing the anisotropic/triaxial Gaussian as the single-particle distribution function. An exact solution of the balance equation for the second-moment tensor of velocity fluctuations, truncated at the ‘Burnett order’ (second order in the shear rate), is derived, leading to analytical expressions for the first and second (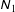$\unicode[STIX]{x1D615}_{1}$ and $\unicode[STIX]{x1D615}_{2}$) normal stress differences and other transport coefficients as functions of density (i.e. the volume fraction of particles), restitution coefficient and other control parameters. Moreover, the perturbation solution at fourth order in the shear rate is obtained which helped to assess the range of validity of Burnett-order constitutive relations. Theoretical expressions for both 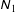$\unicode[STIX]{x1D615}_{1}$ and 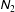$\unicode[STIX]{x1D615}_{2}$ and those for pressure and shear viscosity agree well with particle simulation data for the uniform shear flow of inelastic hard spheres for a large range of volume fractions spanning from the dilute regime to close to the freezing-point density (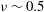${\it\nu}\sim 0.5$). While the first normal stress difference 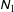$\unicode[STIX]{x1D615}_{1}$ is found to be positive in the dilute limit and decreases monotonically to zero in the dense limit, the second normal stress difference $\unicode[STIX]{x1D615}_{2}$ is negative and positive in the dilute and dense limits, respectively, and undergoes a sign change at a finite density due to the sign change of its kinetic component. It is shown that the origin of 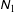$\unicode[STIX]{x1D615}_{1}$ is tied to the non-coaxiality (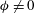${\it\phi}\neq 0$) between the eigendirections of the second-moment tensor 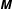$\unicode[STIX]{x1D648}$ and those of the shear tensor 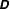$\unicode[STIX]{x1D63F}$. In contrast, the origin of 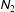$\unicode[STIX]{x1D615}_{2}$ in the dilute limit is tied to the ‘excess’ temperature (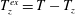$T_{z}^{ex}=T-T_{z}$, where 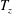$T_{z}$ and 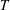$T$ are the $z$-component and the average of the granular temperature, respectively) along the mean vorticity ($z$) direction, whereas its origin in the dense limit is tied to the imposed shear field.

JFM classification

Complex Fluids: Complex Fluids Granular media: Granular media Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 549 - 580
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alam, M. & Chikkadi, V. K. 2010 Velocity distribution function and correlations in a granular Poiseuille flow. J. Fluid Mech. 653, 175–219.Google Scholar
Alam, M. & Luding, S. 2003a First normal stress difference and crystallization in sheared granular fluid. Phys. Fluids 15, 2298–2312.Google Scholar
Alam, M. & Luding, S. 2003b Rheology of bidisperse granular mixtures via event-driven simulations. J. Fluid Mech. 476, 69–103.CrossRefGoogle Scholar
Alam, M. & Luding, S. 2005 Non-Newtonian granular fluid: simulation and theory. In Powders and Grains (ed. Garcia-Rojo, R., Herrmann, H. J. & McNamara, S.), pp. 1141–1144. A. A. Balkema.Google Scholar
Araki, S. 1988 The dynamics of particle disks: II. Effects of spin degrees of freedom. Icarus 76, 182–198.CrossRefGoogle Scholar
Araki, S. & Tremaine, S. 1986 The dynamics of dense particle disks. Icarus 65, 83–109.Google Scholar
Bagnold, R. A. 1954 Experiments on a gravity-free dispersion of large solid spheres in a newtonian fluid under shear. Proc. R. Soc. Lond. A 225, 49–63.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.CrossRefGoogle Scholar
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.CrossRefGoogle Scholar
Burnett, D. 1935 The distribution of velocities in a slightly non-uniform gas. Proc. Lond. Math. Soc. 39, 385–430.CrossRefGoogle Scholar
Campbell, C. S. 1989 The stress tensor for simple shear flows of a granular material. J. Fluid Mech. 203, 449–473.CrossRefGoogle Scholar
Carnahan, N. F. & Starling, K. E. 1969 Equation of state for non-attracting rigid spheres. J. Chem. Phys. 51, 635–636.CrossRefGoogle Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory for Non-uniform Gases. Cambridge University Press.Google Scholar
Chou, C. S. & Richman, M. W. 1998 Constitutive theory for homogeneous granular shear flows of highly inelastic spheres. Physica A 259, 430–448.Google Scholar
Couturier, E., Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 686, 26–39.Google Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.Google Scholar
Denn, M. M. & Morris, J. F. 2014 Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Engng 5, 203–228.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.Google Scholar
Garzo, V. & Dufty, J. W. 1999 Dense fluid transport for inelastic hard spheres. Phys. Rev. E 59, 5895–5911.Google ScholarPubMed
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.Google Scholar
Goldreich, P. & Tremaine, S. 1978 The velocity dispersion in Saturn’s rings. Icarus 34, 227–239.CrossRefGoogle Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Hatano, T. 2009 Growing length and time scales in a suspension of athermal particles. Phys. Rev. E 79, 050301.Google Scholar
Holway, L. H. 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9, 1658–1673.Google Scholar
Jaynes, E. T. 1957 Information theory and statistical mechanics. Phys. Rev. 106, 620–630.CrossRefGoogle Scholar
Jenkins, J. T. & Richman, M. W. 1985 Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.Google Scholar
Jenkins, J. T. & Richman, M. W. 1988 Plane simple shear of smooth inelastic circular disks. J. Fluid Mech. 192, 313–328.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441, 727–730.CrossRefGoogle ScholarPubMed
Kumar, N. & Luding, S. 2016 Memory of jamming – multiscale models for soft and granular matter. Granul. Matt. (in press).CrossRefGoogle Scholar
Lees, A. W. & Edwards, S. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 5, 1921–1929.Google Scholar
Lerner, E., Düring, G. & Wyart, M. 2012 A unified framework for non-Brownian suspension flows and soft amorphous solids. Proc. Natl Acad. Sci. USA 109, 4798–4803.Google Scholar
Lutsko, J. F. 2004 Rheology of dense polydisperse granular fluids under shear. Phys. Rev. E 70, 061101.Google ScholarPubMed
Lutsko, J. F. 2005 Transport properties of dense dissipative hard-sphere fluids for arbitrary energy loss models. Phys. Rev. E 72, 021306.Google Scholar
Mitarai, N. & Nakanishi, H. 2007 Velocity correlations in dense granular shear flows: effects on energy dissipation and normal stress. Phys. Rev. E 75, 031305.Google ScholarPubMed
Montanero, J. M., Garzo, V., Alam, M. & Luding, S. 2006 Rheology of two- and three-dimensional granular mixtures under uniform shear flow: Enskog kinetic theory versus molecular dynamics simulations. Granul. Matt. 8, 103–115.Google Scholar
Rao, K. K. & Nott, P. R. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Richman, M. W. 1989 The source of second moment in dilute granular flows of highly inelastic spheres. J. Rheol. 33, 1293–1306.Google Scholar
Rongali, R. & Alam, M. 2014 Higher-order effects on orientational correlation and relaxation dynamics in homogeneous cooling of a rough granular gas. Phys. Rev. E 89, 062201.Google Scholar
Saha, S. & Alam, M. 2014 Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method. J. Fluid Mech. 757, 251–296.Google Scholar
Santos, A., Garzo, V. & Dufty, J. W. 2004 Inherent rheology of a granular fluid in uniform shear. Phys. Rev. E 69, 061303.Google Scholar
Savage, S. B. & Jeffrey, D. J. 1981 The stress tensor in a granular flow at high shear rates. J. Fluid Mech. 110, 255–272.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.CrossRefGoogle Scholar
Singh, A. & Nott, P. R. 2003 Experimental measurements of the normal stresses in sheared Stokesian suspensions. J. Fluid Mech. 490, 293–320.Google Scholar
Suzuki, K. & Hayakawa, H. 2015 Divergence of viscosity in jammed granular materials: a theoretical approach. Phys. Rev. Lett. 115, 098001.Google Scholar
Torquato, S. 1995 Nearest-neighbour statistics for packings of hard spheres and disks. Inherent rheology of a granular fluid in uniform shear. Phys. Rev. E 51, 3170–3184.Google Scholar
Trulsson, M., Andreotti, B. & Claudin, P. 2012 Transition from the viscous to inertial regime in dense suspensions. Phys. Rev. Lett. 109, 118305.CrossRefGoogle ScholarPubMed
Walton, O. & Braun, R. L. 1986 Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. J. Rheol. 30, 949–965.Google Scholar
Supplementary material: PDF

Saha and Alam supplementary material

Saha and Alam supplementary material 1

Download Saha and Alam supplementary material(PDF)
PDF 166.2 KB