Article contents
Nonlinear interactions between an unstably stratified shear flow and a phase boundary
Published online by Cambridge University Press: 27 May 2021
Abstract
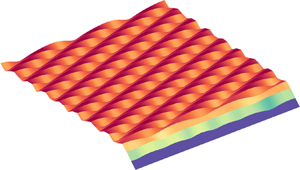
Well-resolved numerical simulations are used to study Rayleigh–Bénard–Poiseuille flow over an evolving phase boundary for moderate values of Péclet ( $Pe \in [0, 50]$) and Rayleigh (
$Pe \in [0, 50]$) and Rayleigh ( $Ra \in [2.15 \times 10^3, 10^6]$) numbers. The relative effects of mean shear and buoyancy are quantified using a bulk Richardson number:
$Ra \in [2.15 \times 10^3, 10^6]$) numbers. The relative effects of mean shear and buoyancy are quantified using a bulk Richardson number:  $Ri_b = Ra \cdot Pr/Pe^2 \in [8.6 \times 10^{-1}, 10^4]$, where
$Ri_b = Ra \cdot Pr/Pe^2 \in [8.6 \times 10^{-1}, 10^4]$, where  $Pr$ is the Prandtl number. For
$Pr$ is the Prandtl number. For  $Ri_b = O(1)$, we find that the Poiseuille flow inhibits convective motions, resulting in the heat transport being only due to conduction and, for
$Ri_b = O(1)$, we find that the Poiseuille flow inhibits convective motions, resulting in the heat transport being only due to conduction and, for  $Ri_b \gg 1$, the flow properties and heat transport closely correspond to the purely convective case. We also find that for certain
$Ri_b \gg 1$, the flow properties and heat transport closely correspond to the purely convective case. We also find that for certain  $Ra$ and
$Ra$ and  $Pe$, such that
$Pe$, such that  $Ri_b \in [15,95]$, there is a pattern competition for convection cells with a preferred aspect ratio. Furthermore, we find travelling waves at the solid–liquid interface when
$Ri_b \in [15,95]$, there is a pattern competition for convection cells with a preferred aspect ratio. Furthermore, we find travelling waves at the solid–liquid interface when  $Pe \neq ~0$, in qualitative agreement with other sheared convective flows in the experiments of Gilpin et al. (J. Fluid Mech., vol. 99(3), 1980, pp. 619–640) and the linear stability analysis of Toppaladoddi & Wettlaufer (J. Fluid Mech., vol. 868, 2019, pp. 648–665).
$Pe \neq ~0$, in qualitative agreement with other sheared convective flows in the experiments of Gilpin et al. (J. Fluid Mech., vol. 99(3), 1980, pp. 619–640) and the linear stability analysis of Toppaladoddi & Wettlaufer (J. Fluid Mech., vol. 868, 2019, pp. 648–665).
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 10
- Cited by


