Article contents
Nonlinear evolution of a baroclinic wave and imbalanced dissipation
Published online by Cambridge University Press: 09 September 2014
Abstract
We consider the nonlinear evolution of an unstable baroclinic wave in a regime of rotating stratified flow that is of relevance to interior circulation in the oceans and in the atmosphere: a regime characterized by small large-scale Rossby and Froude numbers, a small vertical to horizontal aspect ratio and no bounding horizontal surfaces. Using high-resolution simulations of the non-hydrostatic Boussinesq equations and companion integrations of the balanced quasi-geostrophic (QG) equations, we present evidence for a local route to dissipation of balanced energy directly through interior turbulent cascades. That is, analysis of simulations presented in this study suggest that a developing baroclinic instability can lead to secondary instabilities that can cascade a small fraction of the energy forward to unbalanced scales whereas the bulk of the energy is confined to large balanced scales. Mesoscale shear and strain resulting from the hydrostatic geostrophic baroclinic instability drive frontogenesis. The fronts in turn support ageostrophic secondary circulation and instabilities. These two processes acting together lead to a quick rise in dissipation rate which then reaches a peak and begins to fall slowly when frontogenesis slows down; eventually balanced and imbalanced modes decouple. A measurement of the dissipation of balanced energy by imbalanced processes reveals that it scales exponentially with Rossby number of the base flow. We expect that this scaling will hold more generally than for the specific set-up we consider given the fundamental nature of the dynamics involved. In other results, (a) a break is seen in the total energy (TE) spectrum at small scales: while a steep 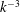 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k^{-3}$ geostrophic scaling (where
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k^{-3}$ geostrophic scaling (where 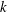 $k$ is the three-dimensional wavenumber) is seen at intermediate scales, the smaller scales display a shallower
$k$ is the three-dimensional wavenumber) is seen at intermediate scales, the smaller scales display a shallower 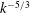 $k^{-5/3}$ scaling, reminiscent of the atmospheric spectra of Nastrom & Gage and (b) at the higher of the Rossby numbers considered a minimum is seen in the vertical shear spectrum, reminiscent of similar spectra obtained using in situ measurements.
$k^{-5/3}$ scaling, reminiscent of the atmospheric spectra of Nastrom & Gage and (b) at the higher of the Rossby numbers considered a minimum is seen in the vertical shear spectrum, reminiscent of similar spectra obtained using in situ measurements.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 20
- Cited by

