1. Introduction
Turbulent rotating convection is ubiquitous in geo- and astrophysical objects, and often directly controls observable features. A prime example is planetary magnetic fields, which are generated by convective flows in electrically conducting regions deep inside the planetary interior (Jones Reference Jones2011). Coriolis forces are essential in this so-called dynamo process, as they induce the spatial correlations needed for large-scale magnetic field generation. Further examples include the alternating zonal wind patterns that shape the surfaces of giant planets (Heimpel, Aurnou & Wicht Reference Heimpel, Aurnou and Wicht2005; Kaspi et al. Reference Kaspi2023) and the thermohaline ocean circulation on Earth, where deep and intermediate water masses are formed by rotationally influenced open ocean convection (Marshall & Schott Reference Marshall and Schott1999). Rotating convection also occurs in the subsurface oceans of icy moons, where it may affect the properties of the crust (Soderlund et al. Reference Soderlund2020), in planetary magma oceans, where it controls crystallisation dynamics (Maas & Hansen Reference Maas and Hansen2019), and in stellar interiors (Fan Reference Fan2021).
Developing a thorough physical understanding of these systems has been plagued by the fact that the relevant parameter regime is difficult to explore in both numerical simulations and laboratory experiments. The problem is illustrated in figure 1. Natural systems tend to be highly turbulent, yet they typically remain affected by Coriolis forces. Denoting the depth of the convection zone by
$H$
, the typical flow speed by
$U$
and kinematic viscosity by
$\nu$
, the Reynolds number
$ \textit{Re}_{\kern-1pt H} = \textit{UH} / \nu$
is usually huge, while the flow field still evolves on a time scale
$H/U$
that exceeds the rotation period
$\Omega ^{-1}$
. Coriolis forces thus remain important and the Rossby number
$\textit{Ro}_{\kern-1pt H} = U / 2\varOmega H$
is small. Increasing
$\textit{Re}_{\kern-1pt H}$
while simultaneously keeping
$\textit{Ro}_{\kern-1.2pt H}$
small requires progressively smaller values of their ratio
$\textit{Ek} = {\textit{Ro}_{\kern-1pt H}} / {\textit{Re}_{\kern-1pt H}} = \nu / 2\varOmega H^2$
. This parameter, known as the Ekman number, compares the rotation period with the time scale of viscous friction.
Figure 1. A sketch of the parameter space governing rotating convection. Natural systems are highly turbulent (high Reynolds number
$\textit{Re}_{\kern-1pt H}\kern-0.9pt)$
and rotationally influenced (Rossby number
$\textit{Ro}_{\kern-1pt H} \lt 1$
, region below the green line). Experiments (yellow shaded area), numerical dynamo models (grey area) and previous simulations of non-magnetic convection (purple area) have failed to reach realistic conditions. As demonstrated in a new paper by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025), a properly rescaled version of the Boussinesq equations for the rotating Rayleigh–Bénard system (Julien et al. Reference Julien, van Kan, Miquel, Knobloch and Vasil2024) allows for DNS at previously impossible parameter values (cyan diamonds). The red line marks the location where the thermal boundary layers are expected to lose rotational control. Figure from van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025).
Geo- and astrophysical systems typically meet these conditions because of their enormous spatial scale
$H$
. Laboratory experiments, even ‘big’ ones like the 4 m tall TROCONVEX experiment at Eindhoven University (Cheng et al. Reference Cheng, Aurnou, Julien and Kunnen2018), have to increase the rotation rate along with the flow amplitude to preserve the rotational influence. Centrifugal forces inevitably become dynamically important at some point, which limits the achievable Ekman numbers. Direct numerical simulations (DNS) on the other hand suffer from the fact that the range of length and time scales involved quickly broadens with decreasing
$\textit{Ek}$
, which also limits the accessible parameter values.
New work by van Kan et al. represents a breakthrough in this context, as nicely illustrated by the cyan diamonds in figure 1. The authors present numerical simulations down to
$ \textit{Ek} = 10^{-15}$
, matching the value estimated for the Earth’s core. This Ekman number is more than six orders of magnitude smaller than the most extreme value reached in previous studies (Song, Shishkina & Zhu Reference Song, Shishkina and Zhu2024). The new results were obtained for the rotating Rayleigh–Bénard system, a plane, horizontal fluid layer heated from below, cooled from above and rotating about a vertical axis. The configuration thus approximates the conditions close to the poles of planets and stars.
2. The benefits of proper scaling
It is instructive to trace the route that has led to this remarkable progress. The rapidly rotating regime is apparently so difficult to explore numerically because the range of temporal and spatial scales involved quickly expands with decreasing Ekman number. Convective instabilities are characterised by a tiny horizontal scale that is
$O(\textit{Ek}^{-1/3})$
times smaller than the system scale
$H$
(Chandrasekhar Reference Chandrasekhar1961), and the associated horizontal and vertical diffusion times differ by a huge factor of
$ \textit{Ek}^{-2/3}$
. Fast inertial waves introduce even shorter time scales and increase the ratio of slow to fast time scales to
$O(\textit{Ek}^{-1})$
. For an Earth-like value of
$ \textit{Ek}=10^{-15}$
, these scale differences are daunting.
Interestingly, the very same scale disparities that severely limit current DNS can be exploited by asymptotic reduction techniques, an approach pioneered by Keith Julien and co-workers (Julien, Knobloch & Werne Reference Julien, Knobloch and Werne1998; Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006). Using scales that reflect the expected properties of the solution, and introducing
$\epsilon = \textit{Ek}^{1/3}$
as a small parameter, a closed system of reduced equations can be derived that is formally valid in the asymptotic limit
$ \textit{Ek},\textit{Ro}_{\kern-1pt H} \rightarrow 0$
. Fast inertial modes are filtered out in this process. Simulations using this asymptotic model have provided substantial insight into the physics of rapidly rotating convection, covering flows ranging from weakly nonlinear to highly turbulent (Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
,Reference Julien, Rubio, Grooms and Knobloch
b
; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014). A weakness of such models is that all scales, down to the smallest ones, are implicitly assumed to be geostrophically balanced to leading order – an unrealistic scenario for many natural systems.
Van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) apply a rescaling similar to the one used in the asymptotic model to the full Boussinesq equations and demonstrate that many of the attractive features are preserved. In particular, as shown in a companion paper (Julien et al. Reference Julien, van Kan, Miquel, Knobloch and Vasil2024), the rescaling drastically improves numerical conditioning, which eliminates spurious modes that otherwise cause numerical instabilities at low
$\textit{Ek}$
. In contrast to the asymptotic model, fast inertial modes are retained and require an implicit treatment of the Coriolis force to avoid an overly restrictive Courant–Friedrichs–Lewy condition. There is still the problem that, for
$ \textit{Ek} \ll 1$
, the horizontally averaged temperature profile evolves on a much slower time scale than the convective flow. A final trick, also borrowed from the asymptotic model, provides a remedy. It can be shown that for wide domains, the time derivative term in the mean temperature equation becomes subdominant in statistically stationary states. Neglecting it vastly reduces the computational resources that need to be spent on transients.
3. New insights
The new rescaling approach allows the authors to explore uncharted territory in parameter space and to tackle questions that were open to speculation. In particular, it allows them to bridge the gap between previous DNS and the asymptotic model. The new results agree with existing DNS for moderate Ekman numbers, and match those obtained with the asymptotic model for sufficiently small
$\textit{Ek}$
. The transition to asymptotic behaviour can thus be analysed in detail, which was impossible until now.
An exciting feature of turbulent, rotating convection, first observed in the reduced model (Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b
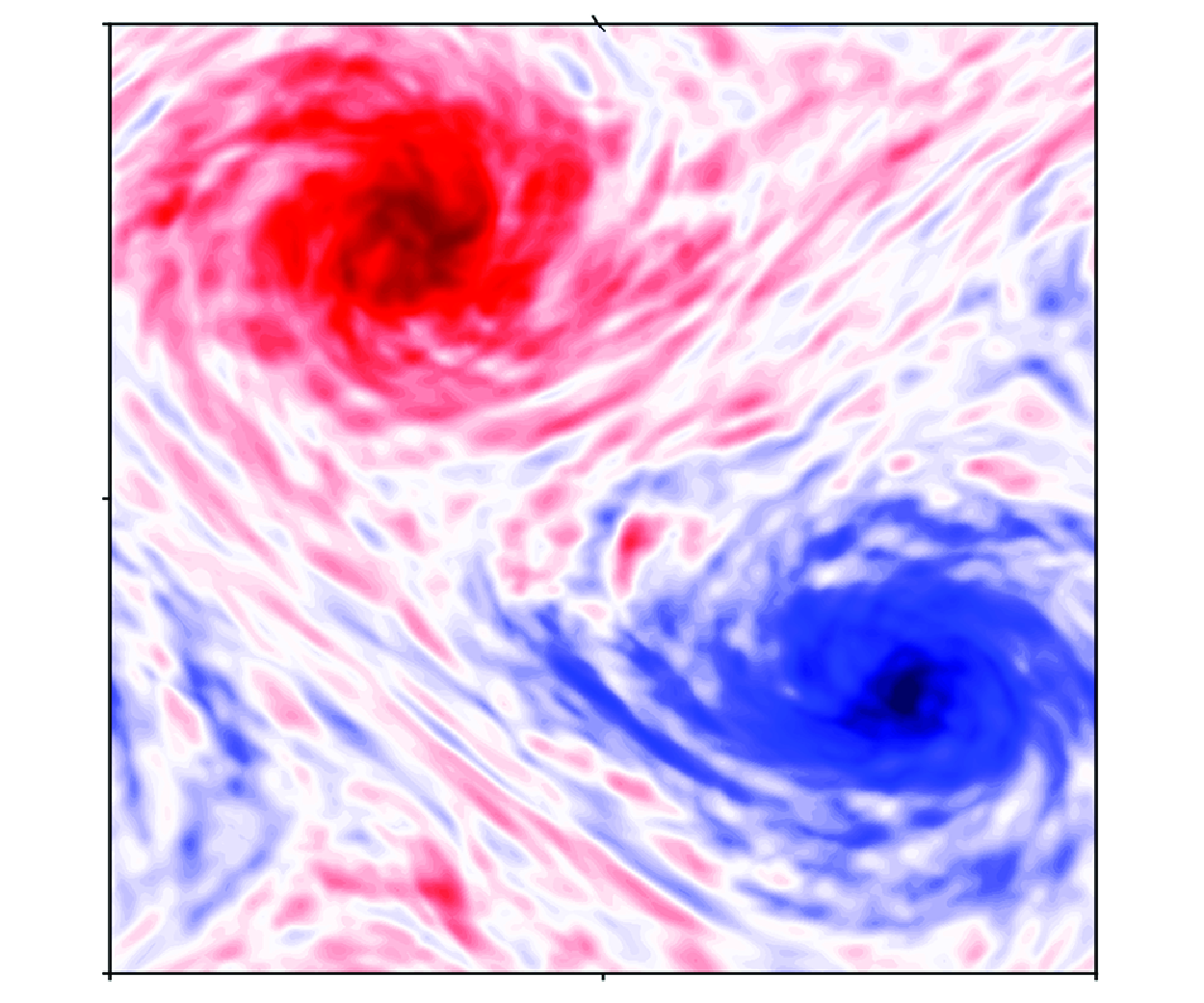
; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014) and later reproduced in DNS (Favier, Silvers & Proctor Reference Favier, Silvers and Proctor2014; Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), are inverse energy cascades that result in the formation of large-scale barotropic vortices. However, while the asymptotic model predicted a dipolar pair of equally strong cyclones and anticyclones, DNS only produced strong cyclones, with the anticyclones remaining weaker and diffuse. The simulations by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) nicely show the transition from one regime to the other, as illustrated in figure 2.
The new approach allows one to study how exactly asymptotic behaviour is lost as finite-Ekman-number effects become influential. Loss of rotational control of the thermal boundary layer while the bulk flow remains rotationally constrained is particularly important in this context (Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
). By definition, the asymptotic model is unsuitable to investigate such states, but the rescaled DNS now finally shed light on this issue.
4. Outlook
The results presented by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) just scratch the surface of what we may expect to learn from similar studies in upcoming years. Previous simulations of rotating convective turbulence were limited to moderate Reynolds numbers because the Ekman numbers necessary to maintain rotational control for larger values of
$\textit{Re}_{\kern-1pt H}$
could not be reached. This limitation has now been lifted, which opens the door for exciting future research.
The Rayleigh–Bénard configuration represents the Drosophila of convective fluid systems (Lohse Reference Lohse2024) and has a long tradition in spawning innovative new ideas and concepts that are subsequently generalised to more complicated systems. It thus seems natural to extend the recent rescaling ideas to models that include additional effects, such as a rotation axis that is tilted with respect to gravity, Ekman pumping or magnetic fields – in a similar manner to the asymptotic techniques that have already been applied to these systems (Calkins et al. Reference Calkins, Julien, Tobias and Aurnou2015; Julien et al. Reference Julien, Aurnou, Calkins, Knobloch, Marti, Stellmach and Vasil2016; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2016; Tro, Grooms & Julien Reference Tro, Grooms and Julien2024). Finally, many models in geo- and astrophysics are designed to resemble natural systems as closely as possible, and sphericity is key in this respect. It remains to be seen what can be learned for these kinds of models.
$5 \times 10^{13}$
. J. Fluid Mech. 989, A3.10.1017/jfm.2024.484CrossRefGoogle Scholar
$\textit{Re}_{\kern-1pt H}\kern-0.9pt)$ and rotationally influenced (Rossby number 
$\textit{Ro}_{\kern-1pt H} \lt 1$, region below the green line). Experiments (yellow shaded area), numerical dynamo models (grey area) and previous simulations of non-magnetic convection (purple area) have failed to reach realistic conditions. As demonstrated in a new paper by van Kan et al. (2025), a properly rescaled version of the Boussinesq equations for the rotating Rayleigh–Bénard system (Julien et al.2024) allows for DNS at previously impossible parameter values (cyan diamonds). The red line marks the location where the thermal boundary layers are expected to lose rotational control. Figure from van Kan et al. (2025).
$z$ component of vorticity 
$\overline {\omega _z}$ for (a) 
$ \textit{Ek}=10^{-15}$ and (b) 
$ \textit{Ek}=10^{-6}$. While a symmetric pair of vortices is found at small 
$\textit{Ek}$, cyclonic vorticity dominates at moderate 
$\textit{Ek}$. (c) The skewness of 
$\overline {\omega _z}$ as a function of Ekman number, which reveals how the asymmetry vanishes with decreasing 
$\textit{Ek}$. The Prandtl number is one in all cases, and the super-criticality is identical. For the exact definition of the quantities shown and the control parameters used, we refer to the original paper by van Kan et al. (2025), from which all images have been taken.
You have
Access
Open access
1. Introduction
Turbulent rotating convection is ubiquitous in geo- and astrophysical objects, and often directly controls observable features. A prime example is planetary magnetic fields, which are generated by convective flows in electrically conducting regions deep inside the planetary interior (Jones Reference Jones2011). Coriolis forces are essential in this so-called dynamo process, as they induce the spatial correlations needed for large-scale magnetic field generation. Further examples include the alternating zonal wind patterns that shape the surfaces of giant planets (Heimpel, Aurnou & Wicht Reference Heimpel, Aurnou and Wicht2005; Kaspi et al. Reference Kaspi2023) and the thermohaline ocean circulation on Earth, where deep and intermediate water masses are formed by rotationally influenced open ocean convection (Marshall & Schott Reference Marshall and Schott1999). Rotating convection also occurs in the subsurface oceans of icy moons, where it may affect the properties of the crust (Soderlund et al. Reference Soderlund2020), in planetary magma oceans, where it controls crystallisation dynamics (Maas & Hansen Reference Maas and Hansen2019), and in stellar interiors (Fan Reference Fan2021).
Developing a thorough physical understanding of these systems has been plagued by the fact that the relevant parameter regime is difficult to explore in both numerical simulations and laboratory experiments. The problem is illustrated in figure 1. Natural systems tend to be highly turbulent, yet they typically remain affected by Coriolis forces. Denoting the depth of the convection zone by
$H$
, the typical flow speed by
$U$
and kinematic viscosity by
$\nu$
, the Reynolds number
$ \textit{Re}_{\kern-1pt H} = \textit{UH} / \nu$
is usually huge, while the flow field still evolves on a time scale
$H/U$
that exceeds the rotation period
$\Omega ^{-1}$
. Coriolis forces thus remain important and the Rossby number
$\textit{Ro}_{\kern-1pt H} = U / 2\varOmega H$
is small. Increasing
$\textit{Re}_{\kern-1pt H}$
while simultaneously keeping
$\textit{Ro}_{\kern-1.2pt H}$
small requires progressively smaller values of their ratio
$\textit{Ek} = {\textit{Ro}_{\kern-1pt H}} / {\textit{Re}_{\kern-1pt H}} = \nu / 2\varOmega H^2$
. This parameter, known as the Ekman number, compares the rotation period with the time scale of viscous friction.
Figure 1. A sketch of the parameter space governing rotating convection. Natural systems are highly turbulent (high Reynolds number
$\textit{Re}_{\kern-1pt H}\kern-0.9pt)$
and rotationally influenced (Rossby number
$\textit{Ro}_{\kern-1pt H} \lt 1$
, region below the green line). Experiments (yellow shaded area), numerical dynamo models (grey area) and previous simulations of non-magnetic convection (purple area) have failed to reach realistic conditions. As demonstrated in a new paper by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025), a properly rescaled version of the Boussinesq equations for the rotating Rayleigh–Bénard system (Julien et al. Reference Julien, van Kan, Miquel, Knobloch and Vasil2024) allows for DNS at previously impossible parameter values (cyan diamonds). The red line marks the location where the thermal boundary layers are expected to lose rotational control. Figure from van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025).
Geo- and astrophysical systems typically meet these conditions because of their enormous spatial scale
$H$
. Laboratory experiments, even ‘big’ ones like the 4 m tall TROCONVEX experiment at Eindhoven University (Cheng et al. Reference Cheng, Aurnou, Julien and Kunnen2018), have to increase the rotation rate along with the flow amplitude to preserve the rotational influence. Centrifugal forces inevitably become dynamically important at some point, which limits the achievable Ekman numbers. Direct numerical simulations (DNS) on the other hand suffer from the fact that the range of length and time scales involved quickly broadens with decreasing
$\textit{Ek}$
, which also limits the accessible parameter values.
New work by van Kan et al. represents a breakthrough in this context, as nicely illustrated by the cyan diamonds in figure 1. The authors present numerical simulations down to
$ \textit{Ek} = 10^{-15}$
, matching the value estimated for the Earth’s core. This Ekman number is more than six orders of magnitude smaller than the most extreme value reached in previous studies (Song, Shishkina & Zhu Reference Song, Shishkina and Zhu2024). The new results were obtained for the rotating Rayleigh–Bénard system, a plane, horizontal fluid layer heated from below, cooled from above and rotating about a vertical axis. The configuration thus approximates the conditions close to the poles of planets and stars.
2. The benefits of proper scaling
It is instructive to trace the route that has led to this remarkable progress. The rapidly rotating regime is apparently so difficult to explore numerically because the range of temporal and spatial scales involved quickly expands with decreasing Ekman number. Convective instabilities are characterised by a tiny horizontal scale that is
$O(\textit{Ek}^{-1/3})$
times smaller than the system scale
$H$
(Chandrasekhar Reference Chandrasekhar1961), and the associated horizontal and vertical diffusion times differ by a huge factor of
$ \textit{Ek}^{-2/3}$
. Fast inertial waves introduce even shorter time scales and increase the ratio of slow to fast time scales to
$O(\textit{Ek}^{-1})$
. For an Earth-like value of
$ \textit{Ek}=10^{-15}$
, these scale differences are daunting.
Interestingly, the very same scale disparities that severely limit current DNS can be exploited by asymptotic reduction techniques, an approach pioneered by Keith Julien and co-workers (Julien, Knobloch & Werne Reference Julien, Knobloch and Werne1998; Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006). Using scales that reflect the expected properties of the solution, and introducing
$\epsilon = \textit{Ek}^{1/3}$
as a small parameter, a closed system of reduced equations can be derived that is formally valid in the asymptotic limit
$ \textit{Ek},\textit{Ro}_{\kern-1pt H} \rightarrow 0$
. Fast inertial modes are filtered out in this process. Simulations using this asymptotic model have provided substantial insight into the physics of rapidly rotating convection, covering flows ranging from weakly nonlinear to highly turbulent (Sprague et al. Reference Sprague, Julien, Knobloch and Werne2006; Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a
,Reference Julien, Rubio, Grooms and Knobloch
b
; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014). A weakness of such models is that all scales, down to the smallest ones, are implicitly assumed to be geostrophically balanced to leading order – an unrealistic scenario for many natural systems.
Van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) apply a rescaling similar to the one used in the asymptotic model to the full Boussinesq equations and demonstrate that many of the attractive features are preserved. In particular, as shown in a companion paper (Julien et al. Reference Julien, van Kan, Miquel, Knobloch and Vasil2024), the rescaling drastically improves numerical conditioning, which eliminates spurious modes that otherwise cause numerical instabilities at low
$\textit{Ek}$
. In contrast to the asymptotic model, fast inertial modes are retained and require an implicit treatment of the Coriolis force to avoid an overly restrictive Courant–Friedrichs–Lewy condition. There is still the problem that, for
$ \textit{Ek} \ll 1$
, the horizontally averaged temperature profile evolves on a much slower time scale than the convective flow. A final trick, also borrowed from the asymptotic model, provides a remedy. It can be shown that for wide domains, the time derivative term in the mean temperature equation becomes subdominant in statistically stationary states. Neglecting it vastly reduces the computational resources that need to be spent on transients.
3. New insights
The new rescaling approach allows the authors to explore uncharted territory in parameter space and to tackle questions that were open to speculation. In particular, it allows them to bridge the gap between previous DNS and the asymptotic model. The new results agree with existing DNS for moderate Ekman numbers, and match those obtained with the asymptotic model for sufficiently small
$\textit{Ek}$
. The transition to asymptotic behaviour can thus be analysed in detail, which was impossible until now.
Figure 2. Vertically averaged
$z$
component of vorticity
$\overline {\omega _z}$
for (a)
$ \textit{Ek}=10^{-15}$
and (b)
$ \textit{Ek}=10^{-6}$
. While a symmetric pair of vortices is found at small
$\textit{Ek}$
, cyclonic vorticity dominates at moderate
$\textit{Ek}$
. (c) The skewness of
$\overline {\omega _z}$
as a function of Ekman number, which reveals how the asymmetry vanishes with decreasing
$\textit{Ek}$
. The Prandtl number is one in all cases, and the super-criticality is identical. For the exact definition of the quantities shown and the control parameters used, we refer to the original paper by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025), from which all images have been taken.
An exciting feature of turbulent, rotating convection, first observed in the reduced model (Julien et al. Reference Julien, Rubio, Grooms and Knobloch2012b ; Rubio et al. Reference Rubio, Julien, Knobloch and Weiss2014) and later reproduced in DNS (Favier, Silvers & Proctor Reference Favier, Silvers and Proctor2014; Guervilly, Hughes & Jones Reference Guervilly, Hughes and Jones2014; Stellmach et al. Reference Stellmach, Lischper, Julien, Vasil, Cheng, Ribeiro, King and Aurnou2014), are inverse energy cascades that result in the formation of large-scale barotropic vortices. However, while the asymptotic model predicted a dipolar pair of equally strong cyclones and anticyclones, DNS only produced strong cyclones, with the anticyclones remaining weaker and diffuse. The simulations by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) nicely show the transition from one regime to the other, as illustrated in figure 2.
The new approach allows one to study how exactly asymptotic behaviour is lost as finite-Ekman-number effects become influential. Loss of rotational control of the thermal boundary layer while the bulk flow remains rotationally constrained is particularly important in this context (Julien et al. Reference Julien, Knobloch, Rubio and Vasil2012a ). By definition, the asymptotic model is unsuitable to investigate such states, but the rescaled DNS now finally shed light on this issue.
4. Outlook
The results presented by van Kan et al. (Reference van Kan, Julien, Miquel and Knobloch2025) just scratch the surface of what we may expect to learn from similar studies in upcoming years. Previous simulations of rotating convective turbulence were limited to moderate Reynolds numbers because the Ekman numbers necessary to maintain rotational control for larger values of
$\textit{Re}_{\kern-1pt H}$
could not be reached. This limitation has now been lifted, which opens the door for exciting future research.
The Rayleigh–Bénard configuration represents the Drosophila of convective fluid systems (Lohse Reference Lohse2024) and has a long tradition in spawning innovative new ideas and concepts that are subsequently generalised to more complicated systems. It thus seems natural to extend the recent rescaling ideas to models that include additional effects, such as a rotation axis that is tilted with respect to gravity, Ekman pumping or magnetic fields – in a similar manner to the asymptotic techniques that have already been applied to these systems (Calkins et al. Reference Calkins, Julien, Tobias and Aurnou2015; Julien et al. Reference Julien, Aurnou, Calkins, Knobloch, Marti, Stellmach and Vasil2016; Plumley et al. Reference Plumley, Julien, Marti and Stellmach2016; Tro, Grooms & Julien Reference Tro, Grooms and Julien2024). Finally, many models in geo- and astrophysics are designed to resemble natural systems as closely as possible, and sphericity is key in this respect. It remains to be seen what can be learned for these kinds of models.
Declaration of interests
The author reports no conflict of interest.