Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sarman, Sten
and
Laaksonen, Aatto
2014.
Director alignment relative to the temperature gradient in nematic liquid crystals studied by molecular dynamics simulation.
Phys. Chem. Chem. Phys.,
Vol. 16,
Issue. 28,
p.
14741.
Ho, Bo-Yan
Su, Hsien-Pin
Tseng, Yu-Pei
Wu, Shin-Tson
and
Hwang, Shug-June
2015.
Temperature effects of Mach-Zehnder interferometer using a liquid crystal-filled fiber.
Optics Express,
Vol. 23,
Issue. 26,
p.
33588.
Kim, Yun Ho
Gim, Min-Jun
Jung, Hee-Tae
and
Yoon, Dong Ki
2015.
Periodic arrays of liquid crystalline torons in microchannels.
RSC Advances,
Vol. 5,
Issue. 25,
p.
19279.
Narezo Guzman, Daniela
Xie, Yanbo
Chen, Songyue
Fernandez Rivas, David
Sun, Chao
Lohse, Detlef
and
Ahlers, Guenter
2016.
Heat-flux enhancement by vapour-bubble nucleation in Rayleigh–Bénard turbulence.
Journal of Fluid Mechanics,
Vol. 787,
Issue. ,
p.
331.
Humayun, Muhammad Hamza
Sultan Shah Bukhari, Syed
Zakwan, Muhammad
Bayer, Mustafa Mert
Gökay, Ulaş Sabahattın
Serpengüzel, Ali
Taıra, Kenıchı
Omura, Etsuji
and
Nakata, Josuke
2017.
Spatial intensity profiling of elastic and inelastic scattering in isotropic and anisotropic liquids by immersion of a spherical silicon photocell.
Applied Optics,
Vol. 56,
Issue. 34,
p.
9384.
Quint, Makiko T.
Sarang, Som
Quint, David A.
Keshavarz, Amir
Stokes, Benjamin J.
Subramaniam, Anand Bala
Huang, Kerwyn Casey
Gopinathan, Ajay
Hirst, Linda S.
and
Ghosh, Sayantani
2017.
Plasmon-actuated nano-assembled microshells.
Scientific Reports,
Vol. 7,
Issue. 1,
Takenaka, Y.
and
Yamamoto, T.
2017.
Light-induced displacement of a microbead through the thermal expansion of liquid crystals.
Soft Matter,
Vol. 13,
Issue. 6,
p.
1116.
Škarabot, M.
Osterman, N.
and
Muševič, I.
2017.
Optothermally driven colloidal transport in a confined nematic liquid crystal.
Soft Matter,
Vol. 13,
Issue. 13,
p.
2448.
Buka, Ágnes
and
Éber, Nándor
2018.
Reference Module in Materials Science and Materials Engineering.
MIYAMOTO, Yoshiaki
NISHIZAWA, Seiya
and
TOMITA, Hirofumi
2020.
Impacts of Number of Cloud Condensation Nuclei on Two-Dimensional Moist Rayleigh Convection.
Journal of the Meteorological Society of Japan. Ser. II,
Vol. 98,
Issue. 2,
p.
437.
Sasa, Shin-ichi
Nakagawa, Naoko
Itami, Masato
and
Nakayama, Yohei
2021.
Stochastic order parameter dynamics for phase coexistence in heat conduction.
Physical Review E,
Vol. 103,
Issue. 6,
Kobayashi, Michikazu
Nakagawa, Naoko
and
Sasa, Shin-ichi
2023.
Control of Metastable States by Heat Flux in the Hamiltonian Potts Model.
Physical Review Letters,
Vol. 130,
Issue. 24,
Sasa, Shin-ichi
and
Nakagawa, Naoko
2025.
Non-equilibrium Phase Coexistence in Boundary-Driven Diffusive Systems.
Journal of Statistical Physics,
Vol. 192,
Issue. 2,
Vanarse, Vinod Babasaheb
Thakur, Siddharth
and
Bandyopadhyay, Dipankar
2025.
Recirculatory Solvotaxis of a Nematic Droplet on Water Surface Enabling Miniaturization.
Langmuir,
Vol. 41,
Issue. 9,
p.
5933.
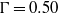 $\Gamma = 0. 50$ ). The difference between the top and bottom plate temperature
$\Gamma = 0. 50$ ). The difference between the top and bottom plate temperature 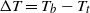 $ \mathrm{\Delta} T= {T}_{b} - {T}_{t} $ was held constant, while the average temperature
$ \mathrm{\Delta} T= {T}_{b} - {T}_{t} $ was held constant, while the average temperature  ${T}_{m} = ({T}_{b} + {T}_{t} )/ 2$ was varied. There was a significant increase of the transported heat when the phase transition temperature
${T}_{m} = ({T}_{b} + {T}_{t} )/ 2$ was varied. There was a significant increase of the transported heat when the phase transition temperature 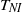 ${T}_{NI} $ was between
${T}_{NI} $ was between 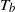 ${T}_{b} $ and
${T}_{b} $ and 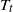 ${T}_{t} $ . Measurements of the temperatures along the sidewall of the sample as a function of
${T}_{t} $ . Measurements of the temperatures along the sidewall of the sample as a function of 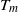 ${T}_{m} $ showed several ranges with qualitatively different behaviour of quantities such as the time-averaged sidewall temperature, temperature gradient, or temperature fluctuations. We interpret these different ranges in terms of properties of the thermal boundary layers close to the top and bottom plates whose stability and nature depends on the location within the sample of
${T}_{m} $ showed several ranges with qualitatively different behaviour of quantities such as the time-averaged sidewall temperature, temperature gradient, or temperature fluctuations. We interpret these different ranges in terms of properties of the thermal boundary layers close to the top and bottom plates whose stability and nature depends on the location within the sample of 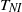 ${T}_{NI} $ .
${T}_{NI} $ .
