Article contents
Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition
Published online by Cambridge University Press: 19 March 2013
Abstract
A model is developed for describing mixing of several species under high-pressure conditions. The model includes the Peng–Robinson equation of state, a full mass-diffusion matrix, a full thermal-diffusion-factor matrix necessary to incorporate the Soret and Dufour effects and both thermal conductivity and viscosity computed for the species mixture using mixing rules. Direct numerical simulations (DNSs) are conducted in a temporal mixing layer configuration. The initial mean flow is perturbed using an analytical perturbation which is consistent with the definition of vorticity and is divergence free. Simulations are performed for a set of five species relevant to hydrocarbon combustion and an ensemble of realizations is created to explore the effect of the initial Reynolds number and of the initial pressure. Each simulation reaches a transitional state having turbulent characteristics and most of the data analysis is performed on that state. A mathematical reformulation of the flux terms in the conservation equations allows the definition of effective species-specific Schmidt numbers 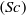 $(\mathit{Sc})$ and of an effective Prandtl number
$(\mathit{Sc})$ and of an effective Prandtl number 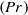 $(\mathit{Pr})$ based on effective species-specific diffusivities and an effective thermal conductivity, respectively. Because these effective species-specific diffusivities and the effective thermal conductivity are not directly computable from the DNS solution, we develop models for both of these quantities that prove very accurate when compared with the DNS database. For two of the five species, values of the effective species-specific diffusivities are negative at some locations indicating that these species experience spinodal decomposition; we determine the necessary and sufficient condition for spinodal decomposition to occur. We also show that flows displaying spinodal decomposition have enhanced vortical characteristics and trace this aspect to the specific features of high-density-gradient magnitude regions formed in the flows. The largest values of the effective species-specific
$(\mathit{Pr})$ based on effective species-specific diffusivities and an effective thermal conductivity, respectively. Because these effective species-specific diffusivities and the effective thermal conductivity are not directly computable from the DNS solution, we develop models for both of these quantities that prove very accurate when compared with the DNS database. For two of the five species, values of the effective species-specific diffusivities are negative at some locations indicating that these species experience spinodal decomposition; we determine the necessary and sufficient condition for spinodal decomposition to occur. We also show that flows displaying spinodal decomposition have enhanced vortical characteristics and trace this aspect to the specific features of high-density-gradient magnitude regions formed in the flows. The largest values of the effective species-specific 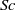 $\mathit{Sc}$ numbers can be well in excess of those known for gases but almost two orders of magnitude smaller than those of liquids at atmospheric pressure. The effective thermal conductivity also exhibits negative values at some locations and the effective
$\mathit{Sc}$ numbers can be well in excess of those known for gases but almost two orders of magnitude smaller than those of liquids at atmospheric pressure. The effective thermal conductivity also exhibits negative values at some locations and the effective 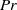 $\mathit{Pr}$ displays values that can be as high as those of a liquid refrigerant. Examination of the equivalence ratio indicates that the stoichiometric region is thin and coincides with regions where the mixture effective species-specific Lewis number values are well in excess of unity. Very lean and very rich regions coexist in the vicinity of the stoichiometric region. Analysis of the dissipation indicates that it is dominated by mass diffusion, with viscous dissipation being the smallest among the three dissipation modes. The sum of the heat and species (i.e. scalar) dissipation is functionally modelled using the effective species-specific diffusivities and the effective thermal conductivity. Computations of the modelled sum employing the modelled effective species-specific diffusivities and the modelled effective thermal conductivity shows that it accurately replicates the exact equivalent dissipation.
$\mathit{Pr}$ displays values that can be as high as those of a liquid refrigerant. Examination of the equivalence ratio indicates that the stoichiometric region is thin and coincides with regions where the mixture effective species-specific Lewis number values are well in excess of unity. Very lean and very rich regions coexist in the vicinity of the stoichiometric region. Analysis of the dissipation indicates that it is dominated by mass diffusion, with viscous dissipation being the smallest among the three dissipation modes. The sum of the heat and species (i.e. scalar) dissipation is functionally modelled using the effective species-specific diffusivities and the effective thermal conductivity. Computations of the modelled sum employing the modelled effective species-specific diffusivities and the modelled effective thermal conductivity shows that it accurately replicates the exact equivalent dissipation.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 79
- Cited by

