Article contents
The motion of a 2D pendulum in a channel subjected to an incoming flow
Published online by Cambridge University Press: 22 December 2014
Abstract
The flow around a tethered cylinder subjected to an incoming flow transverse to its main axis and confined in a channel is investigated by means of global stability analysis of the full coupled body–fluid problem. When the cylinder is strongly confined (ratio of cylinder diameter to cell height, 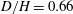 $D/H=0.66$ ) we retrieve the confinement-induced instability (CIV) discovered by Semin et al. (J. Fluid Mech., vol. 690, 2011, pp. 345–365), which sets in at a Reynolds number below the vortex-induced vibration threshold. For a moderately confined case (
$D/H=0.66$ ) we retrieve the confinement-induced instability (CIV) discovered by Semin et al. (J. Fluid Mech., vol. 690, 2011, pp. 345–365), which sets in at a Reynolds number below the vortex-induced vibration threshold. For a moderately confined case ( 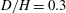 $D/H=0.3$ ), a new steady static instability is discovered, referred to as confinement-induced divergence (CID). This instability saturates into an asymmetric steady solution through a supercritical pitchfork bifurcation. In addition, the CIV and CID instabilities are studied via a reduced model obtained by considering a quasi-static response of the fluid, allowing for tracing back the physical mechanisms responsible for the instabilities.
$D/H=0.3$ ), a new steady static instability is discovered, referred to as confinement-induced divergence (CID). This instability saturates into an asymmetric steady solution through a supercritical pitchfork bifurcation. In addition, the CIV and CID instabilities are studied via a reduced model obtained by considering a quasi-static response of the fluid, allowing for tracing back the physical mechanisms responsible for the instabilities.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 3
- Cited by


