Article contents
Monopoles in a uniform zonal flow on a quasi-geostrophic 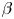 $\beta $-plane: effects of the Galilean non-invariance of the rotating shallow-water equations
$\beta $-plane: effects of the Galilean non-invariance of the rotating shallow-water equations
Published online by Cambridge University Press: 31 December 2020
Abstract
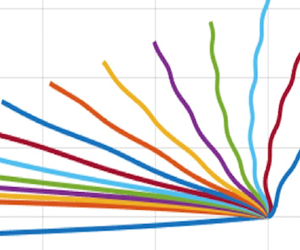
Galilean non-invariance of the shallow-water equations describing the motion of a rotating fluid implies that a homogeneous background flow modifies the dynamics of localized vortices even without the  $\beta $-effect. In particular, in a divergent quasi-geostrophic model on a
$\beta $-effect. In particular, in a divergent quasi-geostrophic model on a  $\beta $-plane, which originates from the shallow-water model, the equation of motion in the reference frame attached to a uniform zonal background flow has the same form as in the absence of this flow, but with a modified
$\beta $-plane, which originates from the shallow-water model, the equation of motion in the reference frame attached to a uniform zonal background flow has the same form as in the absence of this flow, but with a modified  $\beta $-parameter depending linearly on the flow velocity
$\beta $-parameter depending linearly on the flow velocity  $\bar{U}$. The evolution of a singular vortex (SV) embedded in such a flow consists of two stages. In the first, quasi-linear stage, the SV motion is induced by the secondary dipole (
$\bar{U}$. The evolution of a singular vortex (SV) embedded in such a flow consists of two stages. In the first, quasi-linear stage, the SV motion is induced by the secondary dipole ( $\beta $-gyres) generated in the neighbourhood of the SV. During the next, nonlinear stage, the SV merges with the
$\beta $-gyres) generated in the neighbourhood of the SV. During the next, nonlinear stage, the SV merges with the  $\beta $-gyre of opposite sign to form a compact vortex pair interacting with far-field Rossby waves radiated previously by the SV, while the other
$\beta $-gyre of opposite sign to form a compact vortex pair interacting with far-field Rossby waves radiated previously by the SV, while the other  $\beta $-gyre loses connection with the SV and disappears. In the absolute reference frame and with
$\beta $-gyre loses connection with the SV and disappears. In the absolute reference frame and with  $\beta = 0$, the SV drifts downstream and at an angle to the background flow. The SV always lags behind the background flow, with the strongest resistance during the quasi-linear stage and weakening resistance at the nonlinear stage of SV evolution. In the general case where
$\beta = 0$, the SV drifts downstream and at an angle to the background flow. The SV always lags behind the background flow, with the strongest resistance during the quasi-linear stage and weakening resistance at the nonlinear stage of SV evolution. In the general case where  $\beta \gt 0$, the SV can move both upstream (for small-to-moderate
$\beta \gt 0$, the SV can move both upstream (for small-to-moderate  $\bar{U} \gt 0$) and downstream (for
$\bar{U} \gt 0$) and downstream (for  $\bar{U} \lt 0$ or sufficiently large
$\bar{U} \lt 0$ or sufficiently large  $\bar{U} \gt 0$). Under weak-to-moderate westward and all eastward flows the SV cyclone (anticyclone) also moves northward (southward), its meridional drift increasing with
$\bar{U} \gt 0$). Under weak-to-moderate westward and all eastward flows the SV cyclone (anticyclone) also moves northward (southward), its meridional drift increasing with  $\bar{U}$.
$\bar{U}$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 6
- Cited by


