Article contents
A model for the electric field-driven flow and deformation of a drop or vesicle in strong electrolyte solutions
Published online by Cambridge University Press: 20 June 2022
Abstract
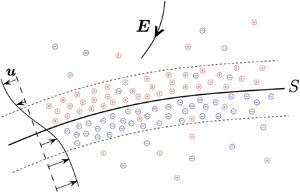
A model is constructed to describe the flow field and arbitrary deformation of a drop or vesicle that contains and is embedded in an electrolyte solution, where the flow and deformation are caused by an applied electric field. The applied field produces an electrokinetic flow, which is set up on the charge-up time scale  $\tau _{*c}=\lambda _{*} a_{*}/D_{*}$, where
$\tau _{*c}=\lambda _{*} a_{*}/D_{*}$, where  $\lambda _{*}$ is the Debye screening length,
$\lambda _{*}$ is the Debye screening length,  $a_{*}$ is the inclusion length scale and
$a_{*}$ is the inclusion length scale and  $D_{*}$ is an ion diffusion constant. The model is based on the Poisson–Nernst–Planck and Stokes equations. These are reduced or simplified by forming the limit of strong electrolytes, for which dissolved salts are completely ionised in solution, together with the limit of thin Debye layers. Debye layers of opposite polarity form on either side of the drop interface or vesicle membrane, together forming an electrical double layer. Two formulations of the model are given. One utilises an integral equation for the velocity field on the interface or membrane surface together with a pair of integral equations for the electrostatic potential on the outer faces of the double layer. The other utilises a form of the stress-balance boundary condition that incorporates the double layer structure into relations between the dependent variables on the layers’ outer faces. This constitutes an interfacial boundary condition that drives an otherwise unforced Stokes flow outside the double layer. For both formulations relations derived from the transport of ions in each Debye layer give additional boundary conditions for the potential and ion concentrations outside the double layer.
$D_{*}$ is an ion diffusion constant. The model is based on the Poisson–Nernst–Planck and Stokes equations. These are reduced or simplified by forming the limit of strong electrolytes, for which dissolved salts are completely ionised in solution, together with the limit of thin Debye layers. Debye layers of opposite polarity form on either side of the drop interface or vesicle membrane, together forming an electrical double layer. Two formulations of the model are given. One utilises an integral equation for the velocity field on the interface or membrane surface together with a pair of integral equations for the electrostatic potential on the outer faces of the double layer. The other utilises a form of the stress-balance boundary condition that incorporates the double layer structure into relations between the dependent variables on the layers’ outer faces. This constitutes an interfacial boundary condition that drives an otherwise unforced Stokes flow outside the double layer. For both formulations relations derived from the transport of ions in each Debye layer give additional boundary conditions for the potential and ion concentrations outside the double layer.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


