Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Alba, K.
Taghavi, S. M.
and
Frigaard, I. A.
2012.
Miscible density-stable displacement flows in inclined tube.
Physics of Fluids,
Vol. 24,
Issue. 12,
Redapangu, Prasanna R.
Chandra Sahu, Kirti
and
Vanka, S. P.
2012.
A study of pressure-driven displacement flow of two immiscible liquids using a multiphase lattice Boltzmann approach.
Physics of Fluids,
Vol. 24,
Issue. 10,
Moyers-Gonzalez, M.
Alba, K.
Taghavi, S.M.
and
Frigaard, I.A.
2013.
A semi-analytical closure approximation for pipe flows of two Herschel–Bulkley fluids with a stratified interface.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 193,
Issue. ,
p.
49.
Alba, K.
Taghavi, S. M.
and
Frigaard, I. A.
2013.
Miscible density-unstable displacement flows in inclined tube.
Physics of Fluids,
Vol. 25,
Issue. 6,
Taghavi, S.M.
and
Frigaard, I.A.
2013.
Estimation of mixing volumes in buoyant miscible displacement flows along near‐horizontal pipes.
The Canadian Journal of Chemical Engineering,
Vol. 91,
Issue. 3,
p.
399.
Talon, L.
Goyal, N.
and
Meiburg, E.
2013.
Variable density and viscosity, miscible displacements in horizontal Hele-Shaw cells. Part 1. Linear stability analysis.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
268.
John, M. O.
Oliveira, R. M.
Heussler, F. H. C.
and
Meiburg, E.
2013.
Variable density and viscosity, miscible displacements in horizontal Hele-Shaw cells. Part 2. Nonlinear simulations.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
295.
Alba, K.
Taghavi, S. M.
and
Frigaard, I. A.
2014.
Miscible heavy-light displacement flows in an inclined two-dimensional channel: A numerical approach.
Physics of Fluids,
Vol. 26,
Issue. 12,
Błaszczyk, Mariola M.
and
Sęk, Jerzy P.
2014.
Capillary Model of Gravity Elution of High Viscosity Liquid from a Porous Bed with a Low-Viscosity Liquid.
Transport in Porous Media,
Vol. 105,
Issue. 1,
p.
171.
Heussler, F. H. C.
Oliveira, R. M.
John, M. O.
and
Meiburg, E.
2014.
Three-dimensional Navier–Stokes simulations of buoyant, vertical miscible Hele-Shaw displacements.
Journal of Fluid Mechanics,
Vol. 752,
Issue. ,
p.
157.
Govindarajan, Rama
and
Sahu, Kirti Chandra
2014.
Instabilities in Viscosity-Stratified Flow.
Annual Review of Fluid Mechanics,
Vol. 46,
Issue. 1,
p.
331.
Zheng, Zhong
Guo, Bo
Christov, Ivan C.
Celia, Michael A.
and
Stone, Howard A.
2015.
Flow regimes for fluid injection into a confined porous medium.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
881.
Swain, Pinakinarayan A.P.
Karapetsas, George
Matar, Omar K.
and
Sahu, Kirti Chandra
2015.
Numerical simulation of pressure-driven displacement of a viscoplastic material by a Newtonian fluid using the lattice Boltzmann method.
European Journal of Mechanics - B/Fluids,
Vol. 49,
Issue. ,
p.
197.
Amiri, A.
Larachi, F.
and
Taghavi, S. M.
2016.
Buoyant miscible displacement flows in vertical pipe.
Physics of Fluids,
Vol. 28,
Issue. 10,
Moisés, G.V.L.
Naccache, M.F.
Alba, K.
and
Frigaard, I.A.
2016.
Isodense displacement flow of viscoplastic fluids along a pipe.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 236,
Issue. ,
p.
91.
Sebilleau, F.
Issa, R. I.
and
Walker, S. P.
2016.
Analysis of Turbulence Modelling Approaches to Simulate Single-phase Buoyancy Driven Counter-current Flow in a Tilted Tube.
Flow, Turbulence and Combustion,
Vol. 96,
Issue. 1,
p.
95.
Alba, K.
and
Frigaard, I.A.
2016.
Dynamics of the removal of viscoplastic fluids from inclined pipes.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 229,
Issue. ,
p.
43.
Mollaabbasi, R.
and
Taghavi, S. M.
2016.
Buoyant displacement flows in slightly non-uniform channels.
Journal of Fluid Mechanics,
Vol. 795,
Issue. ,
p.
876.
Hasnain, A.
Segura, E.
and
Alba, K.
2017.
Buoyant displacement flow of immiscible fluids in inclined pipes.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
661.
Maleki, Amir
and
Frigaard, Ian
2017.
Primary cementing of oil and gas wells in turbulent and mixed regimes.
Journal of Engineering Mathematics,
Vol. 107,
Issue. 1,
p.
201.
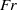 , Reynolds number
, Reynolds number 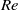 and duct inclination
and duct inclination 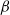 . Our results show that the flow regimes collapse into regions in a two-dimensional
. Our results show that the flow regimes collapse into regions in a two-dimensional 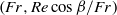 plane. These regions are qualitatively similar between pipes and plane channels, although viscous effects are more extensive in pipes. In each regime, we are able to give a leading-order estimate for the velocity of the leading displacement front, which is effectively a measure of displacement efficiency.
plane. These regions are qualitatively similar between pipes and plane channels, although viscous effects are more extensive in pipes. In each regime, we are able to give a leading-order estimate for the velocity of the leading displacement front, which is effectively a measure of displacement efficiency.
