1. Introduction
Droplet impact processes can be observed in many natural events and technical applications, such as rain, combustion chambers with a lubricating film, spray coating, cosmetic and pharmaceutical production. In the last decade, the interest in binary systems (i.e. with different liquids for droplet and impacted liquid substrate) has increased. In addition to their technical relevance, they offer the possibility to get a deeper understanding of the interaction between droplet and impacted liquid. By investigating this interaction, the question of the influence of miscibility and wettability between the droplet and the impacted liquid substrate arises.
A few studies on miscibility or wettability can be found for various droplet impact configurations, but barely any for droplet impact onto wall films. For droplet impact onto deep pools, the effect of wettability (in terms of the spreading parameter) has been studied numerically with water droplets impacting into an oil bath (Wang et al. Reference Wang, Wang, Yu and Chen2020). The authors analysed the horizontal and vertical penetrations into the oil cavity and found no significant effects of the wettability compared with those of the Weber number and the viscosity ratio for this bulky impact configuration where the droplet spreading is rather small and thus, does not favour interfacial forces in the process. Additional studies on deep pool considered different miscible and immiscible pairs with pure water, ethanol and silicone oil impacting onto water (Hasegawa & Nara Reference Hasegawa and Nara2019). However, since the liquid properties were very different, the effects of miscibility alone could not be quantified. Only a qualitative observation of a Worthington jet during the recoiling phase could clearly be attributed to the difference in miscibility. For droplet impact onto a continuous jet, the effects of wettability and miscibility were studied independently of the liquid properties by Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020). This study was carried out jointly with the present one in order to investigate the importance of the impact configuration in similar physical droplet impact processes with the same liquids. Droplet impact onto a continuous jet exhibits generally lower droplet spreading. Furthermore, the absence of a solid wall and the bulkier impact configuration lead to an impact kinetics fixed by the encapsulated drop only, and most of the effects of wettability and miscibility were observed in the recoiling phase or on the phenomenology of the impact (e.g. whether the droplet merges, is encapsulated or spreads around the jet). In the case of droplet impact onto thin wall films, which is the focus of this work, the liquid structure formed is a lamella expanding from the impact point, the so-called crown, as shown in the images of figure 1. Under certain impact conditions, the expanding crown can destabilize at the rim, leading to ejection of secondary droplets, referred to as crown-type splashing, which needs particular attention in the above mentioned applications. While the features of droplet impact onto thin wall films with similar liquids, miscible per definition, have been quite extensively studied (see e.g. the review article of Liang & Mudawar (Reference Liang and Mudawar2016)), studies on binary droplet/wall-film systems are rarely found in the literature. Originally studied in the pioneering work of Worthington & Cole (Reference Worthington and Cole1897) with water and milk, most of the studies on binary systems are with miscible liquid pairs (Thoroddsen, Etoh & Takehara Reference Thoroddsen, Etoh and Takehara2006; Geppert et al. Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016; Bernard et al. Reference Bernard, Foltyn, Geppert, Lamanna and Weigand2017; Geppert et al. Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017; Bernard et al. Reference Bernard, Geppert, Vaikuntanathan, Lamanna and Weigand2018; Kittel, Roisman & Tropea Reference Kittel, Roisman and Tropea2018b; Geppert Reference Geppert2019) and focus on splashing limit, crown dynamics or on the viscosities. In contrast, binary systems with exclusively immiscible droplet/wall-film systems have been investigated mainly with respect to the characteristics of the secondary droplets (Shaikh et al. Reference Shaikh, Toyofuku, Hoang and Marston2018) and to the repartition of the droplet and wall-film liquids in the crown depending on the viscosity ratio (Kittel, Roisman & Tropea Reference Kittel, Roisman and Tropea2018a).
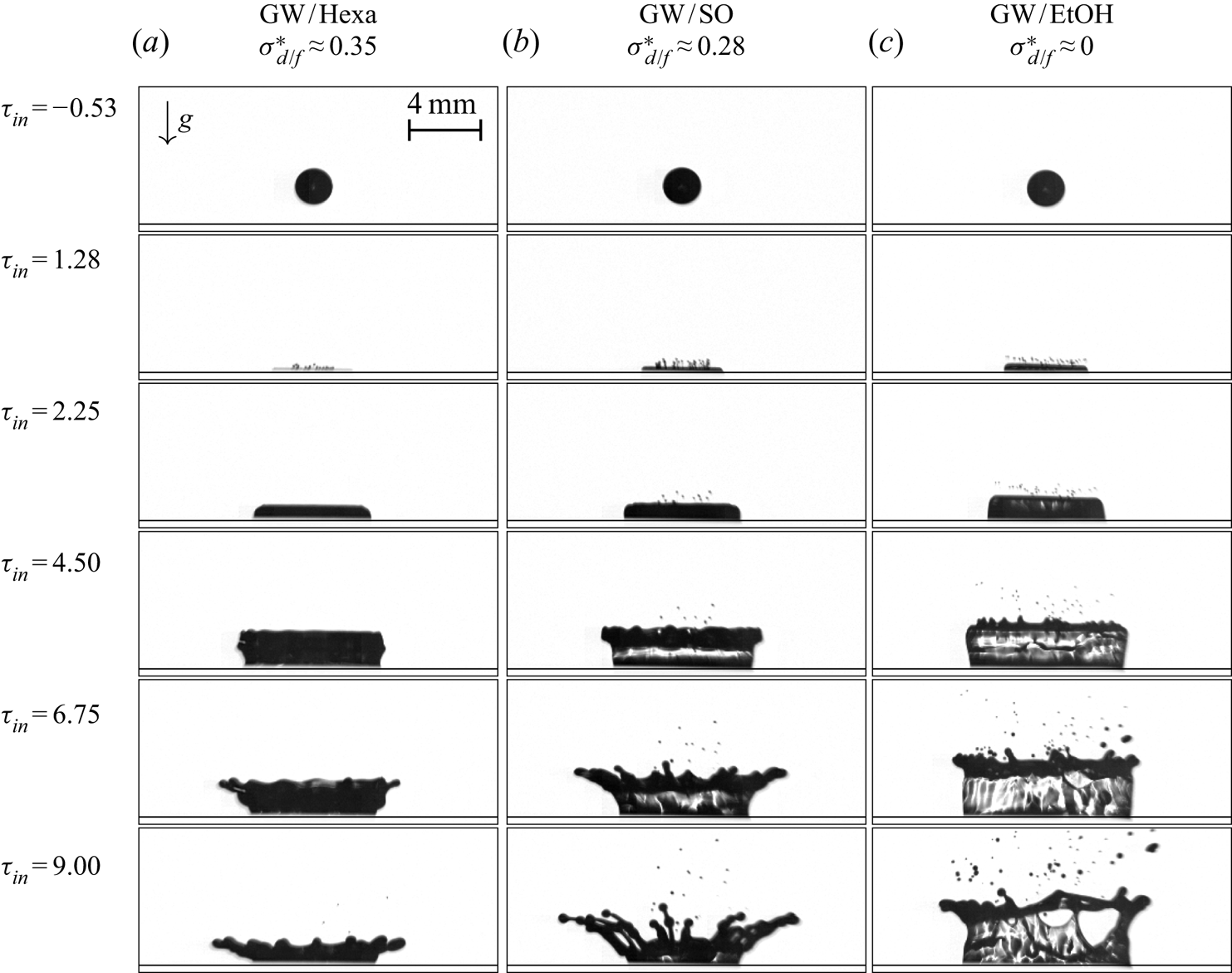
Figure 1. High-speed images of droplet impact onto wall films for three droplet/wall-film liquid pairs at similar impact conditions (see the last row of table 2 for the Weber numbers ![]() $We_{d}=363\pm 5$, and dimensionless wall-film thickness
$We_{d}=363\pm 5$, and dimensionless wall-film thickness ![]() $\delta = {{h_{f}}{}}/{{D_{d}}{}} = 0.122\pm 0.011$) at different dimensionless time instants from the impact
$\delta = {{h_{f}}{}}/{{D_{d}}{}} = 0.122\pm 0.011$) at different dimensionless time instants from the impact ![]() $\tau _{in}{}=t {V_{d}}{}/{D_{d}}{}$. Only the relative importance of the interfacial tension
$\tau _{in}{}=t {V_{d}}{}/{D_{d}}{}$. Only the relative importance of the interfacial tension ![]() $\sigma _{d/f}^{*}{}= \sigma _{d/f}{}/( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{}$) varies significantly between the liquid pairs, linked to a variation of wettability and miscibility. See § 2 for the definition of all impact parameters.
$\sigma _{d/f}^{*}{}= \sigma _{d/f}{}/( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{}$) varies significantly between the liquid pairs, linked to a variation of wettability and miscibility. See § 2 for the definition of all impact parameters.
Only few studies report directly or indirectly an effect of miscibility and wettability for droplet impacts onto wall films. Aljedaani et al. (Reference Aljedaani, Wang, Jetly and Thoroddsen2018) focused on the occurrence of holes in the crown, similar to some extent to those observed in the right-hand column of figure 1. The holes formed on the crown wall grow until they join and form a net-like structure which finally disintegrates into secondary droplets (see the movie in the supplementary material available at https://doi.org/10.1017/jfm.2020.944 of the impact process corresponding to the experiments in figure 1). This particular type of splashing event was first observed for a water/glycerol droplet impacting onto very thin wall films of ethanol (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2006) and is a unique feature of binary droplet/wall-film systems. The hole formation was attributed to Marangoni-driven flows initiated by small secondary droplets impacting onto the inside part of the crown wall (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2006; Aljedaani et al. Reference Aljedaani, Wang, Jetly and Thoroddsen2018; Kittel Reference Kittel2019). This phenomenon was also observed with very similar surface tensions for droplet and wall film (hyspin and hexadecane liquids) and was thus attributed more generally to inhomogeneities in viscosities and/or surface tensions in the crown wall (Geppert et al. Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016). Although Aljedaani et al. (Reference Aljedaani, Wang, Jetly and Thoroddsen2018) noticed only a weak reduction in the growth rate of the holes for increasing droplet viscosity, a large viscosity ratio between droplet and wall film influences the liquid repartition in the crown. For droplets with a much higher viscosity than the wall film, a two-stage crown was observed with the wall-film liquid at the upper part of the crown. Similar crown morphologies with high viscosity ratios have been observed for immiscible droplet/wall-film systems by Kittel et al. (Reference Kittel, Roisman and Tropea2018a), and can be explained by the strong differences in the time scale of the ejecta sheets coming from the droplet and the wall film (Marcotte et al. Reference Marcotte, Michon, Séon and Josserand2019). By influencing the liquid repartition inside the crown, the viscosity ratio also influences the occurrence of the holes in the crown wall. In the present study instead, the droplet and wall-film viscosities are quite similar. Hence, only one-stage crowns are observed, where the droplet is expected to cover uniformly the wall-film liquid in the crown wall. In addition to the miscible configurations leading to the formation of holes, Aljedaani et al. (Reference Aljedaani, Wang, Jetly and Thoroddsen2018) studied the impact of immiscible liquid pairs. They did not report any major differences in the crown dynamics (looking especially at the crown angle), but the hole formation vanishes despite differences in surface tension between droplet and wall film. They observed that the patch formed by the immiscible small droplets sitting on the crown wall do not grow. Holes in the crown were indeed observed only for miscible liquid pairs until now in the literature (Geppert Reference Geppert2019; Kittel Reference Kittel2019; Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2006), although Aljedaani et al. (Reference Aljedaani, Wang, Jetly and Thoroddsen2018) suggested that the hole formation could be influenced by liquid wettability of immiscible pairs. The hole formation process is not investigated in the present study, but it is encountered while studying miscibility and wettability effects with a miscible droplet/wall-film system involving glycerol, water and ethanol.
The wetting behaviour between droplet and wall film was studied by Che & Matar (Reference Che and Matar2018) with combinations of glycerol/water droplet impacting onto silicone oil and vice versa. While a Worthington jet was formed at the end of the recoiling phase for the water droplet onto the oil, it was not the case for the reversed combination. The shape of the crowns was also slightly different because of the different droplet spreading speed in the wall-film liquid. The authors state that immiscible combinations share similar features with those of miscible films without drastic differences in the impact process, which is, however, a qualitative observation.
Only Chen, Chen & Amirfazli (Reference Chen, Chen and Amirfazli2017) studied explicitly the effect of miscibility on crown formation and splashing for droplet impact onto very thin films (maximum film height of ![]() ${50}\ {\mathrm {\mu }\textrm {m}}$, i.e. 0.017 times the droplet diameter). They reported a significant role of the interfacial tension (assuming a value of zero for the miscible pair, § 2) in the receding phase, as for Che & Matar (Reference Che and Matar2018) for the wettability. They did not mention any influence for the extension phase, which is crucial for the ejection of secondary droplets, but did observe a small shift in the splashing limit. They reported that, in the case of miscible liquids, a larger Weber number (based on droplet properties) and film thickness are required to form a crown and to eject secondary droplets, however, without distinction between crown-type splashing and prompt splashing (i.e. formed as the droplet hits the surface, within the first
${50}\ {\mathrm {\mu }\textrm {m}}$, i.e. 0.017 times the droplet diameter). They reported a significant role of the interfacial tension (assuming a value of zero for the miscible pair, § 2) in the receding phase, as for Che & Matar (Reference Che and Matar2018) for the wettability. They did not mention any influence for the extension phase, which is crucial for the ejection of secondary droplets, but did observe a small shift in the splashing limit. They reported that, in the case of miscible liquids, a larger Weber number (based on droplet properties) and film thickness are required to form a crown and to eject secondary droplets, however, without distinction between crown-type splashing and prompt splashing (i.e. formed as the droplet hits the surface, within the first ![]() ${100}\ {\mathrm {\mu }}\textrm {s}$ Thoroddsen et al. (Reference Thoroddsen, Thoraval, Takehara and Etoh2011)). They explained this phenomenon by the attenuation of the kinematic discontinuity due to the absence of an interface between the droplet and wall film. In contrast, Banks et al. (Reference Banks, Ajawara, Sanchez, Surti and Aguilar2013) noted that the immiscible liquid pair FC-72 onto water required a far higher Weber number than the other miscible pairs studied for crown formation, despite having a lower viscosity and surface tension, which should rather promote splashing. They could not find a clear explanation for this, attributing the observations to either the miscibility effects or some indirect effects of viscosities on the impact morphology. The effects of the interfacial tension found on the onset of splashing in the present study could explain the observation of Banks et al. (Reference Banks, Ajawara, Sanchez, Surti and Aguilar2013).
${100}\ {\mathrm {\mu }}\textrm {s}$ Thoroddsen et al. (Reference Thoroddsen, Thoraval, Takehara and Etoh2011)). They explained this phenomenon by the attenuation of the kinematic discontinuity due to the absence of an interface between the droplet and wall film. In contrast, Banks et al. (Reference Banks, Ajawara, Sanchez, Surti and Aguilar2013) noted that the immiscible liquid pair FC-72 onto water required a far higher Weber number than the other miscible pairs studied for crown formation, despite having a lower viscosity and surface tension, which should rather promote splashing. They could not find a clear explanation for this, attributing the observations to either the miscibility effects or some indirect effects of viscosities on the impact morphology. The effects of the interfacial tension found on the onset of splashing in the present study could explain the observation of Banks et al. (Reference Banks, Ajawara, Sanchez, Surti and Aguilar2013).
The present review highlights that the question of the influence of miscibility and liquid wettability for droplet impact onto wall films remains open. To what extent can miscibility and wettability influence droplet impact onto thin wall films, especially during the extension phase?
Since droplet impact onto wall films leads to an extreme spreading of liquids, for example from 2 to 5 times the droplet diameter for the rim displacement (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020), the interface between droplet and wall-film liquids increases drastically during the extension process. Thus, the interfacial tension acting on this interface might have a significant influence on the crown dynamics. Does the interfacial tension, linked to miscibility and wettability, influence the impact process, and if yes, how? To address these questions, three droplet/wall-film liquid pairs have been chosen to vary the miscibility and wettability behaviour, as presented in § 2, leading to a variation of their interfacial tension. The differences observed between these three droplet/wall-film pairs in terms of impact outcome, crown morphology and crown kinetics are reported in § 3. From these observations, the role of the interfacial tension during crown extension is discussed in § 4. The conclusions are summarized in § 5.
2. Experimental set-up and conditions
The three different droplet/wall-film liquid pairs listed in table 1 are used to vary miscibility and liquid wettability. All the binary droplet/wall-film systems are similar, only their respective interfacial tension ![]() $\sigma _{d/f}{}$ is changing significantly so that it corresponds to immiscible liquids with partial and total wetting conditions as well as to miscible liquids. The experiments are recorded by high-speed shadowgraphy.
$\sigma _{d/f}{}$ is changing significantly so that it corresponds to immiscible liquids with partial and total wetting conditions as well as to miscible liquids. The experiments are recorded by high-speed shadowgraphy.
Table 1. Liquid properties of droplet and wall-film liquids. In the line Composition, the numbers indicate the mass percentage of G: glycerol, W: water, Hexa: n-hexadecane, S.O.: silicone oil, EtOH: ethanol. The spreading parameter ![]() $S{}$ is associated with the wettability behaviour: partial wetting (P.W.) for
$S{}$ is associated with the wettability behaviour: partial wetting (P.W.) for ![]() $S{}<0$ or full wetting (F.W.) for
$S{}<0$ or full wetting (F.W.) for ![]() $S{}>0$. The non-dimensionalized interfacial tension
$S{}>0$. The non-dimensionalized interfacial tension ![]() $\sigma _{d/f}^{*}{}$ quantifies the importance of
$\sigma _{d/f}^{*}{}$ quantifies the importance of ![]() $\sigma _{d/f}{}$ in the droplet/wall-film system.
$\sigma _{d/f}{}$ in the droplet/wall-film system.
2.1. Experimental set-up
The experimental set-up is composed of a dropper, an impact area and a high-speed imaging system. A schematic is provided in appendix A. The dropper consists of a needle (Gauge 21), connected through flexible tubes of polytetrafluoroethylene (PTFE) to a liquid reservoir. The liquid is set in motion by a peristaltic pump with a flow rate kept low enough to let a single droplet fall by gravity. The height from the wall-film surface to the needle tip is varied to obtain different droplet impact velocities ![]() ${V_{d}}{}$. The impact area is a shallow pool in which the liquid is progressively added with a micro-pipette, bounded by a metallic ring of 0.6 mm height and 60 mm diameter fixed on a sapphire plate. Sapphire is used for its high refractive index compared with the liquids used. This allows a reliable use of a confocal chromatic sensor (Micro-Epsilon, IFS2405-3) to measure the film thickness
${V_{d}}{}$. The impact area is a shallow pool in which the liquid is progressively added with a micro-pipette, bounded by a metallic ring of 0.6 mm height and 60 mm diameter fixed on a sapphire plate. Sapphire is used for its high refractive index compared with the liquids used. This allows a reliable use of a confocal chromatic sensor (Micro-Epsilon, IFS2405-3) to measure the film thickness ![]() ${h_{f}}{}$ with an accuracy of approximately 1 % for the values investigated in this work (principle described in Lel et al. Reference Lel, Kellermann, Dietze, Kneer and Pavlenko2008).
${h_{f}}{}$ with an accuracy of approximately 1 % for the values investigated in this work (principle described in Lel et al. Reference Lel, Kellermann, Dietze, Kneer and Pavlenko2008).
The imaging system is designed for high-speed shadowgraphy, recording simultaneously two orthogonal perspectives to track asymmetric features such as holes in the crown. Typical high-speed images taken with a high-speed digital video camera (Photron FASTCAM SA1.1) and LED lights operated in backlit mode can be seen in figure 1 (only one perspective is shown). The spatial and temporal resolutions of the high-speed imaging were ![]() ${80}\ \mathrm {\mu }\textrm {m}\ \textrm {px}^{-1}$ and 0.05 ms, respectively combined with an exposure time of 1/92 ms.
${80}\ \mathrm {\mu }\textrm {m}\ \textrm {px}^{-1}$ and 0.05 ms, respectively combined with an exposure time of 1/92 ms.
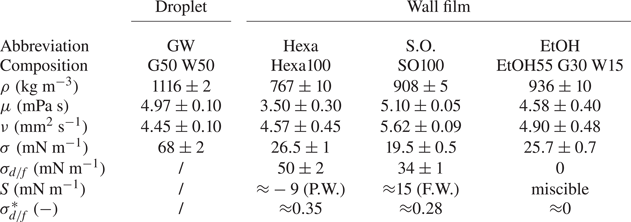
The high-speed images are post-processed with an in-house MATLAB routine that extracts the primary geometrical parameters of the crown, as detailed in appendix A. The distances between the detected four edges of the crown, like the four orange dots in the schematic of figure 2, enables the evaluation of the crown rim radius ![]() ${R_{R}}{}$ and crown base radius
${R_{R}}{}$ and crown base radius ![]() ${R_{B}}{}$ for the horizontal distances, and the crown rim height
${R_{B}}{}$ for the horizontal distances, and the crown rim height ![]() ${H_{R}}{}$ in the vertical.
${H_{R}}{}$ in the vertical.
Figure 2. Schematic of a meridional section of a crown with droplet (green) and wall-film (blue) liquids, illustrating the full coverage of the droplet liquid on the inner part of the crown. The interface between them is marked by a red line. Note that the crown thickness is not representative of the reality. The crown edges (orange dots) extracted from the post-processing are used to define the crown geometrical parameters: rim radius ![]() ${R_{R}}{}$, rim height
${R_{R}}{}$, rim height ![]() ${H_{R}}{}$ and base radius
${H_{R}}{}$ and base radius ![]() ${R_{B}}{}$.
${R_{B}}{}$.
The values of the geometrical parameters are averaged between the two perspectives of the experimental set-up to reduce the measurement uncertainty. The typical errors associated with the measurement of the crown geometrical parameters are between 1.5 % and 4.3 % for the radii, and between 1.6 % and 5.2 % for the crown height (Geppert Reference Geppert2019). The droplet diameter ![]() ${D_{d}}{}$ and impact velocity
${D_{d}}{}$ and impact velocity ![]() ${V_{d}}{}$ are also measured from the high-speed images shortly before impact (
${V_{d}}{}$ are also measured from the high-speed images shortly before impact (![]() ${\sim }1.5\ \textrm {ms}$). By adding up the systematic and random uncertainties, which maximizes the error, the overall uncertainty for the droplet diameter remains smaller than 2.8 %, and below 3 % for the impact velocity (Geppert Reference Geppert2019). A detailed description of the set-up (which has been used with the same operating conditions), the post-processing routine and the associated measurement errors can be found in Geppert et al. (Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016, Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017) and Geppert (Reference Geppert2019).
${\sim }1.5\ \textrm {ms}$). By adding up the systematic and random uncertainties, which maximizes the error, the overall uncertainty for the droplet diameter remains smaller than 2.8 %, and below 3 % for the impact velocity (Geppert Reference Geppert2019). A detailed description of the set-up (which has been used with the same operating conditions), the post-processing routine and the associated measurement errors can be found in Geppert et al. (Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016, Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017) and Geppert (Reference Geppert2019).
2.2. Variation of droplet/wall-film liquids
The liquids of the droplet/wall-film pairs have been chosen to vary the wettability and miscibility behaviours, keeping other liquid properties almost unchanged. The liquid properties are summarized in table 1, together with the abbreviations used for each liquid.
The droplet liquid is systematically composed of a mixture of glycerol and water (abbreviation GW), which is coloured with Indigotin 85 (E 132, BASF, Germany) similar to the liquids used by Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020). The only parameter varying significantly is the interfacial tension with the wall-film liquids ![]() $\sigma _{d/f}$ (see Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020) for more details on their determination), the subscript
$\sigma _{d/f}$ (see Baumgartner et al. (Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020) for more details on their determination), the subscript ![]() $d$ standing for droplet and
$d$ standing for droplet and ![]() $f$ for wall film. The interfacial tension is associated with the miscibility behaviour (
$f$ for wall film. The interfacial tension is associated with the miscibility behaviour (![]() $\sigma _{d/f}=0$ for miscible liquids) and the wettability behaviour through the spreading parameter
$\sigma _{d/f}=0$ for miscible liquids) and the wettability behaviour through the spreading parameter ![]() $S$. The spreading parameter is defined as
$S$. The spreading parameter is defined as ![]() $S{}= \sigma _d- \sigma _f- \sigma _{d/f}$, which takes negative values for partial wetting (P.W.) and positive values for full wetting (F.W.) (De Gennes, Brochard-Wyart & Quéré Reference De Gennes, Brochard-Wyart and Quéré2013). For the wettability, n-hexadecane (abbreviation Hexa, third column in table 1) provides partial wetting with aqueous solutions as is the case with many alkanes. This is confirmed by the estimation of S for GW/Hexa which is negative with approximately
$S{}= \sigma _d- \sigma _f- \sigma _{d/f}$, which takes negative values for partial wetting (P.W.) and positive values for full wetting (F.W.) (De Gennes, Brochard-Wyart & Quéré Reference De Gennes, Brochard-Wyart and Quéré2013). For the wettability, n-hexadecane (abbreviation Hexa, third column in table 1) provides partial wetting with aqueous solutions as is the case with many alkanes. This is confirmed by the estimation of S for GW/Hexa which is negative with approximately ![]() ${-9}\ \textrm {mN}\ \textrm {m}^{-1}$, and the observation of n-hexadecane lenses on top of GW (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020). In contrast, silicone oil (abbreviation S.O., fourth column in table 1) provides full wetting with aqueous solutions (Ross & Becher Reference Ross and Becher1992; De Gennes et al. Reference De Gennes, Brochard-Wyart and Quéré2013). The spreading parameter S is positive and equal to approximately 15. The full wetting behaviour is confirmed by the observation of an oil drop spreading on the surface of a liquid bath of GW (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
${-9}\ \textrm {mN}\ \textrm {m}^{-1}$, and the observation of n-hexadecane lenses on top of GW (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020). In contrast, silicone oil (abbreviation S.O., fourth column in table 1) provides full wetting with aqueous solutions (Ross & Becher Reference Ross and Becher1992; De Gennes et al. Reference De Gennes, Brochard-Wyart and Quéré2013). The spreading parameter S is positive and equal to approximately 15. The full wetting behaviour is confirmed by the observation of an oil drop spreading on the surface of a liquid bath of GW (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
The last wall-film liquid is a mixture of ethanol, water and glycerol (abbreviation EtOH, fifth column in table 1), which has been tuned to approach the two other wall-film liquid properties. The mixture of ethanol is miscible with the droplet liquid GW. In the case of miscible liquids, the interfacial tension is assumed to be zero because no interface, in a strict sense, exists between the liquids. Note that, for miscible liquids with composition gradients, ![]() $\sigma _{d/f}{}$ may transiently differ from zero before diffusion takes place (Truzzolillo & Cipelletti Reference Truzzolillo and Cipelletti2017), which may be the case for droplet impact processes of a few milliseconds. Nevertheless, the measurements of interfacial tensions for water and glycerol mixtures show values of
$\sigma _{d/f}{}$ may transiently differ from zero before diffusion takes place (Truzzolillo & Cipelletti Reference Truzzolillo and Cipelletti2017), which may be the case for droplet impact processes of a few milliseconds. Nevertheless, the measurements of interfacial tensions for water and glycerol mixtures show values of ![]() $1\ \textrm {mN}\ \textrm {m}^{-1}$ or lower (Petitjeans & Maxworthy Reference Petitjeans and Maxworthy1996), and approximately
$1\ \textrm {mN}\ \textrm {m}^{-1}$ or lower (Petitjeans & Maxworthy Reference Petitjeans and Maxworthy1996), and approximately ![]() $2\ \textrm {mN}\ \textrm {m}^{-1}$ for water and alcohols like butanol (Enders & Kahl Reference Enders and Kahl2008). These values remain within the experimental uncertainties, thus, the interfacial tension can be approximated to be zero for GW/EtOH.
$2\ \textrm {mN}\ \textrm {m}^{-1}$ for water and alcohols like butanol (Enders & Kahl Reference Enders and Kahl2008). These values remain within the experimental uncertainties, thus, the interfacial tension can be approximated to be zero for GW/EtOH.
In order to quantify the importance of the interfacial tension in the droplet/wall-film system, the non-dimensionalized interfacial tension ![]() $\sigma _{d/f}^{*}{}= \sigma _{d/f}{}/( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{})$ is introduced. It corresponds to the ratio of the interfacial tension to the sum of the surface tensions of droplet and wall film. Thus, it is zero for miscible liquids such as GW/EtOH, and increases with increasing importance of the interfacial tension in the droplet/wall-film system, as for GW/SO and GW/Hexa in the last row of table 1. Note that, in some cases, it could be interesting to have a unified parameter combining the importance of the interfacial tension with the spreading parameter, e.g. as
$\sigma _{d/f}^{*}{}= \sigma _{d/f}{}/( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{})$ is introduced. It corresponds to the ratio of the interfacial tension to the sum of the surface tensions of droplet and wall film. Thus, it is zero for miscible liquids such as GW/EtOH, and increases with increasing importance of the interfacial tension in the droplet/wall-film system, as for GW/SO and GW/Hexa in the last row of table 1. Note that, in some cases, it could be interesting to have a unified parameter combining the importance of the interfacial tension with the spreading parameter, e.g. as ![]() ${S^{*}}{}= \sigma _{d/f}{}/ S{}$ in the case where the spreading parameter is different from zero. This parameter could help to understand the kinetics of the receding where the wettability has a strong influence for example in the formation of a Worthington jet (Che & Matar Reference Che and Matar2018), whose magnitude could be related to
${S^{*}}{}= \sigma _{d/f}{}/ S{}$ in the case where the spreading parameter is different from zero. This parameter could help to understand the kinetics of the receding where the wettability has a strong influence for example in the formation of a Worthington jet (Che & Matar Reference Che and Matar2018), whose magnitude could be related to ![]() ${S^{*}}{}$. In the present study, we rather focus on the crown extension phase where the value of the interfacial tension seems to play a significant role independently of the wetting behaviour of the liquid pair, probably because of the large Weber numbers involved (see § 2.3).
${S^{*}}{}$. In the present study, we rather focus on the crown extension phase where the value of the interfacial tension seems to play a significant role independently of the wetting behaviour of the liquid pair, probably because of the large Weber numbers involved (see § 2.3).
2.3. Experimental range
The single droplets of the glycerol/water mixture exhibit diameters of ![]() ${D_{d}}{} = 2.20\pm 0.07\ \textrm {mm}$ for the full database. The impact velocity is varied from
${D_{d}}{} = 2.20\pm 0.07\ \textrm {mm}$ for the full database. The impact velocity is varied from ![]() ${V_{d}}{}=2.5$ to
${V_{d}}{}=2.5$ to ![]() $3.7\ \textrm {m}\ \textrm {s}^{-1}$ with four different fall heights. For each impact velocity investigated, all three liquid pairs are used as a wall film. The dimensionless wall-film thickness
$3.7\ \textrm {m}\ \textrm {s}^{-1}$ with four different fall heights. For each impact velocity investigated, all three liquid pairs are used as a wall film. The dimensionless wall-film thickness ![]() $\delta {}={h_{f}}{}/{D_{d}}{}$ is kept quasi-constant at two investigated ranges, i.e. at
$\delta {}={h_{f}}{}/{D_{d}}{}$ is kept quasi-constant at two investigated ranges, i.e. at ![]() $\delta =0.122\pm 0.011$, and at
$\delta =0.122\pm 0.011$, and at ![]() $\delta =0.259\pm 0.008$. In order to describe accurately the impact process, the initial state of the droplet/wall-film system needs to be quantified. Therefore, the range of Weber and Reynolds numbers based on droplet properties,
$\delta =0.259\pm 0.008$. In order to describe accurately the impact process, the initial state of the droplet/wall-film system needs to be quantified. Therefore, the range of Weber and Reynolds numbers based on droplet properties, ![]() $\mathit {We}_{d}{}= \rho _d {V_{d}}^{2} {D_{d}}{}/ \sigma _d$ and
$\mathit {We}_{d}{}= \rho _d {V_{d}}^{2} {D_{d}}{}/ \sigma _d$ and ![]() $\mathit {Re}_{d}=\rho_d {V_{d}}{}{D_{d}}{}/ \mu _d$ respectively, are given in the two first columns of table 2. Note that the range indicated includes the experimental conditions of all three liquids pairs of GW/Hexa, GW/SO and GW/EtOH. However, these numbers are not representative of the full binary droplet/wall-film systems since the liquid properties of droplet and wall film differ. A proper way of taking both droplet and wall-film liquid properties into account in these non-dimensional numbers is still under discussion in the literature (Geppert et al. Reference Geppert, Gomaa, Meister, Lamanna and Weigand2014; Kittel, Roisman & Tropea Reference Kittel, Roisman and Tropea2017). Recently, averaged liquid properties (subscript avg) such as
$\mathit {Re}_{d}=\rho_d {V_{d}}{}{D_{d}}{}/ \mu _d$ respectively, are given in the two first columns of table 2. Note that the range indicated includes the experimental conditions of all three liquids pairs of GW/Hexa, GW/SO and GW/EtOH. However, these numbers are not representative of the full binary droplet/wall-film systems since the liquid properties of droplet and wall film differ. A proper way of taking both droplet and wall-film liquid properties into account in these non-dimensional numbers is still under discussion in the literature (Geppert et al. Reference Geppert, Gomaa, Meister, Lamanna and Weigand2014; Kittel, Roisman & Tropea Reference Kittel, Roisman and Tropea2017). Recently, averaged liquid properties (subscript avg) such as ![]() $\rho _{avg}{}=( \rho _d{}+ \rho _f{})/2$,
$\rho _{avg}{}=( \rho _d{}+ \rho _f{})/2$, ![]() $\sigma _{avg}{}=( \sigma _d{}+ \sigma _f{})/2$ and
$\sigma _{avg}{}=( \sigma _d{}+ \sigma _f{})/2$ and ![]() $\nu _{avg}{}=\sqrt {{ \nu _d \nu _f}}$ have shown good ability to capture the crown rim dynamics for binary droplet/wall-film systems (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020). Note that this approach was developed for miscible droplet/wall-film liquid pairs made of silicone oils. Hence, it does not consider wettability and miscibility effects which are considered separately in the present study (e.g. in terms of spreading parameter
$\nu _{avg}{}=\sqrt {{ \nu _d \nu _f}}$ have shown good ability to capture the crown rim dynamics for binary droplet/wall-film systems (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020). Note that this approach was developed for miscible droplet/wall-film liquid pairs made of silicone oils. Hence, it does not consider wettability and miscibility effects which are considered separately in the present study (e.g. in terms of spreading parameter ![]() $S{}$ and dimensionless interfacial tension
$S{}$ and dimensionless interfacial tension ![]() $\sigma _{d/f}^{*}{}$ summarized in table 1). These averaged properties can be used in the dimensionless numbers to form
$\sigma _{d/f}^{*}{}$ summarized in table 1). These averaged properties can be used in the dimensionless numbers to form ![]() $\mathit {We}_{avg}{}$ and
$\mathit {We}_{avg}{}$ and ![]() $\mathit {Re}_{avg}{}$ summarized in table 2 for each reference value of
$\mathit {Re}_{avg}{}$ summarized in table 2 for each reference value of ![]() $\mathit {We}_{d}{}$ and all liquid pairs combined. Furthermore, they can be combined in a single impact parameter
$\mathit {We}_{d}{}$ and all liquid pairs combined. Furthermore, they can be combined in a single impact parameter ![]() $K{}= \mathit {We}^{0.5} \mathit {Re}^{0.25}$ (also summarized in the last column of table 2), which, considered together with
$K{}= \mathit {We}^{0.5} \mathit {Re}^{0.25}$ (also summarized in the last column of table 2), which, considered together with ![]() $\delta {}$, is fully representative of the droplet wall-film system for the onset of splashing (Cossali, Coghe & Marengo Reference Cossali, Coghe and Marengo1997). These non-dimensional impact parameters between the three liquid pairs indicate very similar droplet/wall-film systems for each set of experiments. The variation does not exceed
$\delta {}$, is fully representative of the droplet wall-film system for the onset of splashing (Cossali, Coghe & Marengo Reference Cossali, Coghe and Marengo1997). These non-dimensional impact parameters between the three liquid pairs indicate very similar droplet/wall-film systems for each set of experiments. The variation does not exceed ![]() ${\pm }8\,\%$ in general at a given
${\pm }8\,\%$ in general at a given ![]() $\mathit {We}_{d}{}$, while the non-dimensionalized interfacial tension
$\mathit {We}_{d}{}$, while the non-dimensionalized interfacial tension ![]() $\sigma _{d/f}^{*}{}$ increases by more than 25 % between GW/SO and GW/Hexa, and is zero for GW/EtOH. Hence, the major varying parameter between the liquid pairs investigated is
$\sigma _{d/f}^{*}{}$ increases by more than 25 % between GW/SO and GW/Hexa, and is zero for GW/EtOH. Hence, the major varying parameter between the liquid pairs investigated is ![]() $\sigma _{d/f}^{*}{}$, which, combined with the surface tensions of droplet and wall films, defines the miscibility and wettability of the liquid pairs.
$\sigma _{d/f}^{*}{}$, which, combined with the surface tensions of droplet and wall films, defines the miscibility and wettability of the liquid pairs.
Table 2. The investigation range of typical non-dimensional parameters. The subscript avg refers to averaged liquid properties between droplet and wall film.

3. Experimental observations
The temporal evolutions of the three liquid pairs are shown in figure 1. Despite similar impact conditions (see table 2, row ![]() $\delta {}= 0.130\pm 0.001$ with
$\delta {}= 0.130\pm 0.001$ with ![]() $\mathit {We}_{d}=363\pm 5$), differences between the liquid pairs can be observed in the impact outcome, the crown extension and the crown kinetics.
$\mathit {We}_{d}=363\pm 5$), differences between the liquid pairs can be observed in the impact outcome, the crown extension and the crown kinetics.
3.1. Shift in the splashing limit
The three droplet/wall-film pairs in figure 1 differ qualitatively in their impact outcomes. A movie in the supplementary material shows the temporal evolution of the impact process for each liquid pair side by side. For GW/Hexa, the crown rim stays relatively stable, undulations become significant only in the receding phase (the maximum crown height is reached at approximately ![]() $\tau _{in,H_{max}}{} = {t_{H_{max}}}{} {V_{d}}{}/{D_{d}}{} = 5.40$) and fingers can barely be observed at the end of the impact process. Thus, the outcome of GW/Hexa can be categorized as a transition case (i.e. fingers formed) close to deposition (i.e. no fingers). In the case of GW/SO, undulations on the rim already occur in the ascending phase (up to
$\tau _{in,H_{max}}{} = {t_{H_{max}}}{} {V_{d}}{}/{D_{d}}{} = 5.40$) and fingers can barely be observed at the end of the impact process. Thus, the outcome of GW/Hexa can be categorized as a transition case (i.e. fingers formed) close to deposition (i.e. no fingers). In the case of GW/SO, undulations on the rim already occur in the ascending phase (up to ![]() $\tau _{in,H_{max}}{} = 6.53$), and at the end of the extension process, long fingers with droplets about to detach are formed. The long fingers only disintegrate into secondary droplets at the end of the impact process, leaving the droplets in the vicinity of the impact location. Thus, the outcome of GW/SO can again be categorized as a transition case, but close to splashing (i.e. secondary droplets are ejected far off the crown).
$\tau _{in,H_{max}}{} = 6.53$), and at the end of the extension process, long fingers with droplets about to detach are formed. The long fingers only disintegrate into secondary droplets at the end of the impact process, leaving the droplets in the vicinity of the impact location. Thus, the outcome of GW/SO can again be categorized as a transition case, but close to splashing (i.e. secondary droplets are ejected far off the crown).
Note that the tiny droplets seen already at ![]() $\tau _{in}{} = 2.25$ are associated with prompt splashing, i.e. they are not considered as part of the crown-type outcome. The prompt splashing consists in the fragmentation of a thin and fast liquid lamella called ejecta sheet (Thoroddsen Reference Thoroddsen2002) formed at the base of the impacting droplet. The distinction between prompt and crown-type splashing relies first on their different time scales, since prompt splashing occurs quasi-immediately after the droplet impact onto the liquid surface (within the first
$\tau _{in}{} = 2.25$ are associated with prompt splashing, i.e. they are not considered as part of the crown-type outcome. The prompt splashing consists in the fragmentation of a thin and fast liquid lamella called ejecta sheet (Thoroddsen Reference Thoroddsen2002) formed at the base of the impacting droplet. The distinction between prompt and crown-type splashing relies first on their different time scales, since prompt splashing occurs quasi-immediately after the droplet impact onto the liquid surface (within the first ![]() $100\ \mathrm {\mu } \textrm {s}$, Liang & Mudawar (Reference Liang and Mudawar2016)). Second, the ejecta sheet and the crown wall arise from a different dynamics and can be observed distinctly (Zhang et al. Reference Zhang, Toole, Fezzaa and Deegan2012). Third, prompt and crown-type splashing can be observed independently of each other in a splashing regime map (Deegan, Brunet & Eggers Reference Deegan, Brunet and Eggers2007). Last, prompt splashing forms much smaller secondary droplets than crown-type splashing (Cossali et al. Reference Cossali, Coghe and Marengo1997; Motzkus, Gensdarmes & Géhin Reference Motzkus, Gensdarmes and Géhin2009). Hence, there is most likely no or small interdependence between the prompt splashing observed and the crown-type splashing studied in the present experiments. The movie of the impact experiments, similar to those of figure 1 in the supplementary material shows prompt splashing in all three cases upon droplet penetration into the wall film, although the tiny droplets produced are ejected beyond the crown size and thus observable later only for GW/SO and GW/EtOH.
$100\ \mathrm {\mu } \textrm {s}$, Liang & Mudawar (Reference Liang and Mudawar2016)). Second, the ejecta sheet and the crown wall arise from a different dynamics and can be observed distinctly (Zhang et al. Reference Zhang, Toole, Fezzaa and Deegan2012). Third, prompt and crown-type splashing can be observed independently of each other in a splashing regime map (Deegan, Brunet & Eggers Reference Deegan, Brunet and Eggers2007). Last, prompt splashing forms much smaller secondary droplets than crown-type splashing (Cossali et al. Reference Cossali, Coghe and Marengo1997; Motzkus, Gensdarmes & Géhin Reference Motzkus, Gensdarmes and Géhin2009). Hence, there is most likely no or small interdependence between the prompt splashing observed and the crown-type splashing studied in the present experiments. The movie of the impact experiments, similar to those of figure 1 in the supplementary material shows prompt splashing in all three cases upon droplet penetration into the wall film, although the tiny droplets produced are ejected beyond the crown size and thus observable later only for GW/SO and GW/EtOH.
For the last liquid pair GW/EtOH, fingers are already formed in the ascending phase (e.g. at ![]() $\tau _{in}{} = 4.50$), and some droplets are ejected from the fingers. Towards the end of the crown extension, holes are formed on the crown wall, as known from droplet impacts with aqueous and ethanol solutions (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2006; Aljedaani et al. Reference Aljedaani, Wang, Jetly and Thoroddsen2018). As explained in the introduction, mixture composition gradients in the crown wall and/or fine droplets which cannot be observed with the current set-up impacting on the crown wall could cause these holes.
$\tau _{in}{} = 4.50$), and some droplets are ejected from the fingers. Towards the end of the crown extension, holes are formed on the crown wall, as known from droplet impacts with aqueous and ethanol solutions (Thoroddsen et al. Reference Thoroddsen, Etoh and Takehara2006; Aljedaani et al. Reference Aljedaani, Wang, Jetly and Thoroddsen2018). As explained in the introduction, mixture composition gradients in the crown wall and/or fine droplets which cannot be observed with the current set-up impacting on the crown wall could cause these holes.
Despite the formation of holes in the crown (the first occurrence could be back tracked at ![]() $\tau _{in}{} = 6.30$), it is seen that a few, bigger secondary droplets are ejected from the fingers. Thus, the outcome of GW/EtOH can be categorized as a splashing case close to transition, since only few droplets are ejected. Hence, a small shift in the splashing limit is observed between the three cases despite similar liquid properties and impact conditions: the miscible pair GW/EtOH starts to splash, the full wetting pair GW/SO is close to splash and the partially wetting pair GW/Hexa is closer to deposition. Note that the smallest viscosity (despite the small differences between the pairs) is that of n-hexadecane. Since less viscous losses are expected, splashing with less kinetic energy should be observed (see the review article of Liang & Mudawar (Reference Liang and Mudawar2016)). Since this is not the case, small viscosity variations are not expected to modify the trend observed between the liquid pairs. This shift in the fragmentation limit, classically derived based on empirical observation of the outcome, is very small. Thus, it is hard to evaluate it in terms of the critical Weber or Reynolds number. Furthermore, there is a smooth transition from deposition to splashing (Cossali et al. Reference Cossali, Coghe and Marengo1997), so that the transition outcome (Geppert et al. Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016) is used to refine the splashing criteria. However, qualitatively, the averaged Weber number
$\tau _{in}{} = 6.30$), it is seen that a few, bigger secondary droplets are ejected from the fingers. Thus, the outcome of GW/EtOH can be categorized as a splashing case close to transition, since only few droplets are ejected. Hence, a small shift in the splashing limit is observed between the three cases despite similar liquid properties and impact conditions: the miscible pair GW/EtOH starts to splash, the full wetting pair GW/SO is close to splash and the partially wetting pair GW/Hexa is closer to deposition. Note that the smallest viscosity (despite the small differences between the pairs) is that of n-hexadecane. Since less viscous losses are expected, splashing with less kinetic energy should be observed (see the review article of Liang & Mudawar (Reference Liang and Mudawar2016)). Since this is not the case, small viscosity variations are not expected to modify the trend observed between the liquid pairs. This shift in the fragmentation limit, classically derived based on empirical observation of the outcome, is very small. Thus, it is hard to evaluate it in terms of the critical Weber or Reynolds number. Furthermore, there is a smooth transition from deposition to splashing (Cossali et al. Reference Cossali, Coghe and Marengo1997), so that the transition outcome (Geppert et al. Reference Geppert, Chatzianagnostou, Mesiter, Gomaa, Lamanna and Weigand2016) is used to refine the splashing criteria. However, qualitatively, the averaged Weber number ![]() $\mathit {We}_{avg}{}$ defined in § 2 could be modified taking into account all surface and interfacial tensions with
$\mathit {We}_{avg}{}$ defined in § 2 could be modified taking into account all surface and interfacial tensions with ![]() $( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{})/3$ instead of
$( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{})/3$ instead of ![]() $( \sigma _d{}+ \sigma _f{})/2$. This would lead to a characteristic Weber number of the impact multiplied by 0.98 for GW/Hexa, 1.08 for GW/SO and 1.5 for GW/EtOH, highlighting that GW/EtOH would cross the splashing limit earlier than GW/SO and finally than GW/Hexa. This difficulty to assert the splashing limit for such a narrow difference highlights the need to consider another parameter to quantify the differences observed between the liquid pairs.
$( \sigma _d{}+ \sigma _f{})/2$. This would lead to a characteristic Weber number of the impact multiplied by 0.98 for GW/Hexa, 1.08 for GW/SO and 1.5 for GW/EtOH, highlighting that GW/EtOH would cross the splashing limit earlier than GW/SO and finally than GW/Hexa. This difficulty to assert the splashing limit for such a narrow difference highlights the need to consider another parameter to quantify the differences observed between the liquid pairs.
3.2. Shift in crown extension
In addition to the small shift in the fragmentation observed in figure 1, the liquid pairs show differences in the size of the crown. To quantify this observation, the crown surface is calculated from the high-speed images by extracting the geometrical parameters of the crown as shown in the schematic of figure 2. The crown rim height ![]() ${H_{R}}{}$, the rim radius
${H_{R}}{}$, the rim radius ![]() ${R_{R}}{}$ and the base radius
${R_{R}}{}$ and the base radius ![]() ${R_{B}}{}$ are extracted from the crown edges marked with orange circles. The crown surface, expressed as
${R_{B}}{}$ are extracted from the crown edges marked with orange circles. The crown surface, expressed as
is calculated by summing the surface of the disc at the crown base, and the surface of the crown wall counted twice for the inner and outer parts. The crown wall is approximated by a conical frustum formed between the base and rim radii. This assumes having a straight line between the base and rim radii, although sometimes the crown wall is slightly bent inward. This bending and its influence on the determination of the crown surface is discussed in appendix B. However, the difference in crown morphologies (between the crown edges) is taken indirectly into account via the calculation of ![]() $\varSigma _{c}{}$. In addition, the surface area at the rim due to the crown thickness is neglected.
$\varSigma _{c}{}$. In addition, the surface area at the rim due to the crown thickness is neglected.
The propagation of uncertainty from the measurements of ![]() ${H_{R}}{}$,
${H_{R}}{}$, ![]() ${R_{R}}{}$ and
${R_{R}}{}$ and ![]() ${R_{B}}{}$ (given in § 2.1) to
${R_{B}}{}$ (given in § 2.1) to ![]() $\varSigma _{c}{}$ can be calculated based on the formula of Gauss–Laplace. The corresponding relative measurement uncertainty is dependent upon the crown morphology, i.e.
$\varSigma _{c}{}$ can be calculated based on the formula of Gauss–Laplace. The corresponding relative measurement uncertainty is dependent upon the crown morphology, i.e. ![]() ${H_{R}}{}/{R_{R}}{}$ and
${H_{R}}{}/{R_{R}}{}$ and ![]() ${R_{B}}{}/{R_{R}}{}$. Note that these ratios vary during the impact process, and between different impact conditions. The typical crown configuration in the present experimental conditions (
${R_{B}}{}/{R_{R}}{}$. Note that these ratios vary during the impact process, and between different impact conditions. The typical crown configuration in the present experimental conditions (![]() ${H_{R}}{}/{R_{R}}{} \approx {} 0.5$ and
${H_{R}}{}/{R_{R}}{} \approx {} 0.5$ and ![]() ${R_{B}}{}/{R_{R}}{} \approx {} 1$) leads to an error of 5.7 %, while the extreme crown aspect ratios (
${R_{B}}{}/{R_{R}}{} \approx {} 1$) leads to an error of 5.7 %, while the extreme crown aspect ratios (![]() ${H_{R}}{}/{R_{R}}{}$ from 0.05 to 0.65, and
${H_{R}}{}/{R_{R}}{}$ from 0.05 to 0.65, and ![]() ${R_{B}}{}/{R_{R}}{}$ from 0.65 to 1.30) lead to errors of up to 8.27 %, tendentially for high
${R_{B}}{}/{R_{R}}{}$ from 0.65 to 1.30) lead to errors of up to 8.27 %, tendentially for high ![]() ${R_{B}}{}$ and/or small
${R_{B}}{}$ and/or small ![]() ${H_{R}}{}$.
${H_{R}}{}$.
The temporal evolution of ![]() $\varSigma _{c}{}$ is shown in figure 3(a) for the same experiments as in figure 1 that have similar impact conditions. Except at the early stage of impact, where kinetic energy dominates, the curves separate progressively. As observed qualitatively in the high-speed images, the crown surface of GW/Hexa is smaller than that of GW/SO, which is smaller than that of GW/EtOH. Note that this ranking of crown surface extensions correlates with the values of
$\varSigma _{c}{}$ is shown in figure 3(a) for the same experiments as in figure 1 that have similar impact conditions. Except at the early stage of impact, where kinetic energy dominates, the curves separate progressively. As observed qualitatively in the high-speed images, the crown surface of GW/Hexa is smaller than that of GW/SO, which is smaller than that of GW/EtOH. Note that this ranking of crown surface extensions correlates with the values of ![]() $\sigma _{d/f}^{*}{}$ reported in table 1: The larger is
$\sigma _{d/f}^{*}{}$ reported in table 1: The larger is ![]() $\sigma _{d/f}^{*}{}$ (tendentially for immiscible liquid pairs with partial wetting), the smaller becomes the crown surface. A similar ranking in the spreading between miscible and immiscible droplet/wall films during the crown extension phase has also been measured by Chen et al. (Reference Chen, Chen and Amirfazli2017), without being explained. The formation of holes in the crown of GW/EtOH (grey symbols in figure 3) does not influence this trend since the values of
$\sigma _{d/f}^{*}{}$ (tendentially for immiscible liquid pairs with partial wetting), the smaller becomes the crown surface. A similar ranking in the spreading between miscible and immiscible droplet/wall films during the crown extension phase has also been measured by Chen et al. (Reference Chen, Chen and Amirfazli2017), without being explained. The formation of holes in the crown of GW/EtOH (grey symbols in figure 3) does not influence this trend since the values of ![]() $\varSigma _{c}{}$ for GW/EtOH are systematically above, but adds noise which prevents the exact determination of the maximum crown surface
$\varSigma _{c}{}$ for GW/EtOH are systematically above, but adds noise which prevents the exact determination of the maximum crown surface ![]() $\varSigma _{c,max}{}$ (filled symbols in figure 3a,b);
$\varSigma _{c,max}{}$ (filled symbols in figure 3a,b); ![]() $\varSigma _{c,max}{}$ for GW/EtOH is lying between the value where the first hole appears (filled grey symbols and grey dashed line), and the maximum value calculated before the destruction of the crown (filled red symbols and red dashed line). Furthermore, the determination of the crown parameters during extension remains repeatable despite stochastic holes (Geppert et al. Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017).
$\varSigma _{c,max}{}$ for GW/EtOH is lying between the value where the first hole appears (filled grey symbols and grey dashed line), and the maximum value calculated before the destruction of the crown (filled red symbols and red dashed line). Furthermore, the determination of the crown parameters during extension remains repeatable despite stochastic holes (Geppert et al. Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017).
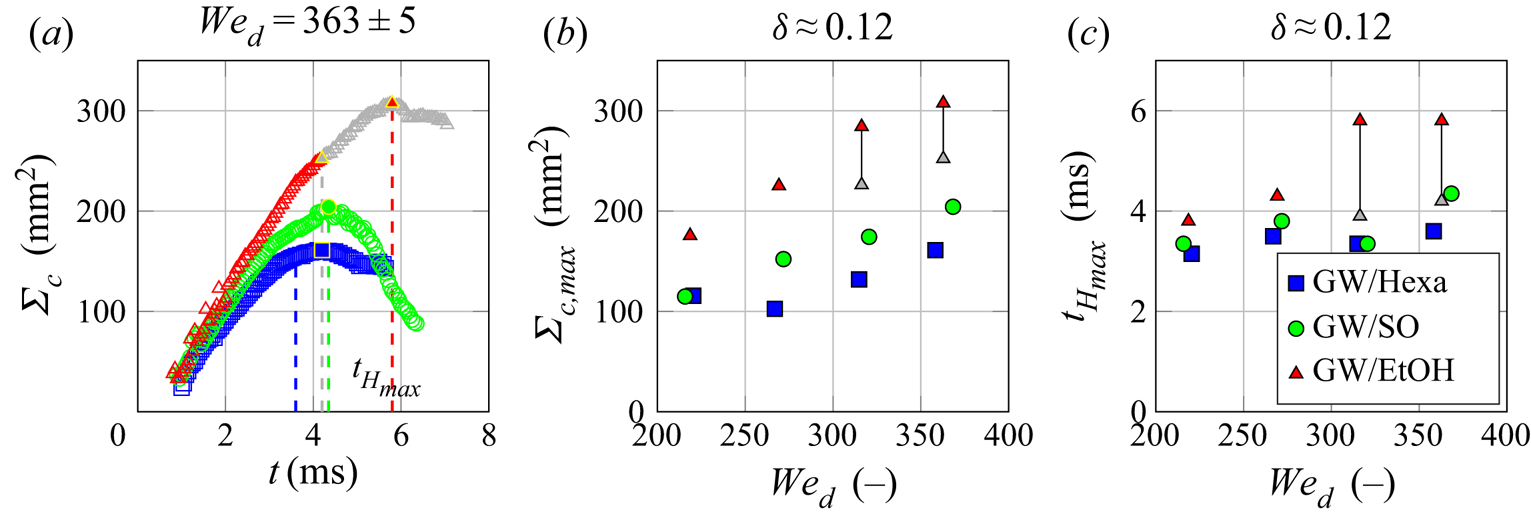
Figure 3. (a) Temporal evolution of the crown surface ![]() $\varSigma _{c}{}$ for the same experiments as in figure 1. The filled symbols with yellow edge correspond to
$\varSigma _{c}{}$ for the same experiments as in figure 1. The filled symbols with yellow edge correspond to ![]() $\varSigma _{c,max}{}$. The dashed lines correspond to
$\varSigma _{c,max}{}$. The dashed lines correspond to ![]() ${t_{H_{max}}}{}$, the time at which
${t_{H_{max}}}{}$, the time at which ![]() ${H_{R,max}}{}$ is reached. (b) Maximum crown surface
${H_{R,max}}{}$ is reached. (b) Maximum crown surface ![]() $\varSigma _{c,max}{}$ at different Weber numbers
$\varSigma _{c,max}{}$ at different Weber numbers ![]() $\mathit {We}_{d}{}$. (c) Time duration
$\mathit {We}_{d}{}$. (c) Time duration ![]() ${t_{H_{max}}}{}$ of the crown ascending phase (marked with dashed lines in (a)) at different Weber numbers
${t_{H_{max}}}{}$ of the crown ascending phase (marked with dashed lines in (a)) at different Weber numbers ![]() $\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant for the data of this figure at
$\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant for the data of this figure at ![]() $\delta =0.122\pm 0.011$. The grey symbols correspond to the measurements where holes in the crown are observed (only for GW/EtOH).
$\delta =0.122\pm 0.011$. The grey symbols correspond to the measurements where holes in the crown are observed (only for GW/EtOH).
The values of ![]() $\varSigma _{c,max}{}$ are reported for different Weber numbers in figure 3(b). It is clear that the trend observed between the liquid pairs in (a) remains the same: at a given
$\varSigma _{c,max}{}$ are reported for different Weber numbers in figure 3(b). It is clear that the trend observed between the liquid pairs in (a) remains the same: at a given ![]() $\mathit {We}_{d}{}$, the values of
$\mathit {We}_{d}{}$, the values of ![]() $\varSigma _{c,max}{}$ are systematically smaller for GW/Hexa than for GW/SO, which are smaller than GW/EtOH. For a given liquid pair,
$\varSigma _{c,max}{}$ are systematically smaller for GW/Hexa than for GW/SO, which are smaller than GW/EtOH. For a given liquid pair, ![]() $\varSigma _{c,max}{}$ increases with growing
$\varSigma _{c,max}{}$ increases with growing ![]() $\mathit {We}_{d}{}$, i.e. with increasing droplet kinetic energy. This corroborates the larger rim expansions observed at higher droplet kinetic energy for droplet impacts onto wall films (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020), or for other impact configurations, e.g. onto dry surfaces (Huang & Chen Reference Huang and Chen2018), with another droplet (Roisman et al. Reference Roisman, Planchette, Lorenceau and Brenn2012) or with a continuous jet (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
$\mathit {We}_{d}{}$, i.e. with increasing droplet kinetic energy. This corroborates the larger rim expansions observed at higher droplet kinetic energy for droplet impacts onto wall films (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020), or for other impact configurations, e.g. onto dry surfaces (Huang & Chen Reference Huang and Chen2018), with another droplet (Roisman et al. Reference Roisman, Planchette, Lorenceau and Brenn2012) or with a continuous jet (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
3.3. Shift in duration of crown ascending phase
It is interesting to note that the duration of the crown ascending phase (i.e. the time at which ![]() ${H_{R,max}}{}$ is reached, marked by dashed lines in figure 3a) also exhibits a systematic ranking between the liquid pairs, although of smaller amplitude than the differences in crown surfaces. The ascending duration of GW/Hexa is smaller than that of GW/SO, which may be smaller than that of GW/EtOH (the grey dashed line corresponds to the time at which the first hole could be back tracked). Here again, this ranking correlates with the values of
${H_{R,max}}{}$ is reached, marked by dashed lines in figure 3a) also exhibits a systematic ranking between the liquid pairs, although of smaller amplitude than the differences in crown surfaces. The ascending duration of GW/Hexa is smaller than that of GW/SO, which may be smaller than that of GW/EtOH (the grey dashed line corresponds to the time at which the first hole could be back tracked). Here again, this ranking correlates with the values of ![]() $\sigma _{d/f}^{*}{}$ reported in table 1. The higher is
$\sigma _{d/f}^{*}{}$ reported in table 1. The higher is ![]() $\sigma _{d/f}^{*}{}$, the shorter becomes the ascending duration.
$\sigma _{d/f}^{*}{}$, the shorter becomes the ascending duration.
Note that a similar observation could not be made with ![]() ${t_{\varSigma _{c,max}}}{}$ (the time at which the maximum crown surface is reached). In fact, the exact time of crown surface receding is unclear because it has, in some cases, a plateau at its maximum value. This effect is known as the stabilization phase of the crown at the end of the surface extension (Zhang et al. Reference Zhang, Liu, Qu and Hu2019). This happens when the radial extension of the crown is longer than the axial one (Bernard et al. Reference Bernard, Geppert, Vaikuntanathan, Lamanna and Weigand2018). In this case, the decrease of
${t_{\varSigma _{c,max}}}{}$ (the time at which the maximum crown surface is reached). In fact, the exact time of crown surface receding is unclear because it has, in some cases, a plateau at its maximum value. This effect is known as the stabilization phase of the crown at the end of the surface extension (Zhang et al. Reference Zhang, Liu, Qu and Hu2019). This happens when the radial extension of the crown is longer than the axial one (Bernard et al. Reference Bernard, Geppert, Vaikuntanathan, Lamanna and Weigand2018). In this case, the decrease of ![]() ${H_{R}}{}$ is compensated by a continuous increase of
${H_{R}}{}$ is compensated by a continuous increase of ![]() ${R_{R}}{}$ and/or
${R_{R}}{}$ and/or ![]() ${R_{B}}{}$. This effect shifts
${R_{B}}{}$. This effect shifts ![]() ${t_{\varSigma _{c,max}}}{}$ compared with
${t_{\varSigma _{c,max}}}{}$ compared with ![]() ${t_{H_{max}}}{}$ (as in figure 3a for GW/Hexa between the blue filled symbol and the blue dashed line) and leads to scattered data. Hence,
${t_{H_{max}}}{}$ (as in figure 3a for GW/Hexa between the blue filled symbol and the blue dashed line) and leads to scattered data. Hence, ![]() ${t_{H_{max}}}{}$ is preferred to
${t_{H_{max}}}{}$ is preferred to ![]() ${t_{\varSigma _{c,max}}}{}$. The durations of the crown ascending phase
${t_{\varSigma _{c,max}}}{}$. The durations of the crown ascending phase ![]() ${t_{H_{max}}}{}$ are given in figure 3(c) for different
${t_{H_{max}}}{}$ are given in figure 3(c) for different ![]() $\mathit {We}_{d}{}$. A trend between the liquid pairs is observed, similar to the maximum crown surface
$\mathit {We}_{d}{}$. A trend between the liquid pairs is observed, similar to the maximum crown surface ![]() $\varSigma _{c,max}{}$: the ascending phase of GW/Hexa is slightly shorter than that of GW/SO, which is (not systematically) slightly smaller than GW/EtOH. These durations are slightly increasing with growing
$\varSigma _{c,max}{}$: the ascending phase of GW/Hexa is slightly shorter than that of GW/SO, which is (not systematically) slightly smaller than GW/EtOH. These durations are slightly increasing with growing ![]() $\mathit {We}_{d}{}$, as already observed for example with droplet impacts onto dry surfaces (Huang & Chen Reference Huang and Chen2018), but not for droplet head-on collisions or impacts onto a continuous jet, where the kinetics is fixed by the encapsulated drop only (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
$\mathit {We}_{d}{}$, as already observed for example with droplet impacts onto dry surfaces (Huang & Chen Reference Huang and Chen2018), but not for droplet head-on collisions or impacts onto a continuous jet, where the kinetics is fixed by the encapsulated drop only (Baumgartner et al. Reference Baumgartner, Bernard, Weigand, Lamanna, Brenn and Planchette2020).
In summary, slight differences between the liquid pairs were observed for the onset of splashing, but more prominently, differences in maximum crown surface and in the duration of the crown ascending phase despite similar impact conditions and liquid properties were measured. Thus, these differences can be attributed to their wettability and miscibility behaviours.
4. Importance of the interfacial tension
The miscibility and wettability behaviours responsible for the differences observed in § 3 are linked to the interfacial tension ![]() $\sigma _{d/f}^{*}{}$ characteristic of each liquid droplet/wall-film pair (see table 1). During droplet impact onto thin wall films, the initial kinetic energy of the droplet is partially converted into surface energy and partially dissipated due to impact losses (initial droplet deformation) and viscous losses during the extension phase. This energy transfer leads to an important crown extension and a significant role of the surface forces. Although the role of surface tension is quite clear, the importance of interfacial tension for droplet impact onto wall films during extension remains poorly documented and understood. In the following, we investigate the role of the interfacial tension, starting with energetical considerations followed by kinetic ones.
$\sigma _{d/f}^{*}{}$ characteristic of each liquid droplet/wall-film pair (see table 1). During droplet impact onto thin wall films, the initial kinetic energy of the droplet is partially converted into surface energy and partially dissipated due to impact losses (initial droplet deformation) and viscous losses during the extension phase. This energy transfer leads to an important crown extension and a significant role of the surface forces. Although the role of surface tension is quite clear, the importance of interfacial tension for droplet impact onto wall films during extension remains poorly documented and understood. In the following, we investigate the role of the interfacial tension, starting with energetical considerations followed by kinetic ones.
4.1. Energy storage
In order to estimate if the differences in the crown extension observed in § 3.2 can be explained by the differences in interfacial tension ![]() $\sigma _{d/f}$, the temporal evolution of the crown surface energy
$\sigma _{d/f}$, the temporal evolution of the crown surface energy ![]() ${E_{\sigma ,c}}{}$ is calculated. Each portion of the crown (i.e. base disc and conical frustum) is multiplied by the corresponding surface/interfacial tension (i.e.
${E_{\sigma ,c}}{}$ is calculated. Each portion of the crown (i.e. base disc and conical frustum) is multiplied by the corresponding surface/interfacial tension (i.e. ![]() $\sigma _d$,
$\sigma _d$, ![]() $\sigma _f$ and/or
$\sigma _f$ and/or ![]() $\sigma _{d/f}$). The droplet liquid is assumed to completely cover the wall-film liquid on the inside of the crown, as represented in figure 2. This full coverage by the droplet liquid on the inner crown wall has been observed numerically for aqueous droplet/wall-film systems (Zhang et al. Reference Zhang, Liu, Qu and Hu2019), and experimentally for dyed water droplet impacting onto silicone oil films (Shaikh et al. Reference Shaikh, Toyofuku, Hoang and Marston2018), for
$\sigma _{d/f}$). The droplet liquid is assumed to completely cover the wall-film liquid on the inside of the crown, as represented in figure 2. This full coverage by the droplet liquid on the inner crown wall has been observed numerically for aqueous droplet/wall-film systems (Zhang et al. Reference Zhang, Liu, Qu and Hu2019), and experimentally for dyed water droplet impacting onto silicone oil films (Shaikh et al. Reference Shaikh, Toyofuku, Hoang and Marston2018), for ![]() $Re_{f}=\rho _{f}{V_{d}}{}{h_{f}}/\mu _{f}$ below 400 (Kittel et al. Reference Kittel, Roisman and Tropea2018a). In the current work, the maximum value of
$Re_{f}=\rho _{f}{V_{d}}{}{h_{f}}/\mu _{f}$ below 400 (Kittel et al. Reference Kittel, Roisman and Tropea2018a). In the current work, the maximum value of ![]() $\mathit {Re}_{f}{}$ is 196. Hence, it can reasonably be assumed that the droplet liquid completely covers the inner part of the crown, which leads to the following expression for the crown surface energy:
$\mathit {Re}_{f}{}$ is 196. Hence, it can reasonably be assumed that the droplet liquid completely covers the inner part of the crown, which leads to the following expression for the crown surface energy:
The propagation of uncertainty for ![]() ${E_{\sigma ,c}}{}$ can be calculated similar to that of the crown surface
${E_{\sigma ,c}}{}$ can be calculated similar to that of the crown surface ![]() $\varSigma _{c}{}$, by considering additionally the measurement uncertainty associated with the surface and interfacial tensions given in table 1. This provides a propagation of error for the reference geometrical configuration (
$\varSigma _{c}{}$, by considering additionally the measurement uncertainty associated with the surface and interfacial tensions given in table 1. This provides a propagation of error for the reference geometrical configuration (![]() ${H_{R}}{}/{R_{R}}{} \approx {} 0.5$ and
${H_{R}}{}/{R_{R}}{} \approx {} 0.5$ and ![]() ${R_{B}}{}/{R_{R}}{}\approx {} 1$) of 6.1 % for GW/Hexa, 7.2 % for GW/SO and 7.6 % for GW/EtOH. By considering the extreme values of the crown geometrical configuration, the maximum propagation of uncertainty to
${R_{B}}{}/{R_{R}}{}\approx {} 1$) of 6.1 % for GW/Hexa, 7.2 % for GW/SO and 7.6 % for GW/EtOH. By considering the extreme values of the crown geometrical configuration, the maximum propagation of uncertainty to ![]() ${E_{\sigma ,c}}{}$ becomes 9.6 % (obtained for GW/EtOH).
${E_{\sigma ,c}}{}$ becomes 9.6 % (obtained for GW/EtOH).
The temporal evolution of ![]() ${E_{\sigma ,c}}{}$ is shown in figure 4(a) for the same cases as in figure 3(a). In contrast to
${E_{\sigma ,c}}{}$ is shown in figure 4(a) for the same cases as in figure 3(a). In contrast to ![]() $\varSigma _{c}{}$, the maxima are now comparable (note that at a constant Weber number,
$\varSigma _{c}{}$, the maxima are now comparable (note that at a constant Weber number, ![]() ${E_{k,d,0}}{}$ is constant for the three liquid pairs). Indeed, the overall surface energy of GW/Hexa, which has the smallest crown surface, is relatively increased due to the high value of
${E_{k,d,0}}{}$ is constant for the three liquid pairs). Indeed, the overall surface energy of GW/Hexa, which has the smallest crown surface, is relatively increased due to the high value of ![]() $\sigma _{d/f}$ for this liquid pair. Likewise, the overall surface energy of GW/EtOH, which has the biggest crown surface, is relatively decreased since the interfacial tension is zero (miscible liquid pair). In between lies the case of GW/SO. For all
$\sigma _{d/f}$ for this liquid pair. Likewise, the overall surface energy of GW/EtOH, which has the biggest crown surface, is relatively decreased since the interfacial tension is zero (miscible liquid pair). In between lies the case of GW/SO. For all ![]() $\mathit {We}_{d}{}$ investigated in our study, all
$\mathit {We}_{d}{}$ investigated in our study, all ![]() ${E_{\sigma ,c,max}}{}$ normalized with the droplet kinetic energy
${E_{\sigma ,c,max}}{}$ normalized with the droplet kinetic energy ![]() ${E_{k,d,0}}{}=\rho _d {\rm \pi}{D_{d}}^{3} {V_{d}}^{2}/12$ are systematically coming together. Hence, the interfacial tension appears as a good candidate to explain the differences in maximum crown extensions. This means that, for immiscible liquid pairs, the interface between droplet and wall film stores a non-negligible amount of energy during the extension phase, proportionally to
${E_{k,d,0}}{}=\rho _d {\rm \pi}{D_{d}}^{3} {V_{d}}^{2}/12$ are systematically coming together. Hence, the interfacial tension appears as a good candidate to explain the differences in maximum crown extensions. This means that, for immiscible liquid pairs, the interface between droplet and wall film stores a non-negligible amount of energy during the extension phase, proportionally to ![]() $\sigma _{d/f}^{*}{}$. This stored energy neither participates in the crown extension, nor in the splashing process. Hence, liquid pairs with smaller interfacial tension (the limit being zero for miscible cases) expand more, and splash tendentially at lower droplet kinetic energy, as observed in figure 1. For impact processes with smaller extensions (e.g. at very small
$\sigma _{d/f}^{*}{}$. This stored energy neither participates in the crown extension, nor in the splashing process. Hence, liquid pairs with smaller interfacial tension (the limit being zero for miscible cases) expand more, and splash tendentially at lower droplet kinetic energy, as observed in figure 1. For impact processes with smaller extensions (e.g. at very small ![]() $\mathit {We}_{d}{}$, or onto another impacted substrates), the interfacial energy could be less significant and its effect may not be noticeable.
$\mathit {We}_{d}{}$, or onto another impacted substrates), the interfacial energy could be less significant and its effect may not be noticeable.
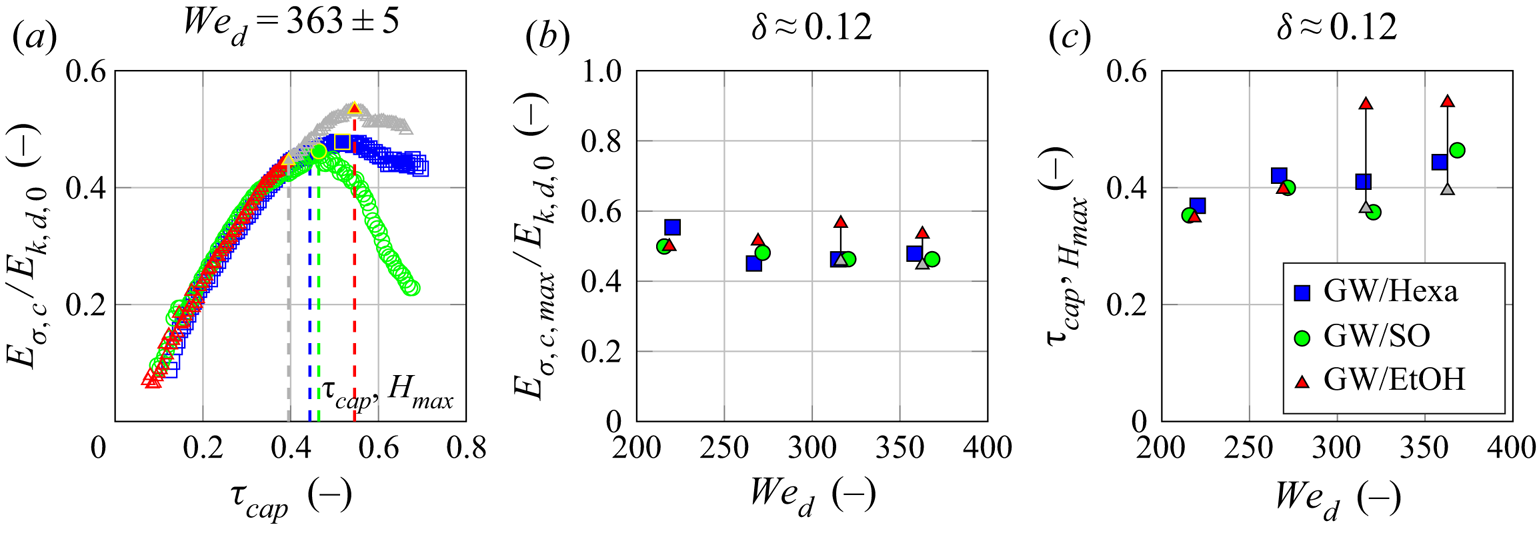
Figure 4. (a) Temporal evolution of the crown surface energy ![]() ${E_{\sigma ,c}}{}$ normalized with the initial droplet kinetic energy
${E_{\sigma ,c}}{}$ normalized with the initial droplet kinetic energy ![]() ${E_{k,d,0}}{}$ as a function of
${E_{k,d,0}}{}$ as a function of ![]() $\tau _{cap}{}$ (see (4.2)) for the same experiments as in figures 1 and 3(a). The filled symbols with yellow edge correspond to
$\tau _{cap}{}$ (see (4.2)) for the same experiments as in figures 1 and 3(a). The filled symbols with yellow edge correspond to ![]() ${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$. The dashed lines correspond to
${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$. The dashed lines correspond to ![]() $\tau _{cap,H_{max}}{}$, the time at which
$\tau _{cap,H_{max}}{}$, the time at which ![]() ${H_{R,max}}{}$ is reached normalized with
${H_{R,max}}{}$ is reached normalized with ![]() ${t_{cap}}{}$. (b) Maximum crown surface energy
${t_{cap}}{}$. (b) Maximum crown surface energy ![]() ${E_{\sigma ,c,max}}{}$ normalized with the initial droplet kinetic energy
${E_{\sigma ,c,max}}{}$ normalized with the initial droplet kinetic energy ![]() ${E_{k,d,0}}{}$ at different Weber numbers
${E_{k,d,0}}{}$ at different Weber numbers ![]() $\mathit {We}_{d}{}$. (c) Capillary time duration
$\mathit {We}_{d}{}$. (c) Capillary time duration ![]() $\tau _{cap,H_{max}}{}$ of the crown ascending phase (highlighted with dashed lines in (a)) at different Weber numbers
$\tau _{cap,H_{max}}{}$ of the crown ascending phase (highlighted with dashed lines in (a)) at different Weber numbers ![]() $\mathit {We}_{d}{}$. The capillary time scale
$\mathit {We}_{d}{}$. The capillary time scale ![]() ${t_{cap}}{}$ used has a typical spring constant of
${t_{cap}}{}$ used has a typical spring constant of ![]() $\sigma _d{}+ \sigma _{d/f}{}+ \sigma _f{}$ and a characteristic mass
$\sigma _d{}+ \sigma _{d/f}{}+ \sigma _f{}$ and a characteristic mass ![]() ${M_d}{}+{M_f}{}=( \rho _d+ \rho _f ) {\rm \pi}{D_{d}}^{3}/6$. The dimensionless wall-film thickness is kept constant for the data of this figure at
${M_d}{}+{M_f}{}=( \rho _d+ \rho _f ) {\rm \pi}{D_{d}}^{3}/6$. The dimensionless wall-film thickness is kept constant for the data of this figure at ![]() $\delta =0.122\pm 0.011$. The grey symbols correspond to the measurements where holes in the crown are observed (only for GW/EtOH).
$\delta =0.122\pm 0.011$. The grey symbols correspond to the measurements where holes in the crown are observed (only for GW/EtOH).
The ratio of ![]() ${E_{\sigma ,c,max}}{}$ with
${E_{\sigma ,c,max}}{}$ with ![]() ${E_{k,d,0}}{}$ in figure 4(b) indicates how much the incoming kinetic energy has been transferred into surface energy. On average, this ratio is approximately 50 % of the initial kinetic energy in our experimental range. This amount corroborates numerical simulations at similar
${E_{k,d,0}}{}$ in figure 4(b) indicates how much the incoming kinetic energy has been transferred into surface energy. On average, this ratio is approximately 50 % of the initial kinetic energy in our experimental range. This amount corroborates numerical simulations at similar ![]() $\mathit {We}_{d}{}$ and wall-film thickness of aqueous droplet/wall-film systems (Zhang et al. Reference Zhang, Liu, Qu and Hu2019). Similar values have also been found in numerical simulations of droplet impacts onto dry surfaces with slip condition (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016), i.e. with negligible surface friction which can be likened to a liquid interface.
$\mathit {We}_{d}{}$ and wall-film thickness of aqueous droplet/wall-film systems (Zhang et al. Reference Zhang, Liu, Qu and Hu2019). Similar values have also been found in numerical simulations of droplet impacts onto dry surfaces with slip condition (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016), i.e. with negligible surface friction which can be likened to a liquid interface.
At the end of crown extension, the quantity ![]() $1-{E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ is representative of the remaining energy and losses before the onset of retraction. Some kinetic energy might remain due to internal flow motions and the complex shape of the crown. Furthermore, the motion of a liquid mass in the vertical direction leads to a conversion of kinetic energy into gravitational energy. Numerical studies of water droplet impacts onto wall films at
$1-{E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ is representative of the remaining energy and losses before the onset of retraction. Some kinetic energy might remain due to internal flow motions and the complex shape of the crown. Furthermore, the motion of a liquid mass in the vertical direction leads to a conversion of kinetic energy into gravitational energy. Numerical studies of water droplet impacts onto wall films at ![]() $\delta {}=0.1$ and
$\delta {}=0.1$ and ![]() $\mathit {We}_{d}{}=250$ (Zhang et al. Reference Zhang, Liu, Qu and Hu2019) show that, at the end of the expansion, the remaining kinetic energy is approximately 8 % of
$\mathit {We}_{d}{}=250$ (Zhang et al. Reference Zhang, Liu, Qu and Hu2019) show that, at the end of the expansion, the remaining kinetic energy is approximately 8 % of ![]() ${E_{k,d,0}}{}$, and the gravitational energy 2 %. Combined with a surface energy of approximately 50 %, this corresponds to an energy loss of approximately 40 % of the droplet kinetic energy during the extension phase. This corroborates the study on dry surfaces with slip condition at the wall (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016), where they found 10 % remaining energy (no gravitational energy since the spreading is horizontal), and 40 % of
${E_{k,d,0}}{}$, and the gravitational energy 2 %. Combined with a surface energy of approximately 50 %, this corresponds to an energy loss of approximately 40 % of the droplet kinetic energy during the extension phase. This corroborates the study on dry surfaces with slip condition at the wall (Wildeman et al. Reference Wildeman, Visser, Sun and Lohse2016), where they found 10 % remaining energy (no gravitational energy since the spreading is horizontal), and 40 % of ![]() ${E_{k,d,0}}{}$ converted into heat. Hence, in the present droplet/wall-film experiments, the remaining kinetic and gravitational energies at the end of crown extension are expected to be approximately 10 % of
${E_{k,d,0}}{}$ converted into heat. Hence, in the present droplet/wall-film experiments, the remaining kinetic and gravitational energies at the end of crown extension are expected to be approximately 10 % of ![]() ${E_{k,d,0}}{}$. Note that the gravitational energy is thus minor for
${E_{k,d,0}}{}$. Note that the gravitational energy is thus minor for ![]() $\delta {}=0.1$, but for a higher wall-film thickness, such as
$\delta {}=0.1$, but for a higher wall-film thickness, such as ![]() $\delta {}=0.3$, it can represent up to 15 % of the crown surface energy (Cossali et al. Reference Cossali, Marengo, Coghe and Zhdanov2004).
$\delta {}=0.3$, it can represent up to 15 % of the crown surface energy (Cossali et al. Reference Cossali, Marengo, Coghe and Zhdanov2004).
A full energy balance of the impact process (always assuming a zero kinetic energy at maximum crown surface) should also consider the initial surface energies of droplet and wall film. The initial surface energy of the droplet can be calculated with ![]() ${E_{\sigma ,d,0}}={\rm \pi} {D_{d}}^{2} \sigma _{d}$. For the wall film, the initial surface energy can be approximated with the free surface of the wall film covered by the crown base at maximum extension, i.e.
${E_{\sigma ,d,0}}={\rm \pi} {D_{d}}^{2} \sigma _{d}$. For the wall film, the initial surface energy can be approximated with the free surface of the wall film covered by the crown base at maximum extension, i.e. ![]() ${E_{\sigma ,f,0}}\approx {\rm \pi}R^{2}_{{B,max}} \sigma _{f}$ (see e.g. similar approaches for droplet impact onto dry surfaces by Vaikuntanathan & Sivakumar (Reference Vaikuntanathan and Sivakumar2016)). This surface corresponds to the free surface of the wall film covered by the crown base at maximum extension and is therefore an impact-dependent variable that can be estimated a posteriori in the present database. The values of
${E_{\sigma ,f,0}}\approx {\rm \pi}R^{2}_{{B,max}} \sigma _{f}$ (see e.g. similar approaches for droplet impact onto dry surfaces by Vaikuntanathan & Sivakumar (Reference Vaikuntanathan and Sivakumar2016)). This surface corresponds to the free surface of the wall film covered by the crown base at maximum extension and is therefore an impact-dependent variable that can be estimated a posteriori in the present database. The values of ![]() ${E_{\sigma ,c,max}}{}/({E_{k,d,0}}+{E_{\sigma ,d,0}}+{E_{\sigma ,f,0}})$ taking all initial energies into account would be diminished from 5 % to 10 % compared with
${E_{\sigma ,c,max}}{}/({E_{k,d,0}}+{E_{\sigma ,d,0}}+{E_{\sigma ,f,0}})$ taking all initial energies into account would be diminished from 5 % to 10 % compared with ![]() ${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ alone given in figure 4(b). Since this shift roughly corresponds to the value of the remaining kinetic and gravitational energies of approximately 10 % of
${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ alone given in figure 4(b). Since this shift roughly corresponds to the value of the remaining kinetic and gravitational energies of approximately 10 % of ![]() ${E_{k,d,0}}{}$ at the end of the crown extension discussed previously, this means that
${E_{k,d,0}}{}$ at the end of the crown extension discussed previously, this means that ![]() ${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ gives an estimation of the losses at the end of the crown extension, of approximately 50 % of all initial energies for these impact conditions.
${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ gives an estimation of the losses at the end of the crown extension, of approximately 50 % of all initial energies for these impact conditions.
Looking at the influence of the droplet kinetic energy, the maximum crown surface energy normalized with the droplet kinetic energy slightly decreases with increasing ![]() $\mathit {We}_{d}{}$. Hence, the percentage of total losses is increasing with growing
$\mathit {We}_{d}{}$. Hence, the percentage of total losses is increasing with growing ![]() $\mathit {We}_{d}{}$, which can be explained by higher deformation losses of the impacting droplet (Gao & Li Reference Gao and Li2015) and a more pronounced influence of the boundary layer because of a higher shear due to the higher velocity gradient, and a deeper penetration of the droplet bringing the flow closer to the wall (Lamanna, Geppert & Weigand Reference Lamanna, Geppert and Weigand2019).
$\mathit {We}_{d}{}$, which can be explained by higher deformation losses of the impacting droplet (Gao & Li Reference Gao and Li2015) and a more pronounced influence of the boundary layer because of a higher shear due to the higher velocity gradient, and a deeper penetration of the droplet bringing the flow closer to the wall (Lamanna, Geppert & Weigand Reference Lamanna, Geppert and Weigand2019).
The extension of the experimental database to ![]() $\delta {} \approx {} 0.26$ given in appendix B shows a similar data reduction of the normalized crown surface energies between the different liquid pairs at a given Weber number. However, the values are now higher compared with
$\delta {} \approx {} 0.26$ given in appendix B shows a similar data reduction of the normalized crown surface energies between the different liquid pairs at a given Weber number. However, the values are now higher compared with ![]() $\delta {} \approx {} 0.12$, of approximately 0.6 and above. This corroborates the influence of shear during the extension process since it is expected to be reduced for higher wall-film thickness because of a decreased influence of the solid wall. However, a more refined quantitative analysis is not possible here since the potential energies and remaining kinetic energy at the end of crown extension might be larger for a wall-film thickness above 0.2 (Zhang et al. Reference Zhang, Liu, Qu and Hu2019).
$\delta {} \approx {} 0.12$, of approximately 0.6 and above. This corroborates the influence of shear during the extension process since it is expected to be reduced for higher wall-film thickness because of a decreased influence of the solid wall. However, a more refined quantitative analysis is not possible here since the potential energies and remaining kinetic energy at the end of crown extension might be larger for a wall-film thickness above 0.2 (Zhang et al. Reference Zhang, Liu, Qu and Hu2019).
To conclude, the interface (if any) between the droplet and wall film stores a non-negligible amount of energy during the extension. Taking into account the interfacial energy generalizes the estimation of viscous losses made for miscible liquid pairs to immiscible ones with different interfacial tensions. With approximately 50 % loss of the initial surface and kinetic energies for ![]() $\delta {} \approx {} 0.1$, the viscous effects prevent the crown extension as much as the capillary forces for thin wall films. Hence, the droplet/wall-film system should be considered as an inertio-capillary-viscous system.
$\delta {} \approx {} 0.1$, the viscous effects prevent the crown extension as much as the capillary forces for thin wall films. Hence, the droplet/wall-film system should be considered as an inertio-capillary-viscous system.
4.2. Recoiling force
Droplet impact processes can be considered as oscillating mass–spring systems (Okumura et al. Reference Okumura, Chevy, Richard, Quéré and Clanet2003; Planchette et al. Reference Planchette, Hinterbichler, Liu, Bothe and Brenn2017), where surface tension is the recoiling force opposing the deformation induced by the impacting droplet. Hence, the droplet and the wall film could be seen as springs in parallel whose spring constants are given by the surface and interfacial tensions. Following this reasoning, the system during impact could be represented by an equivalent spring constant equal to the sum of each, i.e. ![]() $\sigma _d+\sigma _f+\sigma _{d/f}$. Considering the crown as an inertio-capillary system, the capillary time scales of the crown ascending phase (i.e. increase of
$\sigma _d+\sigma _f+\sigma _{d/f}$. Considering the crown as an inertio-capillary system, the capillary time scales of the crown ascending phase (i.e. increase of ![]() ${H_{R}}{}$) can be compared for the three liquid pairs to see whether the trend between the liquid pairs observed in figure 3(c) is related to the differences in interfacial tensions. Thus, we propose to evaluate the capillary time based on the equivalent spring constant as
${H_{R}}{}$) can be compared for the three liquid pairs to see whether the trend between the liquid pairs observed in figure 3(c) is related to the differences in interfacial tensions. Thus, we propose to evaluate the capillary time based on the equivalent spring constant as
 \begin{equation} \tau_{cap}{}=\frac{t}{{t_{cap}}{}}=\frac{t}{\sqrt{\dfrac{{M_d}{}+{M_f}{}}{\sigma_d+\sigma_{d/f}+\sigma_f}}}. \end{equation}
\begin{equation} \tau_{cap}{}=\frac{t}{{t_{cap}}{}}=\frac{t}{\sqrt{\dfrac{{M_d}{}+{M_f}{}}{\sigma_d+\sigma_{d/f}+\sigma_f}}}. \end{equation} The characteristic mass of the droplet/wall-film system entering ![]() ${t_{cap}}{}$ is most likely a combination of droplet and wall-film masses as (
${t_{cap}}{}$ is most likely a combination of droplet and wall-film masses as (![]() ${M_d}{}+{M_f}{}$). While the characteristic mass of the droplet can be easily calculated before impact as
${M_d}{}+{M_f}{}$). While the characteristic mass of the droplet can be easily calculated before impact as ![]() ${{M_d}{}}={ \rho _d} {\rm \pi}{D_{d}}^{3}/6$, the determination of wall-film mass
${{M_d}{}}={ \rho _d} {\rm \pi}{D_{d}}^{3}/6$, the determination of wall-film mass ![]() ${M_f}{}$ is more difficult. By assuming an equal volume of droplet and wall-film liquid participating in the oscillation process, we get
${M_f}{}$ is more difficult. By assuming an equal volume of droplet and wall-film liquid participating in the oscillation process, we get ![]() ${{M_d}{}}+{{M_f}{}}=({ \rho _d}+{ \rho _f} ) {\rm \pi}{D_{d}}^{3}/6$. This rough estimation has the advantage of being determined with pre-impact parameters. In figure 4(a), the time is non-dimensionalized with
${{M_d}{}}+{{M_f}{}}=({ \rho _d}+{ \rho _f} ) {\rm \pi}{D_{d}}^{3}/6$. This rough estimation has the advantage of being determined with pre-impact parameters. In figure 4(a), the time is non-dimensionalized with ![]() ${t_{cap}}{}$ to form
${t_{cap}}{}$ to form ![]() $\tau _{cap}{}$. Compared with
$\tau _{cap}{}$. Compared with ![]() ${t_{H_{max}}}{}$ in figure 3(a), we observe that
${t_{H_{max}}}{}$ in figure 3(a), we observe that ![]() $\tau _{cap,H_{max}}{}$ (the non-dimensional time at which
$\tau _{cap,H_{max}}{}$ (the non-dimensional time at which ![]() ${H_{R,max}}{}$ is reached) are coming together. Indeed, the differences of
${H_{R,max}}{}$ is reached) are coming together. Indeed, the differences of ![]() $\sigma _{d/f}{}$ in
$\sigma _{d/f}{}$ in ![]() ${t_{cap}}{}$ compensate the differences in extension duration for each liquid pair, similar to the compensating effect for
${t_{cap}}{}$ compensate the differences in extension duration for each liquid pair, similar to the compensating effect for ![]() ${E_{\sigma ,c,max}}{}$ in figure 4(b). Hence, the interfacial tension is responsible for the different durations of ascending phases.
${E_{\sigma ,c,max}}{}$ in figure 4(b). Hence, the interfacial tension is responsible for the different durations of ascending phases.
This means that, for immiscible liquid pairs, the interface between droplet and wall film acts as a non-negligible force preventing the extension, proportionally to ![]() $\sigma _{d/f}^{*}{}$. This scaling leads to a unified temporal evolution for the three liquid pairs of the normalized crown surface energy with the capillary time during the ascending phase at a given impact condition. The role of interfacial tension is observed for all impact conditions investigated in our study as shown in figure 4(c), all data points coming together at a given
$\sigma _{d/f}^{*}{}$. This scaling leads to a unified temporal evolution for the three liquid pairs of the normalized crown surface energy with the capillary time during the ascending phase at a given impact condition. The role of interfacial tension is observed for all impact conditions investigated in our study as shown in figure 4(c), all data points coming together at a given ![]() $\mathit {We}_{d}{}$;
$\mathit {We}_{d}{}$; ![]() $\tau _{cap,H_{max}}{}$ is approximately 0.4, similar to what has been also observed for much lower Weber numbers (below 10) for the droplet oscillation alone impacting a shallow and deep pool (Tang et al. Reference Tang, Saha, Sun and Law2019).
$\tau _{cap,H_{max}}{}$ is approximately 0.4, similar to what has been also observed for much lower Weber numbers (below 10) for the droplet oscillation alone impacting a shallow and deep pool (Tang et al. Reference Tang, Saha, Sun and Law2019).
The values of ![]() $\tau _{cap,H_{max}}{}$ are slightly increasing with increasing
$\tau _{cap,H_{max}}{}$ are slightly increasing with increasing ![]() $\mathit {We}_{d}{}$. This indicates that
$\mathit {We}_{d}{}$. This indicates that ![]() $\tau _{cap}{}$ cannot properly capture the process for all impact conditions, but only highlights the influence of the interfacial tension during the extension. The consideration of the inertial time
$\tau _{cap}{}$ cannot properly capture the process for all impact conditions, but only highlights the influence of the interfacial tension during the extension. The consideration of the inertial time ![]() $\tau _{in,H_{max}}{}={t_{H_{max}}}{}{V_{d}}{}/{D_{d}}{}$ would lead to an even stronger dependency on the Weber number since
$\tau _{in,H_{max}}{}={t_{H_{max}}}{}{V_{d}}{}/{D_{d}}{}$ would lead to an even stronger dependency on the Weber number since ![]() $\mathit {We}_{d}{}$ increases with
$\mathit {We}_{d}{}$ increases with ![]() ${V_{d}}{}$. Furthermore, it would not bring the experiments together at a given
${V_{d}}{}$. Furthermore, it would not bring the experiments together at a given ![]() $\mathit {We}_{d}{}$ since no surface tensions are considered. A viscous time as
$\mathit {We}_{d}{}$ since no surface tensions are considered. A viscous time as ![]() ${D_{d}}^{2}/\nu$ would also let the ranking of
${D_{d}}^{2}/\nu$ would also let the ranking of ![]() ${t_{H_{max}}}{}$ and the trend with
${t_{H_{max}}}{}$ and the trend with ![]() $\mathit {We}_{d}{}$ unchanged given the similar kinematic viscosities involved for all impact conditions (see table 1).
$\mathit {We}_{d}{}$ unchanged given the similar kinematic viscosities involved for all impact conditions (see table 1).
The extension of the experimental database to ![]() ${\delta {}} \approx {} 0.26$ represented in figure 5 shows a similar data reduction of the ascending phase durations between the different liquid pairs at a given Weber number. However, the values are now higher compared with
${\delta {}} \approx {} 0.26$ represented in figure 5 shows a similar data reduction of the ascending phase durations between the different liquid pairs at a given Weber number. However, the values are now higher compared with ![]() ${\delta {}} \approx {} 0.12$, lying around 0.6. Furthermore, the trend with increasing Weber number becomes weaker compared with
${\delta {}} \approx {} 0.12$, lying around 0.6. Furthermore, the trend with increasing Weber number becomes weaker compared with ![]() ${\delta {}} \approx {} 0.12$, exhibiting almost constant values.
${\delta {}} \approx {} 0.12$, exhibiting almost constant values.
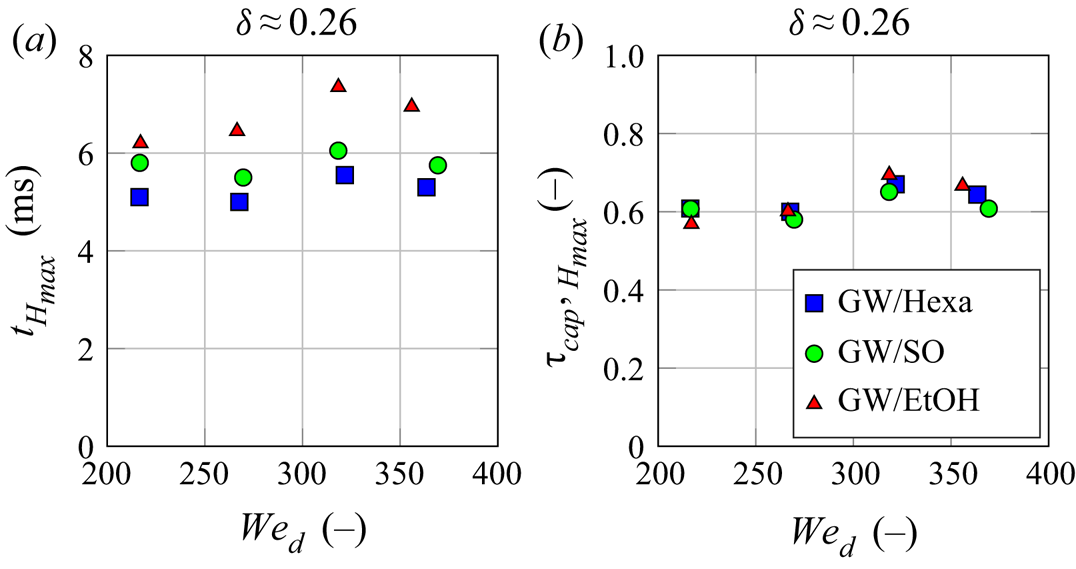
Figure 5. (a) Time duration ![]() ${t_{H_{max}}}{}$ of the crown ascending phase at different Weber numbers
${t_{H_{max}}}{}$ of the crown ascending phase at different Weber numbers ![]() $\mathit {We}_{d}{}$. (b) Capillary time duration
$\mathit {We}_{d}{}$. (b) Capillary time duration ![]() $\tau _{cap,H_{max}}{}$ of the crown ascending phase at different Weber numbers
$\tau _{cap,H_{max}}{}$ of the crown ascending phase at different Weber numbers ![]() $\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant at
$\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant at ![]() ${\delta }=0.259\pm 0.008$ for the data of this figure.
${\delta }=0.259\pm 0.008$ for the data of this figure.
The discrepancies in oscillation periods between different Weber numbers and wall-film thicknesses suggest that the scaling coefficient ![]() ${t_{cap}}{}$ defined above does not capture the full complexity of the impact process, especially regarding the role of inertia and damping effects. In the following, reasons for these discrepancies are proposed, focusing on the role of the interacting mass during the crown extension, of the viscous damping, and of an altered isochronism of oscillations.
${t_{cap}}{}$ defined above does not capture the full complexity of the impact process, especially regarding the role of inertia and damping effects. In the following, reasons for these discrepancies are proposed, focusing on the role of the interacting mass during the crown extension, of the viscous damping, and of an altered isochronism of oscillations.
First, the characteristic mass used in ![]() ${t_{cap}}{}$ is very likely dependent upon the impact conditions. Indeed, the kinetic energy of the droplet influences the droplet penetration inside the film. This could lead to an increased interacting wall-film mass, which is not captured with the current capillary scaling assuming an equal amount of droplet and wall-film liquids. Similarly, larger wall-film thicknesses increase the available amount of wall-film liquid that could enter the crown. Hence, the estimation of the interacting mass of wall film needs to be refined to get a deeper insight into the oscillating behaviour. Therefore, the maximal interacting wall-film mass
${t_{cap}}{}$ is very likely dependent upon the impact conditions. Indeed, the kinetic energy of the droplet influences the droplet penetration inside the film. This could lead to an increased interacting wall-film mass, which is not captured with the current capillary scaling assuming an equal amount of droplet and wall-film liquids. Similarly, larger wall-film thicknesses increase the available amount of wall-film liquid that could enter the crown. Hence, the estimation of the interacting mass of wall film needs to be refined to get a deeper insight into the oscillating behaviour. Therefore, the maximal interacting wall-film mass ![]() ${M_f}{}$ can be estimated by considering the mass contained in a cylinder of radius
${M_f}{}$ can be estimated by considering the mass contained in a cylinder of radius ![]() ${R_{B}}{}$ at
${R_{B}}{}$ at ![]() ${t_{H_{max}}}{}$ and of height equal to the difference of the wall-film height
${t_{H_{max}}}{}$ and of height equal to the difference of the wall-film height ![]() ${h_{f}}{}$ with the residual film thickness
${h_{f}}{}$ with the residual film thickness ![]() ${h_{res}}{}$, as
${h_{res}}{}$, as ![]() ${{M_f}{}}= { \rho _f{}} {\rm \pi}{R_{B}}^{2}({{t_{H_{max}}}{}}) ({{h_{f}}{}} - {{h_{res}}{}})$. The residual thickness corresponds to the thickness of the wall film which is not set in motion by the droplet impact. It can be approximated with
${{M_f}{}}= { \rho _f{}} {\rm \pi}{R_{B}}^{2}({{t_{H_{max}}}{}}) ({{h_{f}}{}} - {{h_{res}}{}})$. The residual thickness corresponds to the thickness of the wall film which is not set in motion by the droplet impact. It can be approximated with ![]() ${{h_{res}}{}} \approx (0.098{\delta {}}^{4.0413}+0.79){ \mathit {Re}}^{-2/5} {{D_{d}}{}}$ (van Hinsberg et al. Reference van Hinsberg, Budakli, Göhler, Berberović, Roisman, Gambaryan-Roisman, Tropea and Stephan2010). Hence, the residual thickness increases with increasing initial wall-film thickness, and decreases with increasing Reynolds number due to a deeper penetration of the droplet in the wall film.
${{h_{res}}{}} \approx (0.098{\delta {}}^{4.0413}+0.79){ \mathit {Re}}^{-2/5} {{D_{d}}{}}$ (van Hinsberg et al. Reference van Hinsberg, Budakli, Göhler, Berberović, Roisman, Gambaryan-Roisman, Tropea and Stephan2010). Hence, the residual thickness increases with increasing initial wall-film thickness, and decreases with increasing Reynolds number due to a deeper penetration of the droplet in the wall film.
In the present database, the Reynolds number can be approximated with averaged liquid properties as introduced in § 2.3 on the experimental range, corresponding to ![]() $\mathit {Re}_{avg}$. For the value of
$\mathit {Re}_{avg}$. For the value of ![]() ${{R_{B}}{}}({{t_{H_{max}}}{}})$, it has now the drawback that it should be extracted post-impact. For predicting purposes, however, one could use available theoretical models predicting
${{R_{B}}{}}({{t_{H_{max}}}{}})$, it has now the drawback that it should be extracted post-impact. For predicting purposes, however, one could use available theoretical models predicting ![]() ${R_{B}}{}$ in the literature, e.g. that of Roisman, van Hinsberg & Tropea (Reference Roisman, van Hinsberg and Tropea2008) predicting the maximum value of
${R_{B}}{}$ in the literature, e.g. that of Roisman, van Hinsberg & Tropea (Reference Roisman, van Hinsberg and Tropea2008) predicting the maximum value of ![]() ${R_{B}}{}$ during the impact process in function of
${R_{B}}{}$ during the impact process in function of ![]() $\mathit {We}_{d}{}$,
$\mathit {We}_{d}{}$, ![]() $\delta {}$ and the Froude number
$\delta {}$ and the Froude number ![]() $\mathit {Fr}_{d}{}$.
$\mathit {Fr}_{d}{}$.
The experimental data scaled with the modified capillary time scale ![]() $\tau _{cap,H_{max},m}{}$ based on the maximum mass of the wall film are given in figure 6 for
$\tau _{cap,H_{max},m}{}$ based on the maximum mass of the wall film are given in figure 6 for ![]() ${\delta {}} \approx {} 0.12$ (a) and
${\delta {}} \approx {} 0.12$ (a) and ![]() ${\delta {}} \approx {} 0.26$ (b). It can be seen that the values are now comparable for both wall-film thicknesses. Hence, the modified scaling captures the oscillating dynamics for different wall-film thicknesses, due to the increase of the characteristic mass. This correction also enables us to reduce the dependency with
${\delta {}} \approx {} 0.26$ (b). It can be seen that the values are now comparable for both wall-film thicknesses. Hence, the modified scaling captures the oscillating dynamics for different wall-film thicknesses, due to the increase of the characteristic mass. This correction also enables us to reduce the dependency with ![]() $\mathit {We}_{d}{}$ for
$\mathit {We}_{d}{}$ for ![]() ${\delta {}} \approx {} 0.1$. Yet, a slight slow down of the crown dynamics with increasing
${\delta {}} \approx {} 0.1$. Yet, a slight slow down of the crown dynamics with increasing ![]() $\mathit {We}_{d}{}$ can still be observed. Hence, additional effects might be responsible for this remaining trend.
$\mathit {We}_{d}{}$ can still be observed. Hence, additional effects might be responsible for this remaining trend.
Figure 6. (a) Time duration ![]() ${t_{H_{max}}}{}$ of the crown ascending phase at different Weber numbers
${t_{H_{max}}}{}$ of the crown ascending phase at different Weber numbers ![]() $\mathit {We}_{d}{}$. (b) Capillary time duration
$\mathit {We}_{d}{}$. (b) Capillary time duration ![]() $\tau _{cap,H_{max}}{}$ of the crown ascending phase at different Weber numbers
$\tau _{cap,H_{max}}{}$ of the crown ascending phase at different Weber numbers ![]() $\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant at
$\mathit {We}_{d}{}$. The dimensionless wall-film thickness is kept constant at ![]() $\delta =0.259\pm 0.008$ for the entire database.
$\delta =0.259\pm 0.008$ for the entire database.
Considering a classical oscillating mass–spring system, the damping can increase the inviscid oscillating period ![]() ${t_{cap}}{}$ as
${t_{cap}}{}$ as ![]() ${{t_{cap,\nu }}{}} = 2 {\rm \pi}/ ({\omega _{cap}}\sqrt {1-{\eta }^{2}})$, where
${{t_{cap,\nu }}{}} = 2 {\rm \pi}/ ({\omega _{cap}}\sqrt {1-{\eta }^{2}})$, where ![]() $\omega _{cap}{}$ is the inviscid pulsation and
$\omega _{cap}{}$ is the inviscid pulsation and ![]() $\eta {}$ the damping ratio. Applied to oscillating droplets during an impact, the damping ratio can be expressed as
$\eta {}$ the damping ratio. Applied to oscillating droplets during an impact, the damping ratio can be expressed as ![]() ${\eta {}} \approx {} 32\nu {{t_{cap}}{}}/(2{\rm \pi} {D_{d}}^{2})$ by approximating a damping coefficient of
${\eta {}} \approx {} 32\nu {{t_{cap}}{}}/(2{\rm \pi} {D_{d}}^{2})$ by approximating a damping coefficient of ![]() $32\nu /{D_{d}}^{2}$ (Tang et al. Reference Tang, Saha, Sun and Law2019). By replacing
$32\nu /{D_{d}}^{2}$ (Tang et al. Reference Tang, Saha, Sun and Law2019). By replacing ![]() ${t_{cap}}{}$ in
${t_{cap}}{}$ in ![]() $\eta {}$, the damping ratio can be re-expressed with the impact parameters of the present study in terms of a modified Ohnesorge number as
$\eta {}$, the damping ratio can be re-expressed with the impact parameters of the present study in terms of a modified Ohnesorge number as ![]() $\eta {}=16{\rm \pi} { \textit {Oh}}/9$, with
$\eta {}=16{\rm \pi} { \textit {Oh}}/9$, with ![]() $\textit {Oh}=\nu {}\sqrt {({ \rho _d{}}+{ \rho _f{}})/(2{D_{d}}{}( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{}))}$. The maximum value of Oh in the present database (considering averaged kinematic viscosity as
$\textit {Oh}=\nu {}\sqrt {({ \rho _d{}}+{ \rho _f{}})/(2{D_{d}}{}( \sigma _d{}+ \sigma _f{}+ \sigma _{d/f}{}))}$. The maximum value of Oh in the present database (considering averaged kinematic viscosity as ![]() $\sqrt { \nu _d \nu _f}$ suitable for binary droplet/wall-film system (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020)) is less than 0.015, leading to
$\sqrt { \nu _d \nu _f}$ suitable for binary droplet/wall-film system (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020)) is less than 0.015, leading to ![]() $\eta {}=0.084$, and an increase of
$\eta {}=0.084$, and an increase of ![]() ${t_{cap}}{}$ of less than 0.5 %. Hence, the damping due to viscosity alone is negligible. Note, however, that this damping does not take shear into account during the extension, which has been shown to play a significant role in the crown extension dynamics at the base (Geppert et al. Reference Geppert, Bernard, Weigand and Lamanna2020) and at the rim (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020). This viscous losses due to shear might increase the damping, and with it the oscillation period when shear increases. Since shear losses are expected to increase with increasing
${t_{cap}}{}$ of less than 0.5 %. Hence, the damping due to viscosity alone is negligible. Note, however, that this damping does not take shear into account during the extension, which has been shown to play a significant role in the crown extension dynamics at the base (Geppert et al. Reference Geppert, Bernard, Weigand and Lamanna2020) and at the rim (Bernard et al. Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020). This viscous losses due to shear might increase the damping, and with it the oscillation period when shear increases. Since shear losses are expected to increase with increasing ![]() $\mathit {We}_{d}{}$, as highlighted by the increasing trend of
$\mathit {We}_{d}{}$, as highlighted by the increasing trend of ![]() $1-{{E_{\sigma ,c,max}}{}}/{{E_{k,d,0}}{}}$ in figure 4(b), this could explain the increasing trend of
$1-{{E_{\sigma ,c,max}}{}}/{{E_{k,d,0}}{}}$ in figure 4(b), this could explain the increasing trend of ![]() $\tau _{cap,H_{max}}{}$ with growing
$\tau _{cap,H_{max}}{}$ with growing ![]() $\mathit {We}_{d}{}$. This also corroborates that this trend is weaker for
$\mathit {We}_{d}{}$. This also corroborates that this trend is weaker for ![]() $\delta {}=0.2$ where shear is smaller because the influence of the solid wall is reduced.
$\delta {}=0.2$ where shear is smaller because the influence of the solid wall is reduced.
Another mechanism that could lead to the increase of ![]() $\tau _{cap,H_{max}}{}$ with growing
$\tau _{cap,H_{max}}{}$ with growing ![]() $\mathit {We}_{d}{}$ is the amplitude of the oscillation. Since droplet/wall-film systems are characterized by large extensions, the isochronism of small oscillations might be altered. In this case, the oscillation period increases with increasing amplitude (Fulcher & Davis Reference Fulcher and Davis1976) which corresponds in our case to the Weber number.
$\mathit {We}_{d}{}$ is the amplitude of the oscillation. Since droplet/wall-film systems are characterized by large extensions, the isochronism of small oscillations might be altered. In this case, the oscillation period increases with increasing amplitude (Fulcher & Davis Reference Fulcher and Davis1976) which corresponds in our case to the Weber number.
To conclude, the interface (if any) between the droplet and wall film brings a supplementary recoiling force during the extension. Similar to a mass–spring oscillating system, the interfacial tension influences the oscillation behaviour of immiscible droplet/wall-film systems. Furthermore, the impact configuration (especially the wall-film thickness and the droplet kinetic energy) changes the characteristic mass of the system by modifying the mass of wall film interacting in the crown, and the influence of shear, which might influence the damping significantly.
5. Conclusions
The influence of miscibility and wettability in terms of spreading parameter is investigated for droplet impact onto thin wall films: immiscible with partial wetting, with full wetting or miscible. At similar liquid properties, this corresponds to a variation of the interfacial tension between the droplet and the wall film. First, shifts in the splashing limit as well as in the crown extensions are observed. Lower interfacial tension tendentially promotes splashing and larger crown extensions. These discrepancies vanish by taking into account the energy stored in the interface (if any) between the droplet and the wall film. An energy balance at the end of crown extension taking into account all surface and interfacial tensions also highlights that almost half of the initial kinetic energy is lost for thin wall films. Second, a shift in the duration of the crown ascending phase is observed. Smaller interfacial tensions result in longer durations. These differences vanish by scaling time with a capillary time scale taking into account both surface and interfacial tensions, indicating an inertio-capillary-driven system. The dynamics is well captured by the capillary time for different wall-film thicknesses if accounting for the variations of the liquid masses in movement. Shear at the crown base during extension might also prolong the crown ascending phase by influencing the damping rate. To conclude, the interfacial tension leads to a non-negligible energy storage and recoiling force for droplet impact onto thin wall films where the extension is important. The interfacial tension, which is linked to miscibility and wettability, needs to be taken into account to understand the impact dynamics and to model it accurately.
Acknowledgements
The authors gratefully acknowledge the financial support by the Deutsche Forschungsgemeinschaft (DFG) within the international research training group GRK2160/1 Droplet Interaction Technologies (DROPIT) in the frame of the Summer School 2018.
Declaration of interests
The authors report no conflict of interest.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2020.944.
Appendix A. Schematic of the experimental set-up and description of the image analysis
The high-speed images obtained with the experimental set-up shown in figure 7 are first processed by subtracting the background image (first image before the droplet enters the frame). This step, combined with an increase of contrast (grey scale spread over the full dynamic range), improves significantly the observation of the liquid structures. Thus, the processed high-speed images, as shown in figure 1, are preferred to the raw images (as in appendix B for example) to illustrate the impact process.
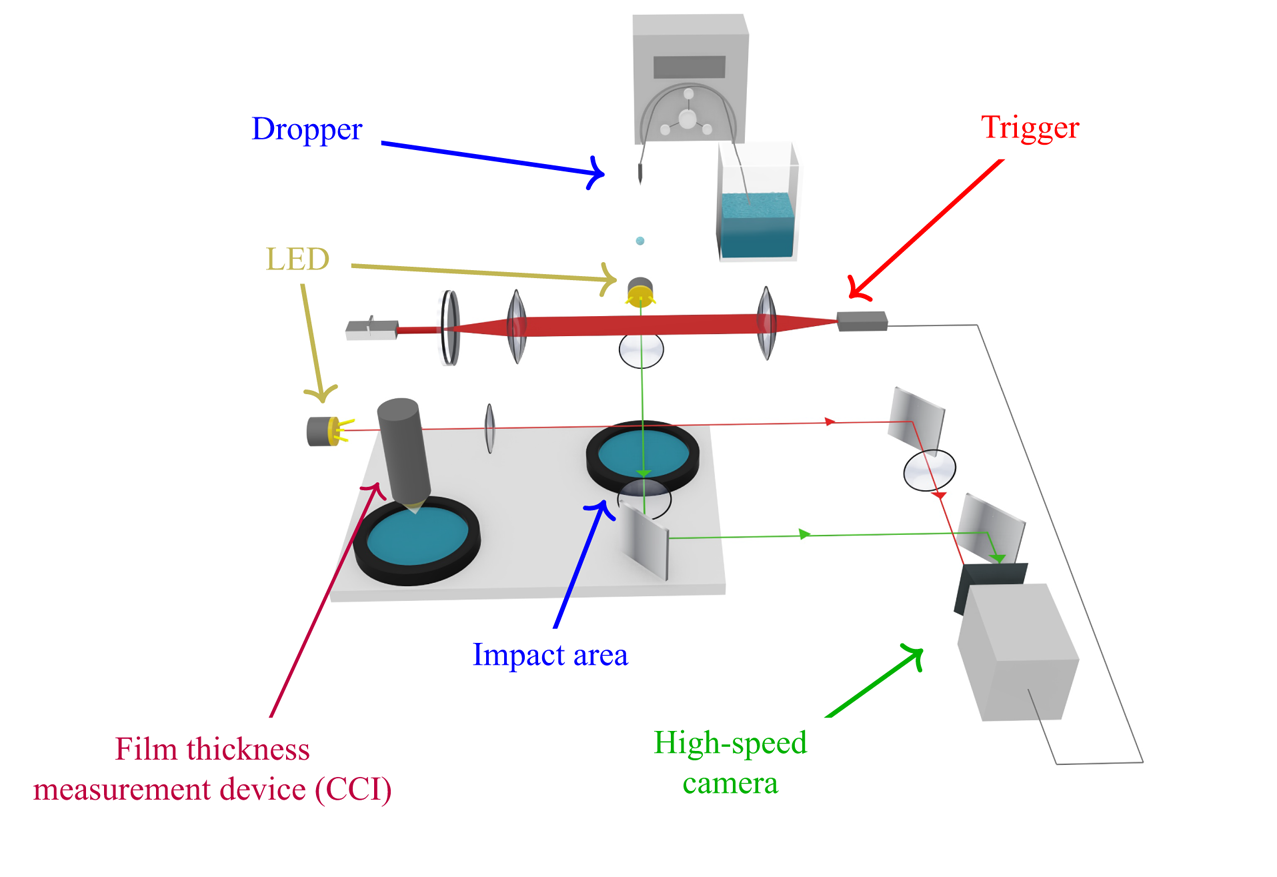
Figure 7. Schematic of the experimental set-up allowing a two-perspective high-speed shadowgraphy of the impact area by an arrangement of lenses and mirrors. Reprinted from Bernard et al. (Reference Bernard, Vaikuntanathan, Weigand and Lamanna2020) with permission from Elsevier Inc. (2020).
Finally, the images are binarized in order to detect the four edges of the crown like the four orange dots in figure 2. The distance between the detected crown edges enables the evaluation of the crown geometrical parameters: crown rim radius ![]() ${R_{R}}{}$ and crown base radius
${R_{R}}{}$ and crown base radius ![]() ${R_{B}}{}$ for the horizontal distances, and the crown rim height
${R_{B}}{}$ for the horizontal distances, and the crown rim height ![]() ${H_{R}}{}$ in the vertical. To detect these edges, the image is analysed pixel line by pixel line. At the bottom, a search for the maximum radius is carried out within the last five lines belonging to the crown. The detection of the crown rim is more difficult, especially when the rim has corrugations or fingers. For each pixel line at the crown top, the presence of fingers (alternation of black and white pixels) is checked for. The height of the crown
${H_{R}}{}$ in the vertical. To detect these edges, the image is analysed pixel line by pixel line. At the bottom, a search for the maximum radius is carried out within the last five lines belonging to the crown. The detection of the crown rim is more difficult, especially when the rim has corrugations or fingers. For each pixel line at the crown top, the presence of fingers (alternation of black and white pixels) is checked for. The height of the crown ![]() ${H_{R}}{}$ is set at the finger base, meaning that the corrugations due to the fingers are not taken into account.
${H_{R}}{}$ is set at the finger base, meaning that the corrugations due to the fingers are not taken into account.
Appendix B. Crown surface energies at  ${\delta {}}\approx 0.26$
${\delta {}}\approx 0.26$
The maximum crown surfaces ![]() $\varSigma _{c,max}{}$ and normalized crown surface energies
$\varSigma _{c,max}{}$ and normalized crown surface energies ![]() ${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ are given in figures 8(a) and 8(b), respectively, as a function of
${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ are given in figures 8(a) and 8(b), respectively, as a function of ![]() $\mathit {We}_{d}{}$ for the three different liquid pairs at
$\mathit {We}_{d}{}$ for the three different liquid pairs at ![]() ${\delta {}}\approx {} 0.26$. The trends observed are in general similar to those of
${\delta {}}\approx {} 0.26$. The trends observed are in general similar to those of ![]() ${\delta {}}\approx {} 0.12$: the points of the different liquid pairs come together if the interfacial energy between droplet and wall film is taken into account, the crown surface
${\delta {}}\approx {} 0.12$: the points of the different liquid pairs come together if the interfacial energy between droplet and wall film is taken into account, the crown surface ![]() $\varSigma _{c}{}$ tends to increase with growing
$\varSigma _{c}{}$ tends to increase with growing ![]() $\mathit {We}_{d}{}$ and
$\mathit {We}_{d}{}$ and ![]() ${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ tends to decrease with growing
${E_{\sigma ,c,max}}{}/{E_{k,d,0}}{}$ tends to decrease with growing ![]() $\mathit {We}_{d}{}$.
$\mathit {We}_{d}{}$.
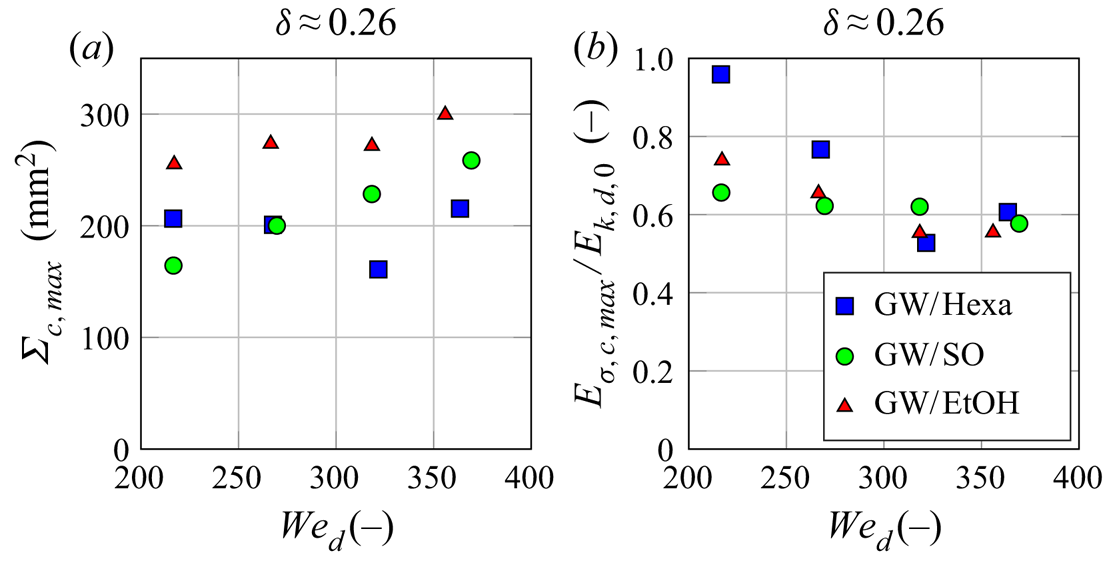
Figure 8. (a) Maximum crown surface ![]() $\varSigma _{c,max}{}$ at different Weber numbers
$\varSigma _{c,max}{}$ at different Weber numbers ![]() $\mathit {We}_{d}{}$. (b) Maximum crown surface energy
$\mathit {We}_{d}{}$. (b) Maximum crown surface energy ![]() ${E_{\sigma ,c,max}}{}$ normalized with the initial droplet kinetic energy
${E_{\sigma ,c,max}}{}$ normalized with the initial droplet kinetic energy ![]() ${E_{k,d,0}}{}$ at different Weber numbers
${E_{k,d,0}}{}$ at different Weber numbers ![]() $\mathit {We}_{d}{}$.
$\mathit {We}_{d}{}$.
Considering the crown surface energies (figure 8b), the values are higher than those of ![]() ${\delta {}}\approx {} 0.12$ as explained in § 4.1. However, some discrepancies are observed for small
${\delta {}}\approx {} 0.12$ as explained in § 4.1. However, some discrepancies are observed for small ![]() $\mathit {We}_{d}{}$, where the crown surfaces are much higher than expected. This is particularly pronounced for GW/Hexa, whose trend with decreasing
$\mathit {We}_{d}{}$, where the crown surfaces are much higher than expected. This is particularly pronounced for GW/Hexa, whose trend with decreasing ![]() $\mathit {We}_{d}{}$ is reversed, leading to crown surfaces even higher than those of GW/SO. Note that a similar trend is also observed for GW/Hexa at
$\mathit {We}_{d}{}$ is reversed, leading to crown surfaces even higher than those of GW/SO. Note that a similar trend is also observed for GW/Hexa at ![]() ${\delta {}}\approx {} 0.12$ for the lowest
${\delta {}}\approx {} 0.12$ for the lowest ![]() $\mathit {We}_{d}{}$, but in much smaller amplitude. This sudden increase is peculiar since it corresponds to higher values of normalized crown surface energies approaching 1, which would indicate extremely low losses. The possible reasons for these discrepancies are listed hereafter.
$\mathit {We}_{d}{}$, but in much smaller amplitude. This sudden increase is peculiar since it corresponds to higher values of normalized crown surface energies approaching 1, which would indicate extremely low losses. The possible reasons for these discrepancies are listed hereafter.
First, it is possible that these experimental conditions lead to a much better energy transfer from the incoming droplet kinetic energy to surface energy. Low Weber/Reynolds numbers and high wall-film thickness promote a smooth energy transfer, corresponding to a clear deposition case (or full deposition case), as is confirmed by the unperturbed rim of figure 9. Furthermore, no energy is lost to form the corrugations on the crown rim, and there is no mass loss. Since the interfacial tension of GW/Hexa is higher, this effect could happen at higher ![]() $\mathit {We}_{d}{}$ and stronger than for the other liquid pairs, as has been observed for the splashing limit and explained in § 3.1.
$\mathit {We}_{d}{}$ and stronger than for the other liquid pairs, as has been observed for the splashing limit and explained in § 3.1.
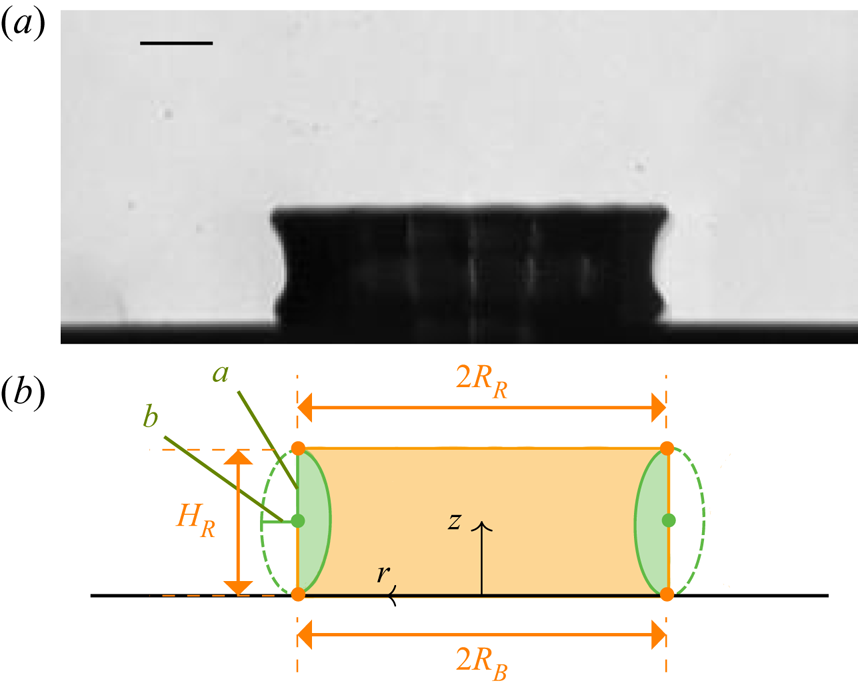
Figure 9. (a) Typical high-speed image (without background subtraction) of GW/Hexa at ![]() $\mathit {We}_{d}{}=320$ and
$\mathit {We}_{d}{}=320$ and ![]() $\delta {}\approx {}0.259$ (see full experimental condition in table 2). The scale bar measures 2.00 mm. (b) Schematic of a cylindrical crown with curved wall.
$\delta {}\approx {}0.259$ (see full experimental condition in table 2). The scale bar measures 2.00 mm. (b) Schematic of a cylindrical crown with curved wall.
Second, the particularly strong increase of GW/Hexa could be due to contamination that would decrease the value of the interfacial tension, and thus increase the crown extension. However, this effect alone is unlikely since it has been observed at several impact conditions, and also for all liquid pairs (GW/SO and GW/EtOH) although with smaller amplitude.
Last, part of this increasing trend could be due to measurement errors of the crown surface due to its concavity for these cases, especially for GW/Hexa as illustrated in figure 9. Similar crown contractions have already been observed in the literature for n-hexadecane droplet/wall-film experiments (Geppert et al. Reference Geppert, Terzis, Lamanna, Marengo and Weigand2017), but they were rather located at the top of the crown. In the present cases, this curvature of the crown wall could be due to the interfacial tension acting on it, since it is the most varying parameter between the three liquid pairs. It could also result from the gradient of the crown thickness and/or liquid properties inside the crown wall. To better understand these effects, the spatial distribution of the liquids need to be resolved, which goes beyond the scope of this study, but could be for example further investigated with direct numerical simulations.
Coming back to the evaluation of the crown surface, this crown wall bent inwards can lead to an overestimation of the real crown surface. Indeed, the crown surface is calculated by assuming a straight line between the rim and base radii (the crown wall being considered as a conical frustum, as in figure 2). In order to get a rough idea of this overestimation, one can compare the surface of a simplified cylindrical crown with the same crown where the sidewall is curved inward, as illustrated in figure 9(b). In this simplified case, the envelop of the crown wall is assumed to follow an ellipse centred at (![]() ${R_{R}}{},{H_{R}}{}/2$) and a vertical major axis
${R_{R}}{},{H_{R}}{}/2$) and a vertical major axis ![]() $a$ equal to
$a$ equal to ![]() ${{H_{R}}{}/2}$. The minor axis
${{H_{R}}{}/2}$. The minor axis ![]() $b$ can be varied to see the influence of the crown wall curvature. In this configuration, the crown radius
$b$ can be varied to see the influence of the crown wall curvature. In this configuration, the crown radius ![]() $r$ is dependent on the height
$r$ is dependent on the height ![]() $z$ as follows:
$z$ as follows:
 \begin{equation} r={{R_{R}}{}}-b\sqrt{1-\frac{\left({{H_{R}}{}}/2-z\right)^{2}}{a^{2}}}. \end{equation}
\begin{equation} r={{R_{R}}{}}-b\sqrt{1-\frac{\left({{H_{R}}{}}/2-z\right)^{2}}{a^{2}}}. \end{equation}The crown surface can be calculated as:
The solution of this integration for ![]() $a={H_{R}}{}/2$, normalized with the cylindrical surface of reference
$a={H_{R}}{}/2$, normalized with the cylindrical surface of reference ![]() $2{\rm \pi} {R_{R}}{}{H_{R}}{}$ is provided in function of the crown aspect ratio
$2{\rm \pi} {R_{R}}{}{H_{R}}{}$ is provided in function of the crown aspect ratio ![]() ${H_{R}}{}/{R_{R}}{}$ in figure 10 for different values of the minor axis
${H_{R}}{}/{R_{R}}{}$ in figure 10 for different values of the minor axis ![]() $b$.
$b$.

Figure 10. Normalized crown surface in the case where the crown wall is bent inwards as a function of the crown aspect ratio ![]() ${H_{R}}{}/{R_{R}}{}$, for different values of the minor axis
${H_{R}}{}/{R_{R}}{}$, for different values of the minor axis ![]() $b$ of the ellipse as shown in the schematic of figure 9(b). This quantifies the underestimation of the measured crown surface
$b$ of the ellipse as shown in the schematic of figure 9(b). This quantifies the underestimation of the measured crown surface ![]() $\varSigma _{c}{}$ when the crown wall is assumed to be a straight line between base and rim radii.
$\varSigma _{c}{}$ when the crown wall is assumed to be a straight line between base and rim radii.
For ![]() $b=0$, the coefficient is equal to one, the surfaces are equivalents. With increasing curvature, the ratio decreases, and it decreases also with increasing aspect ratio. The highest aspect ratio observed in the present database is
$b=0$, the coefficient is equal to one, the surfaces are equivalents. With increasing curvature, the ratio decreases, and it decreases also with increasing aspect ratio. The highest aspect ratio observed in the present database is ![]() ${H_{R}}{}/{R_{R}}{}=0.65$. The highest value of
${H_{R}}{}/{R_{R}}{}=0.65$. The highest value of ![]() $b$ can be estimated from the high-speed images. In figure 2, the value of
$b$ can be estimated from the high-speed images. In figure 2, the value of ![]() $b$ is approximately
$b$ is approximately ![]() $0.13{H_{R}}{}$, which is a particularly pronounced case. Hence, in the worst case scenario we consider the configuration of
$0.13{H_{R}}{}$, which is a particularly pronounced case. Hence, in the worst case scenario we consider the configuration of ![]() $b=0.15{H_{R}}{}$ with
$b=0.15{H_{R}}{}$ with ![]() ${H_{R}}{}/{R_{R}}{}=0.65$, which leads to an underestimation of almost 8 %.
${H_{R}}{}/{R_{R}}{}=0.65$, which leads to an underestimation of almost 8 %.









































































