Hostname: page-component-76c49bb84f-qtd2s Total loading time: 0 Render date: 2025-07-06T21:52:51.429Z Has data issue: false hasContentIssue false
  • English
  • Français

The minimum flow rate of electrosprays in the cone-jet mode

Published online by Cambridge University Press:  01 August 2019

Manuel Gamero-Castaño Open the ORCID record for Manuel Gamero-Castaño [Opens in a new window]  and
M. Magnani
Manuel Gamero-Castaño*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
M. Magnani
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
*
†Email address for correspondence: mgameroc@uci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Stable electrospraying in the cone-jet mode is restricted to flow rates above a minimum, and understanding the physics of this constraint is important to improve this atomization technique. We study this problem by measuring the minimum flow rate of electrosprays of tributyl phosphate and propylene carbonate at varying electrical conductivity 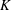$K$ (all other physical properties such as the density 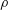$\unicode[STIX]{x1D70C}$, surface tension 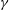$\unicode[STIX]{x1D6FE}$ and viscosity 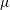$\unicode[STIX]{x1D707}$ are kept constant and equal to those of the pure liquids), and through the analysis of numerical solutions. The experiments show that the dimensionless minimum flow rate is a function of both the dielectric constant $\unicode[STIX]{x1D700}$ of the liquid and its Reynolds number, 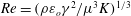$Re=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}_{o}\unicode[STIX]{x1D6FE}^{2}/\unicode[STIX]{x1D707}^{3}K)^{1/3}$. This result is unexpected in the light of existing theories which, for the conditions investigated, predict a minimum flow rate that depends only on $\unicode[STIX]{x1D700}$ and/or is marginally affected by 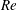$Re$. The experimental dependency on the Reynolds number requires the viscous stress to be a factor in the determination of the minimum flow rate. However, the numerical solutions suggest that a balance of opposing forces including the fixing viscous stress, which at decreasing flow rates may lower the acceleration of the flow to the point of making it unstable, is unlikely to be the cause. An alternative mechanism is the significant viscous dissipation taking place in the transition from cone to jet, and which at low flow rates cannot be supplied by the work done by the tangential electric stress in the same area. Instead, mechanical energy injected into the system farther downstream must be transferred upstream where dissipation predominantly takes place. This mechanism is supported by the balance between the energy dissipated and the work done by the electric stress in the transition from cone to jet, which yields a relationship between the minimum flow rate, the Reynolds number and the dielectric constant that compares well with experiments.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Electrohydrodynamic effects

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 553 - 572
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Chen, D. R., Pui, D. Y. H. & Kaufman, S. L. 1995 Electrospraying of conducting liquids for monodisperse aerosol generation in the 4 nm to 1. 8 μm diameter range. J. Aero. Sci. 26 (6), 963–977.Google Scholar
Cloupeau, M. & Prunet-Foch, B. 1989 Electrostatic spraying of liquids in cone-jet mode. J. Electrostat. 22 (2), 135–159.Google Scholar
Cloupeau, M. & Prunet-Foch, B. 1990 Electrostatic spraying of liquids. Main functioning modes. J. Electrostat. 25 (25), 165–184.Google Scholar
Fernández de la Mora, J. 2007 The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 39 (1), 217–243.Google Scholar
Fernández de la Mora, J. & Loscertales, I. G. 1994 The current emitted by highly conducting Taylor cones. J. Fluid Mech. 260, 155–184.Google Scholar
Gamero-Castaño, M. 2008 Characterization of the electrosprays of 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide in vacuum. Phys. Fluids 20 (3), 032103.Google Scholar
Gamero-Castaño, M. 2010 Energy dissipation in electrosprays and the geometric scaling of the transition region of cone-jets. J. Fluid Mech. 662, 493–513.Google Scholar
Gamero-Castaño, M. 2019 Dissipation in cone-jet electrosprays and departure from isothermal operation. Phys. Rev. E 99 (6), 061101(R).Google Scholar
Gamero-Castaño, M. & Hruby, V. 2001 Electrospray as a source of nanoparticles for efficient colloid thrusters. J. Propul. Power 17 (5), 977–987.Google Scholar
Gamero-Castaño, M. & Hruby, V. 2002 Electric measurements of charged sprays emitted by cone-jets. J. Fluid Mech. 459, 245–276.Google Scholar
Gamero-Castaño, M. & Magnani, M. 2019 Numerical simulation of electrospraying in the cone-jet mode. J. Fluid Mech. 859, 247–267.Google Scholar
Gañán-Calvo, A. M. 1997 Cone-jet analytical extension of Taylor’s electrostatic solution and the asymptotic universal scaling laws in electrospraying. Phys. Rev. Lett. 79 (2), 217–220.Google Scholar
Gañán-Calvo, A. M. 1999 The surface charge in electrospraying: its nature and its universal scaling laws. J. Aero. Sci. 30 (7), 863–872.Google Scholar
Gañán-Calvo, A. M. 2004 On the general scaling theory for electrospraying. J. Fluid Mech. 507, 203–212.Google Scholar
Gañán-Calvo, A. M., Dávila, J. & Barrero, A. 1997 Current and droplet size in the electrospraying of liquids. Scaling laws. J. Aero. Sci. 28 (2), 249–275.Google Scholar
Gañán-Calvo, A. M., López-Herrera, J. M., Herrada, M. A., Ramos, A. & Montanero, J. M. 2018 Review on the physics of electrospray: from electrokinetics to the operating conditions of single and coaxial Taylor cone-jets, and AC electrospray. J. Aero. Sci. 125, 32–56.Google Scholar
Gañán-Calvo, A. M., Rebollo-Muñóz, N. & Montanero, J. M. 2013 The minimum or natural rate of flow and droplet size ejected by Taylor conejets: physical symmetries and scaling laws. New J. Phys. 79 (15), 033035.Google Scholar
Grustan-Gutierrez, E. & Gamero-Castaño, M. 2017 Microfabricated electrospray thruster array with high hydraulic resistance channels. J. Propul. Power 33 (4), 984–991.Google Scholar
Higuera, F. J. 2003 Flow rate and electric current emitted by a Taylor cone. J. Fluid Mech. 484, 303–327.Google Scholar
Higuera, F. J. 2017 Qualitative analysis of the minimum flow rate of a cone-jet of a very polar liquid. J. Fluid Mech. 816, 428–441.Google Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111–146.Google Scholar
Ponce-Torres, A., Rebollo-Muñóz, N., Herrada, M. A., Gañán-Calvo, A. M. & Montanero, J. M. 2018 The steady cone-jet mode of electrospraying close to the minimum volume stability limit. J. Fluid Mech. 857, 142–172.Google Scholar
Riddick, J. A., Bunger, W. B. & Sakano, T. K. 1986 Organic Solvents: Physical Properties and Methods of Purification, 4th edn. Techniques of Chemistry, vol. II. Wiley.Google Scholar
Rosell-Llompart, J. & Fernández de la Mora, J. 1994 Generation of monodisperse droplets 0.3 to 4 μm in diameter from electrified cone-jets of highly conducting and viscous-liquids. J. Aero. Sci. 25 (6), 1093–1119.Google Scholar
Rosell-Llompart, J., Grifoll, J. & Loscertales, I. G. 2018 Electrosprays in the cone-jet mode: from Taylor cone formation to spray development. J. Aero. Sci. 125, 2–31.Google Scholar
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29 (1), 27–64.Google Scholar
Scheideler, W. J. & Chen, C. H. 2014 The minimum flow rate scaling of Taylor cone-jets issued from a nozzle. Appl. Phys. Lett. 104 (2), 024103.Google Scholar
Taylor, G. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A 280 (1382), 383–397.Google Scholar
Zeleny, J. 1914 The electrical discharge from liquid points, and a hydrostatic method of measuring the electric intensity at their surfaces. Phys. Rev. 3 (2), 69–91.Google Scholar