Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Limare, A.
Fourel, L.
Surducan, E.
Neamtu, C.
Surducan, V.
Vilella, K.
Farnetani, C. G.
Kaminski, E.
and
Jaupart, C.
2015.
Microwave-based, internally-heated convection: New perspectives for the heterogeneous case.
Vol. 1700,
Issue. ,
p.
040001.
Boutelier, D.
Cruden, A.
and
Saumur, B.
2016.
Density and visco-elasticity of Natrosol 250 HH solutions: Determining their suitability for experimental tectonics.
Journal of Structural Geology,
Vol. 86,
Issue. ,
p.
153.
Vilella, Kenny
and
Deschamps, Frédéric
2017.
Thermal convection as a possible mechanism for the origin of polygonal structures on Pluto's surface.
Journal of Geophysical Research: Planets,
Vol. 122,
Issue. 5,
p.
1056.
Fourel, Loïc
Limare, Angela
Jaupart, Claude
Surducan, Emanoil
Farnetani, Cinzia G.
Kaminski, Edouard C.
Neamtu, Camelia
and
Surducan, Vasile
2017.
The Earth’s mantle in a microwave oven: thermal convection driven by a heterogeneous distribution of heat sources.
Experiments in Fluids,
Vol. 58,
Issue. 8,
Smrekar, Suzanne E.
Davaille, Anne
and
Sotin, Christophe
2018.
Venus Interior Structure and Dynamics.
Space Science Reviews,
Vol. 214,
Issue. 5,
Armitage, John J.
and
Collier, Jenny S.
2018.
The thermal structure of volcanic passive margins.
Petroleum Geoscience,
Vol. 24,
Issue. 4,
p.
393.
Di Giuseppe, Erika
2018.
Reference Module in Earth Systems and Environmental Sciences.
Lepot, Simon
Aumaître, Sébastien
and
Gallet, Basile
2018.
Radiative heating achieves the ultimate regime of thermal convection.
Proceedings of the National Academy of Sciences,
Vol. 115,
Issue. 36,
p.
8937.
Bouillaut, Vincent
Lepot, Simon
Aumaître, Sébastien
and
Gallet, Basile
2019.
Transition to the ultimate regime in a radiatively driven convection experiment.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
Steinke, T.
Hu, H.
Höning, D.
van der Wal, W.
and
Vermeersen, B.
2020.
Tidally induced lateral variations of Io's interior.
Icarus,
Vol. 335,
Issue. ,
p.
113299.
Kaminski, Edouard
Limare, Angela
Kenda, Balthasar
and
Chaussidon, Marc
2020.
Early accretion of planetesimals unraveled by the thermal evolution of the parent bodies of magmatic iron meteorites.
Earth and Planetary Science Letters,
Vol. 548,
Issue. ,
p.
116469.
Zaussinger, Florian
Haun, Peter
Szabo, Peter S. B.
Travnikov, Vadim
Al Kawwas, Mustafa
and
Egbers, Christoph
2020.
Rotating spherical gap convection in the GeoFlow International Space Station (ISS) experiment.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Limare, Angela
Kenda, Balthasar
Kaminski, Edouard
Surducan, Emanoil
Surducan, Vasile
and
Neamtu, Camelia
2021.
Transient convection experiments in internally-heated systems.
MethodsX,
Vol. 8,
Issue. ,
p.
101224.
Sturtz, Cyril
Kaminski, Édouard
Limare, Angela
and
Tait, Stephen
2021.
The fate of particles in a volumetrically heated convective fluid at high Prandtl number.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Lenardic, A.
Seales, J.
Moore, W.
and
Weller, M.
2021.
Convective and Tectonic Plate Velocities in a Mixed Heating Mantle.
Geochemistry, Geophysics, Geosystems,
Vol. 22,
Issue. 2,
Agasthya, Lokahith
Bartel, Andreas
Biferale, Luca
Ehrhardt, Matthias
and
Toschi, Federico
2022.
Large-scale convective flow sustained by thermally active Lagrangian tracers.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Kazemi, Sina
Ostilla-Mónico, Rodolfo
and
Goluskin, David
2022.
Transition between Boundary-Limited Scaling and Mixing-Length Scaling of Turbulent Transport in Internally Heated Convection.
Physical Review Letters,
Vol. 129,
Issue. 2,
Sturtz, Cyril
Limare, Angela
Tait, Stephen
and
Kaminski, Édouard
2022.
Birth and Decline of Magma Oceans in Planetesimals: 1. Experimental Study of Erosion and Deposition of Particles in an Internally Heated Convecting Fluid.
Journal of Geophysical Research: Planets,
Vol. 127,
Issue. 12,
CHOBLET, Gaël
2025.
Structure and Dynamics of the Earth's Interior 1.
p.
1.
FARNETANI, Cinzia G.
2025.
Structure and Dynamics of the Earth's Interior 1.
p.
115.
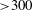 ${>}300$ ) and high Rayleigh–Roberts number (ranging from
${>}300$ ) and high Rayleigh–Roberts number (ranging from 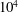 $10^{4}$ to
$10^{4}$ to 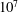 $10^{7}$ ), appropriate for planetary mantle convection. Non-invasive techniques are employed to determine both temperature and velocity fields. We successfully validate the experimental results by conducting numerical simulations in three-dimensional Cartesian geometry that reproduce the experimental conditions. Scaling laws relating key characteristics of the thermal boundary layer, namely its thickness and temperature drop, to the Rayleigh–Roberts number have been established for both rigid and free-slip boundary conditions. A robust conclusion is that for rigid boundary conditions the internal temperature is significantly higher than for free-slip boundary conditions. Our scaling laws, coupled with plausible physical parameters entering the Rayleigh–Roberts number, enable us to calculate the mantle potential temperature for the Earth and Venus, two telluric planets with different mechanical boundary conditions at their surface.
$10^{7}$ ), appropriate for planetary mantle convection. Non-invasive techniques are employed to determine both temperature and velocity fields. We successfully validate the experimental results by conducting numerical simulations in three-dimensional Cartesian geometry that reproduce the experimental conditions. Scaling laws relating key characteristics of the thermal boundary layer, namely its thickness and temperature drop, to the Rayleigh–Roberts number have been established for both rigid and free-slip boundary conditions. A robust conclusion is that for rigid boundary conditions the internal temperature is significantly higher than for free-slip boundary conditions. Our scaling laws, coupled with plausible physical parameters entering the Rayleigh–Roberts number, enable us to calculate the mantle potential temperature for the Earth and Venus, two telluric planets with different mechanical boundary conditions at their surface.

