Article contents
Material stability and instability in non-local continuum models for dense granular materials
Published online by Cambridge University Press: 28 May 2019
Abstract
A class of common and successful continuum models for steady, dense granular flows is based on the 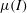 $\unicode[STIX]{x1D707}(I)$ model for viscoplastic grain-inertial rheology. Recent work has shown that under certain conditions,
$\unicode[STIX]{x1D707}(I)$ model for viscoplastic grain-inertial rheology. Recent work has shown that under certain conditions, 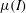 $\unicode[STIX]{x1D707}(I)$-based models display a linear instability in which short-wavelength perturbations grow at an unbounded rate – i.e. a Hadamard instability. This observation indicates that
$\unicode[STIX]{x1D707}(I)$-based models display a linear instability in which short-wavelength perturbations grow at an unbounded rate – i.e. a Hadamard instability. This observation indicates that 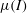 $\unicode[STIX]{x1D707}(I)$ models will predict strain localization arising due to material instability in dense granular materials; however, it also raises concerns regarding the robustness of numerical solutions obtained using these models. Several approaches to regularizing this instability have been suggested in the literature. Among these, it has been shown that the inclusion of higher-order velocity gradients into the constitutive equations can suppress the Hadamard instability, while not precluding the modelling of strain localization into diffuse shear bands. In our recent work (Henann & Kamrin, Proc. Natl Acad. Sci. USA, vol. 110, 2013, pp. 6730–6735), we have proposed a non-local model – called the non-local granular fluidity (NGF) model – which also involves higher-order flow gradients and has been shown to quantitatively describe a wide variety of steady, dense flows. In this work, we show that the NGF model also successfully regularizes the Hadamard instability of the
$\unicode[STIX]{x1D707}(I)$ models will predict strain localization arising due to material instability in dense granular materials; however, it also raises concerns regarding the robustness of numerical solutions obtained using these models. Several approaches to regularizing this instability have been suggested in the literature. Among these, it has been shown that the inclusion of higher-order velocity gradients into the constitutive equations can suppress the Hadamard instability, while not precluding the modelling of strain localization into diffuse shear bands. In our recent work (Henann & Kamrin, Proc. Natl Acad. Sci. USA, vol. 110, 2013, pp. 6730–6735), we have proposed a non-local model – called the non-local granular fluidity (NGF) model – which also involves higher-order flow gradients and has been shown to quantitatively describe a wide variety of steady, dense flows. In this work, we show that the NGF model also successfully regularizes the Hadamard instability of the 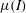 $\unicode[STIX]{x1D707}(I)$ model. We further apply the NGF model to the problem of strain localization in quasi-static plane-strain compression using nonlinear finite-element simulations in order to demonstrate that the model is capable of describing diffuse strain localization in a mesh-independent manner. Finally, we consider the linear stability of an alternative gradient–viscoplastic model (Bouzid et al., Phys. Rev. Lett., vol. 111, 2013, 238301) and show that the inclusion of higher-order gradients does not guarantee the suppression of the Hadamard instability.
$\unicode[STIX]{x1D707}(I)$ model. We further apply the NGF model to the problem of strain localization in quasi-static plane-strain compression using nonlinear finite-element simulations in order to demonstrate that the model is capable of describing diffuse strain localization in a mesh-independent manner. Finally, we consider the linear stability of an alternative gradient–viscoplastic model (Bouzid et al., Phys. Rev. Lett., vol. 111, 2013, 238301) and show that the inclusion of higher-order gradients does not guarantee the suppression of the Hadamard instability.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by

