Article contents
Localised continental shelf waves: geometric effects and resonant forcing
Published online by Cambridge University Press: 11 November 2015
Abstract
Alongshore variations in coastline curvature or offshore depth profile can create localised regions of shelf-wave propagation with modes decaying outside these regions. These modes, termed localised continental shelf waves ( 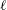 $\ell$ CSWs) here, exist only at certain discrete frequencies lying below the local maximum frequency, and above the far-field maximum frequency, for propagating shelf waves. The purpose of this paper is to obtain these frequencies and construct, both analytically and numerically, and discuss
$\ell$ CSWs) here, exist only at certain discrete frequencies lying below the local maximum frequency, and above the far-field maximum frequency, for propagating shelf waves. The purpose of this paper is to obtain these frequencies and construct, both analytically and numerically, and discuss 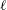 $\ell$ CSWs for shelves with arbitrary alongshore variations in offshore depth profile and coastline curvature. If the shelf curvature changes by a small fraction of its value over the shelf section of interest or an alongshore perturbation in offshore depth profile varies slowly over the same length scale then
$\ell$ CSWs for shelves with arbitrary alongshore variations in offshore depth profile and coastline curvature. If the shelf curvature changes by a small fraction of its value over the shelf section of interest or an alongshore perturbation in offshore depth profile varies slowly over the same length scale then 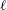 $\ell$ CSWs can be constructed using WKBJ theory. Two subcases are described: (i) if the propagating region is sufficiently long that the offshore structure of the
$\ell$ CSWs can be constructed using WKBJ theory. Two subcases are described: (i) if the propagating region is sufficiently long that the offshore structure of the 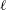 $\ell$ CSW varies appreciably alongshore then the frequency and alongshore structure are found from a sequence of local problems; (ii) if the propagating region is sufficiently short that the alongshore change in offshore structure of the
$\ell$ CSW varies appreciably alongshore then the frequency and alongshore structure are found from a sequence of local problems; (ii) if the propagating region is sufficiently short that the alongshore change in offshore structure of the 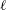 $\ell$ CSW is small then the alongshore modal structure is given in an explicit, uniformly valid form. A separate asymptotic theory is required for curvature perturbations to shelves that are otherwise straight rather than curved. Comparison with highly accurately numerically determined
$\ell$ CSW is small then the alongshore modal structure is given in an explicit, uniformly valid form. A separate asymptotic theory is required for curvature perturbations to shelves that are otherwise straight rather than curved. Comparison with highly accurately numerically determined 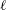 $\ell$ CSWs shows that both theories are extremely accurate, with the WKBJ theory having a significantly wider range of applicability. An idealised model for the generation of
$\ell$ CSWs shows that both theories are extremely accurate, with the WKBJ theory having a significantly wider range of applicability. An idealised model for the generation of 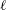 $\ell$ CSWs is also suggested. A localised time-periodic wind stress generates an evanescent continental shelf wave in the far field of a localised mode where the coast is almost straight and the response on the shelf is obtained numerically. If the forcing frequency is close to that of an
$\ell$ CSWs is also suggested. A localised time-periodic wind stress generates an evanescent continental shelf wave in the far field of a localised mode where the coast is almost straight and the response on the shelf is obtained numerically. If the forcing frequency is close to that of an 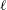 $\ell$ CSW then the wind stress excites energetic motions in the region of maximum curvature, creating a significant localised response possibly far from the forcing region.
$\ell$ CSW then the wind stress excites energetic motions in the region of maximum curvature, creating a significant localised response possibly far from the forcing region.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 4
- Cited by


