Hostname: page-component-76c49bb84f-c7tcl Total loading time: 0 Render date: 2025-07-03T03:46:54.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of magnetohydrodynamic flow in a square duct with thin conducting walls

Published online by Cambridge University Press:  22 December 2015

Jānis Priede ,
Thomas Arlt  and
Leo Bühler
Jānis Priede*
Affiliation:
Applied Mathematics Research Centre, Coventry University, Coventry CV1 5FB, UK
Thomas Arlt
Affiliation:
Institut für Kern- und Energietechnik, Karlsruhe Institute of Technology, von-Helmholtz-Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany
Leo Bühler
Affiliation:
Institut für Kern- und Energietechnik, Karlsruhe Institute of Technology, von-Helmholtz-Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany
*
†Email address for correspondence: J.Priede@coventry.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This study is concerned with the numerical linear stability analysis of liquid-metal flow in a square duct with thin electrically conducting walls subject to a uniform transverse magnetic field. We derive an asymptotic solution for the base flow that is valid for not only high but also moderate magnetic fields. This solution shows that, for low wall conductance ratios 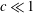$c\ll 1$, an extremely strong magnetic field with Hartmann number 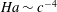$\mathit{Ha}\sim c^{-4}$ is required to attain the asymptotic flow regime considered in previous studies. We use a vector streamfunction–vorticity formulation and a Chebyshev collocation method to solve the eigenvalue problem for three-dimensional small-amplitude perturbations in ducts with realistic wall conductance ratios 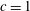$c=1$, 0.1 and 0.01 and Hartmann numbers up to 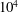$10^{4}$. As for similar flows, instability in a sufficiently strong magnetic field is found to occur in the sidewall jets with characteristic thickness 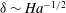${\it\delta}\sim \mathit{Ha}^{-1/2}$. This results in the critical Reynolds number and wavenumber increasing asymptotically with the magnetic field as 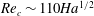$\mathit{Re}_{c}\sim 110\mathit{Ha}^{1/2}$ and 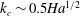$k_{c}\sim 0.5\mathit{Ha}^{1/2}$. The respective critical Reynolds number based on the total volume flux in a square duct with 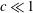$c\ll 1$ is 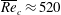$\overline{\mathit{Re}}_{c}\approx 520$. Although this value is somewhat larger than 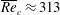$\overline{\mathit{Re}}_{c}\approx 313$ found by Ting et al. (Intl J. Engng Sci., vol. 29 (8), 1991, pp. 939–948) for the asymptotic sidewall jet profile, it still appears significantly lower than the Reynolds numbers at which turbulence is observed in experiments as well as in direct numerical simulations of this type of flow.

JFM classification

MHD and Electrohydrodynamics: High-Hartmann-number flows Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 129 - 146
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
Bühler, L. 2007 Liquid metal magnetohydrodynamics for fusion blankets. In Magnetohydrodynamics: Historical Evolution and Trends, vol. 80, pp. 171–194. Springer.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2007 Spectral Methods: Fundamentals in Single Domains. Springer.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chang, C. C. & Lundgren, Th. S. 1961 Duct flow in magnetohydrodynamics. Z. Angew. Math. Phys. 12 (2), 100–114.Google Scholar
Hagan, J. & Priede, J. 2014 Two-dimensional nonlinear travelling waves in magnetohydrodynamic channel flow. J. Fluid Mech. 760, 387–406.Google Scholar
Hartmann, J. 1937 Hg-dynamics I: theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (6), 1–28.Google Scholar
Hartmann, J. & Lazarus, F. 1937 Hg-dynamics II: experimental investigations on the flow of mercury in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 15 (7), 1–45.Google Scholar
Hollerbach, R. & Rüdiger, G. 2005 New type of magnetorotational instability in cylindrical Taylor–Couette flow. Phys. Rev. Lett. 95 (12), 124501.Google Scholar
Hunt, J. C. R. 1965 Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 21 (4), 577–590.CrossRefGoogle Scholar
Jackson, J. D. 1998 Classical Electrodynamics. Wiley.Google Scholar
Kinet, M., Knaepen, B. & Molokov, S. 2009 Instabilities and transition in magnetohydrodynamic flows in ducts with electrically conducting walls. Phys. Rev. Lett. 103 (15), 154501.Google Scholar
Krasnov, D., Thess, A., Boeck, Th., Zhao, Y. & Zikanov, O. 2013 patterned turbulence in liquid metal flow: computational reconstruction of the Hartmann experiment. Phys. Rev. Lett. 110 (8), 084501.Google Scholar
Pothérat, A. 2007 Quasi-two-dimensional perturbations in duct flows under transverse magnetic field. Phys. Fluids 19 (7), 074104.Google Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2010 Linear stability of Hunt’s flow. J. Fluid Mech. 649, 115–134.Google Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2012 Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct. J. Fluid Mech. 708, 111–127.Google Scholar
Priede, J., Grants, I. & Gerbeth, G. 2007 Inductionless magnetorotational instability in a Taylor–Couette flow with a helical magnetic field. Phys. Rev. E 75 (4), 47303.Google Scholar
Roberts, P. H. 1967 An Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Shatrov, V. & Gerbeth, G. 2010 Marginal turbulent magnetohydrodynamic flow in a square duct. Phys. Fluids 22 (8), 084101.Google Scholar
Shercliff, J. A. 1953 Steady motion of conducting fluids in pipes under transverse magnetic fields. Proc. Camb. Phil. Soc. 49 (1), 136–144.Google Scholar
Tatsumi, T. & Yoshimura, T. 1990 Stability of the laminar flow in a rectangular duct. J. Fluid Mech. 212, 437–449.CrossRefGoogle Scholar
Ting, A. L., Walker, J. S., Moon, T. J., Reed, C. B. & Picologlou, B. F. 1991 Linear stability analysis for high-velocity boundary layers in liquid-metal magnetohydrodynamic flows. Intl J. Engng Sci. 29 (8), 939–948.CrossRefGoogle Scholar
Uflyand, Ya. S. 1961 Flow stability of a conducting fluid in a rectangular channel in a transverse magnetic field. Sov. Phys. Tech. Phys. 5 (10), 1191–1193.Google Scholar
Uhlmann, M. & Nagata, M. 2006 Linear stability of flow in an internally heated rectangular duct. J. Fluid Mech. 551, 387–404.Google Scholar
Walker, J. S. 1981 Magneto-hydrodynamic flows in rectangular ducts with thin conducting walls. J. Méc. 20 (1), 79–112.Google Scholar
Zikanov, O., Krasnov, D., Boeck, T., Thess, A. & Rossi, M. 2014 Laminar–turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 66 (3), 030802.Google Scholar