Article contents
The linear instability of the stratified plane Couette flow
Published online by Cambridge University Press: 23 August 2018
Abstract
We present the stability analysis of a plane Couette flow which is stably stratified in the vertical direction orthogonal to the horizontal shear. Interest in such a flow comes from geophysical and astrophysical applications where background shear and vertical stable stratification commonly coexist. We perform the linear stability analysis of the flow in a domain which is periodic in the streamwise and vertical directions and confined in the cross-stream direction. The stability diagram is constructed as a function of the Reynolds number 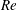 $Re$ and the Froude number
$Re$ and the Froude number 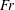 $Fr$, which compares the importance of shear and stratification. We find that the flow becomes unstable when shear and stratification are of the same order (i.e.
$Fr$, which compares the importance of shear and stratification. We find that the flow becomes unstable when shear and stratification are of the same order (i.e. 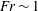 $Fr\sim 1$) and above a moderate value of the Reynolds number
$Fr\sim 1$) and above a moderate value of the Reynolds number 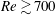 $Re\gtrsim 700$. The instability results from a wave resonance mechanism already known in the context of channel flows – for instance, unstratified plane Couette flow in the shallow-water approximation. The result is confirmed by fully nonlinear direct numerical simulations and, to the best of our knowledge, constitutes the first evidence of linear instability in a vertically stratified plane Couette flow. We also report the study of a laboratory flow generated by a transparent belt entrained by two vertical cylinders and immersed in a tank filled with salty water, linearly stratified in density. We observe the emergence of a robust spatio-temporal pattern close to the threshold values of
$Re\gtrsim 700$. The instability results from a wave resonance mechanism already known in the context of channel flows – for instance, unstratified plane Couette flow in the shallow-water approximation. The result is confirmed by fully nonlinear direct numerical simulations and, to the best of our knowledge, constitutes the first evidence of linear instability in a vertically stratified plane Couette flow. We also report the study of a laboratory flow generated by a transparent belt entrained by two vertical cylinders and immersed in a tank filled with salty water, linearly stratified in density. We observe the emergence of a robust spatio-temporal pattern close to the threshold values of 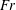 $Fr$ and
$Fr$ and 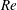 $Re$ indicated by linear analysis, and explore the accessible part of the stability diagram. With the support of numerical simulations we conclude that the observed pattern is a signature of the same instability predicted by the linear theory, although slightly modified due to streamwise confinement.
$Re$ indicated by linear analysis, and explore the accessible part of the stability diagram. With the support of numerical simulations we conclude that the observed pattern is a signature of the same instability predicted by the linear theory, although slightly modified due to streamwise confinement.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 23
- Cited by

