Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T16:21:04.909Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear biglobal analysis of Rayleigh–Bénard instabilities in binary fluids with and without throughflow

Published online by Cambridge University Press:  19 October 2012

Jun Hu ,
Daniel Henry ,
Xie-Yuan Yin  and
Hamda BenHadid
Jun Hu*
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
Daniel Henry
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, Ecole Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
Xie-Yuan Yin
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
Hamda BenHadid
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS/Université de Lyon, Ecole Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully CEDEX, France
*
†Email address for correspondence: hu_jun@iapcm.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Three-dimensional Rayleigh–Bénard instabilities in binary fluids with Soret effect are studied by linear biglobal stability analysis. The fluid is confined transversally in a duct and a longitudinal throughflow may exist or not. A negative separation factor 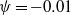$\psi = \ensuremath{-} 0. 01$ , giving rise to oscillatory transitions, has been considered. The numerical dispersion relation associated with this stability problem is obtained with a two-dimensional Chebyshev collocation method. Symmetry considerations are used in the analysis of the results, which allow the classification of the perturbation modes as 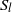${S}_{l} $ modes (those which keep the left–right symmetry) or 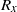${R}_{x} $ modes (those which keep the symmetry of rotation of 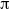$\lrm{\pi} $ about the longitudinal mid-axis). Without throughflow, four dominant pairs of travelling transverse modes with finite wavenumbers 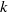$k$ have been found. Each pair corresponds to two symmetry degenerate left and right travelling modes which have the same critical Rayleigh number 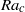${\mathit{Ra}}_{c} $ . With the increase of the duct aspect ratio 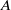$A$ , the critical Rayleigh numbers for these four pairs of modes decrease and closely approach the critical value 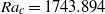${\mathit{Ra}}_{c} = 1743. 894$ obtained in a two-dimensional situation, one of the mode (a 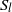${S}_{l} $ mode called mode A) always remaining the dominant mode. Oscillatory longitudinal instabilities ( 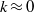$k\approx 0$ ) corresponding to either 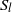${S}_{l} $ or 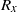${R}_{x} $ modes have also been found. Their critical curves, globally decreasing, present oscillatory variations when the duct aspect ratio 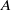$A$ is increased, associated with an increasing number of longitudinal rolls. When a throughflow is applied, the symmetry degeneracy of the pairs of travelling transverse modes is broken, giving distinct upstream and downstream modes. For small and moderate aspect ratios 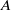$A$ , the overall critical Rayleigh number in the small Reynolds number range studied is only determined by the upstream transverse mode A. In contrast, for larger aspect ratios as 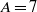$A= 7$ , different modes are successively dominant as the Reynolds number is increased, involving both upstream and downstream transverse modes A and even the longitudinal mode.

JFM classification

Convection: Buoyancy-driven instability Convection: Double diffusive convection

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 216 - 242
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Büchel, P. & Lücke, M. 2000a Influence of through flow on binary fluid convection. Phys. Rev. E 61, 3793–3810.Google Scholar
Büchel, P. & Lücke, M. 2000b Localized perturbations in binary fluid convection with and without throughflow. Phys. Rev. E 63, 016307.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2006 Spectral Methods: Fundamentals in Single Domains. Springer.Google Scholar
Carrière, Ph. & Monkewitz, P. A. 1999 Convective versus absolute instability in mixed Rayleigh–Bénard–Poiseuille convection. J. Fluid Mech. 384, 243–262.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112.CrossRefGoogle Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33, 21–32.Google Scholar
Hu, J., Ben Hadid, H. & Henry, D. 2007 Linear stability analysis of Poiseuille–Rayleigh–Bénard flows in binary fluids with Soret effect. Phys. Fluids 19, 034101.Google Scholar
Hu, J., Yin, X. Y., Ben Hadid, H. & Henry, D. 2009 Spatiotemporal evolution of Poiseuille–Rayleigh–Bénard flows in binary fluids with Soret effect under initial pulselike disturbances. Phys. Rev. E 80, 026312.Google Scholar
Jung, Ch., Lücke, M. & Büchel, P. 1996 Influence of through-flow on linear pattern formation properties in binary mixture convection. Phys. Rev. E 54, 1510–1529.CrossRefGoogle ScholarPubMed
Jung, D. & Lücke, M. 2005 Traveling wave fronts and localized traveling wave convection in binary fluid mixtures. Phys. Rev. E 72, 026307.Google Scholar
Kato, Y. & Fujimura, K. 2000 Prediction of pattern selection due to an interaction between longitudinal rolls and transverse modes in a flow through a rectangular channel heated from below. Phys. Rev. E 62, 601–611.CrossRefGoogle Scholar
Lehoucq, R. B. & Sorensen, D. C. 1996 Deflation techniques for an implicitly re-started Arnoldi iteration. SIAM J. Matrix Anal. Appl. 17, 789–821.Google Scholar
Luijkx, J. M. & Platten, J. K. 1981 On the onset of free convection in a rectangular channel. J. Non-Equilib. Thermodyn. 6, 141–158.Google Scholar
Luijkx, J. M., Platten, J. K. & Legros, J. C. 1981 On the existence of thermoconvective rolls, transverse to a superimposed mean Poiseuille flow. Intl J. Heat Mass Transfer 24, 1287–1291.Google Scholar
Müller, H. W., Lücke, M. & Kamps, M. 1992 Transversal convection patterns in horizontal shear flow. Phys. Rev. A 45, 3714–3726.Google Scholar
Müller, H. W., Tveitereid, M. & Trainoff, S. 1993 Rayleigh–Bénard problem with imposed weak through-flow: two coupled Ginzburg–Landau equations. Phys. Rev. E 48, 263–272.Google Scholar
Nicolas, X., Luijkx, J. M. & Platten, J. K. 2000 Linear stability of mixed convection flows in horizontal rectangular channels of finite transversal extension heated from below. Intl J. Heat Mass Transfer 43, 589–610.Google Scholar
Nicolas, X., Mojtabi, A. & Platten, J. K. 1997 Two-dimensional numerical analysis of the Poiseuille–Bénard flow in a rectangular channel heated from below. Phys. Fluids 9, 337–348.Google Scholar
Ouazzani, M. T., Platten, J. K. & Mojtabi, A. 1990 Etude expérimentale de la convection mixte entre deux plans horizontaux à températures différentes – II. Intl J. Heat Mass Transfer 33, 1417–1427.CrossRefGoogle Scholar
Ouazzani, M. T., Platten, J. K., Müller, H. W. & Lücke, M. 1995 Etude de la convection mixte entre deux plans horizontaux à températures différentes – III. Intl J. Heat Mass Transfer 38, 875–886.Google Scholar
Platten, J. K. & Legros, J. C. 1984 Convection in Liquids. Springer.Google Scholar
Rosenhead, L. 1963 Laminar Boundary Layers. Oxford University Press.Google Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39, 249–315.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar