Article contents
Large-eddy simulation of temporally developing double helical vortices
Published online by Cambridge University Press: 23 January 2019
Abstract
This paper investigates the transient regime and turbulent wake characteristics of temporally developing double helical vortices via high-fidelity large-eddy simulation (LES) for circulation Reynolds numbers in the range 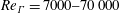 $Re_{\unicode[STIX]{x1D6E4}}=7000{-}70\,000$, vortex-core radii between
$Re_{\unicode[STIX]{x1D6E4}}=7000{-}70\,000$, vortex-core radii between 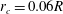 $r_{c}=0.06R$ and
$r_{c}=0.06R$ and 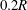 $0.2R$ and helical pitches in the range
$0.2R$ and helical pitches in the range 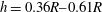 $h=0.36R{-}0.61R$, where
$h=0.36R{-}0.61R$, where 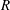 $R$ is the initial helix radius. The present study achieves three objectives: (i) assess the influence of
$R$ is the initial helix radius. The present study achieves three objectives: (i) assess the influence of 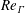 $Re_{\unicode[STIX]{x1D6E4}}$,
$Re_{\unicode[STIX]{x1D6E4}}$, 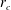 $r_{c}$ and
$r_{c}$ and 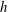 $h$ on the growth rates of the helical vortex instability driven by mutual inductance; (ii) characterize the type of vortex reconnection events that appear during transition; (iii) study the characteristics of turbulence in the far wake, and in particular quantify the anisotropy in the flow. The initial transient dynamics is conveniently described in terms of the non-dimensional time
$h$ on the growth rates of the helical vortex instability driven by mutual inductance; (ii) characterize the type of vortex reconnection events that appear during transition; (iii) study the characteristics of turbulence in the far wake, and in particular quantify the anisotropy in the flow. The initial transient dynamics is conveniently described in terms of the non-dimensional time 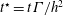 $t^{\star }=t\unicode[STIX]{x1D6E4}/h^{2}$, yielding the dimensionless growth rate of
$t^{\star }=t\unicode[STIX]{x1D6E4}/h^{2}$, yielding the dimensionless growth rate of 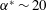 $\unicode[STIX]{x1D6FC}^{\ast }\sim 20$ and collapsing of all the LES data for a given
$\unicode[STIX]{x1D6FC}^{\ast }\sim 20$ and collapsing of all the LES data for a given 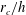 $r_{c}/h$ ratio. The vortex-core displacement growth rate is found to be Reynolds-number independent, and decreases for larger
$r_{c}/h$ ratio. The vortex-core displacement growth rate is found to be Reynolds-number independent, and decreases for larger 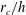 $r_{c}/h$ ratios. Several vortex reconnection events are identified during the transition, mostly initiated by the leap frogging of helical vortices. This phenomenon causes the entanglement of orthogonal vortex filaments, leading to their separation, followed by the creation of elongated threads in the axial direction. The turbulent wake generated by the breakdown of the helical vortices is found to be highly anisotropic with the axial fluctuations being dominant compared to the radial and azimuthal fluctuations (near one-dimensional turbulence). The study of integral length scales shows the presence of a strong large-scale anisotropy, retaining the memory of the initial helical pitch
$r_{c}/h$ ratios. Several vortex reconnection events are identified during the transition, mostly initiated by the leap frogging of helical vortices. This phenomenon causes the entanglement of orthogonal vortex filaments, leading to their separation, followed by the creation of elongated threads in the axial direction. The turbulent wake generated by the breakdown of the helical vortices is found to be highly anisotropic with the axial fluctuations being dominant compared to the radial and azimuthal fluctuations (near one-dimensional turbulence). The study of integral length scales shows the presence of a strong large-scale anisotropy, retaining the memory of the initial helical pitch 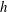 $h$, in particular for the integral scale in the axial direction. The large-scale anisotropy is propagated through the inertial and dissipative ranges, determined from the computation of the moments of velocity gradients in the three directions.
$h$, in particular for the integral scale in the axial direction. The large-scale anisotropy is propagated through the inertial and dissipative ranges, determined from the computation of the moments of velocity gradients in the three directions.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 7
- Cited by

