Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-12T22:28:26.157Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of flow over an axisymmetric body of revolution

Published online by Cambridge University Press:  23 August 2018

Praveen Kumar Open the ORCID record for Praveen Kumar [Opens in a new window]  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Praveen Kumar
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: kmahesh@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

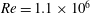Wall-resolved large-eddy simulation (LES) is used to simulate flow over an axisymmetric body of revolution at a Reynolds number, $Re=1.1\times 10^{6}$, based on the free-stream velocity and the length of the body. The geometry used in the present work is an idealized submarine hull (DARPA SUBOFF without appendages) at zero angle of pitch and yaw. The computational domain is chosen to avoid confinement effects and capture the wake up to fifteen diameters downstream of the body. The unstructured computational grid is designed to capture the fine near-wall flow structures as well as the wake evolution. LES results show good agreement with the available experimental data. The axisymmetric turbulent boundary layer has higher skin friction and higher radial decay of turbulence away from the wall, compared to a planar turbulent boundary layer under similar conditions. The mean streamwise velocity exhibits self-similarity, but the turbulent intensities are not self-similar over the length of the simulated wake, consistent with previous studies reported in the literature. The axisymmetric wake shifts from high-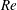$Re$ to low-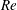$Re$ equilibrium self-similar solutions, which were only observed for axisymmetric wakes of bluff bodies in the past.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence simulation Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 537 - 563
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alin, N., Bensow, R. E., Fureby, C., Huuva, T. & Svennberg, U. 2010 Current capabilities of DES and LES for submarines at straight course. J. Ship Res. 54 (3), 184–196.Google Scholar
Babu, P. C. & Mahesh, K. 2004 Upstream entrainment in numerical simulations of spatially evolving round jets. Phys. Fluids 16 (10), 3699–3705.Google Scholar
Chase, N. & Carrica, P. M. 2013 Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Engng 60, 68–80.Google Scholar
Chase, N., Michael, T. & Carrica, P. M. 2013 Overset simulation of a submarine and propeller in towed, self-propelled and maneuvering conditions. Intl Shipbuilding Prog. 60 (1–4), 171–205.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aeronaut. Sci. 21 (2), 91–108.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3 (7), 1760.Google Scholar
Groves, N. C., Huang, T. T. & Chang, M. S. 1989 Geometric Characteristics of DARPA Suboff Models: (DTRC Model Nos. 5470 and 5471). David Taylor Research Center.Google Scholar
Huang, T., Liu, H. L., Grooves, N., Forlini, T., Blanton, J. & Gowing, S. 1992 Measurements of flows over an axisymmetric body with various appendages in a wind tunnel: the DARPA SUBOFF experimental program. In Proceedings of the 19th Symposium on Naval Hydrodynamics, Seoul, Korea. National Academy Press.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Res. Rep. CTR-S88, p. 193.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010a Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jiménez, J. M., Hultmark, M. & Smits, A. J. 2010b The intermediate wake of a body of revolution at high Reynolds numbers. J. Fluid Mech. 659, 516–539.Google Scholar
Jiménez, J. M., Reynolds, R. T. & Smits, A. J. 2010c The effects of fins on the intermediate wake of a submarine model. Trans. ASME J. Fluids Engng 132 (3), 031102.Google Scholar
Johansson, P. B. V. & George, W. K. 2006 The far downstream evolution of the high-Reynolds-number axisymmetric wake behind a disk. Part 1. Single-point statistics. J. Fluid Mech. 555, 363–385.Google Scholar
Johansson, P. B. V., George, W. K. & Gourlay, M. J. 2003 Equilibrium similarity, effects of initial conditions and local Reynolds number on the axisymmetric wake. Phys. Fluids 15 (3), 603–617.Google Scholar
Kim, S.-E., Rhee, B. J. & Miller, R. W. 2013 Anatomy of turbulent flow around DARPA SUBOFF body in a turning maneuver using high-fidelity RANS computations. Intl Shipbuilding Prog. 60 (1), 207–231.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (04), 741–773.Google Scholar
Kumar, P. & Mahesh, K. 2017 Large eddy simulation of propeller wake instabilities. J. Fluid Mech. 814, 361–396.Google Scholar
Kumar, P. & Mahesh, K. 2018 Analysis of axisymmetric boundary layers. J. Fluid Mech. 849, 927–941.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure model. Phys. Fluids A 4 (3), 633.Google Scholar
Lueptow, R. M. 1990 Turbulent boundary layer on a cylinder in axial flow. AIAA J. 28 (10), 1705–1706.Google Scholar
Luxton, R. E., Bull, M. K. & Rajagopalan, S. 1984 The thick turbulent boundary layer on a long fine cylinder in axial flow. Aeronaut. J. 88, 186–199.Google Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197 (1), 215–240.Google Scholar
Mahesh, K., Kumar, P., Gnanaskandan, A. & Nitzkorski, Z. 2015 LES applied to ship research. J. Ship Res. 59 (4), 238–245.Google Scholar
Oertel, H. Jr. 1990 Wakes behind blunt bodies. Annu. Rev. Fluid Mech. 22 (1), 539–562.Google Scholar
Park, N. & Mahesh, K. 2009 Reduction of the Germano-identity error in the dynamic Smagorinsky model. Phys. Fluids 21 (6), 065106.Google Scholar
Patel, V. C., Nakayama, A. & Damian, R. 1974 Measurements in the thick axisymmetric turbulent boundary layer near the tail of a body of revolution. J. Fluid Mech. 63 (2), 345–367.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Posa, A. & Balaras, E. 2016 A numerical investigation of the wake of an axisymmetric body with appendages. J. Fluid Mech. 792, 470–498.Google Scholar
Rotta, J.1953 On the theory of the turbulent boundary layer. NACA Tech. Mem. 1344.Google Scholar
Stella, F., Mazellier, N. & Kourta, A. 2017 Scaling of separated shear layers: an investigation of mass entrainment. J. Fluid Mech. 826, 851–887.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vaz, G., Toxopeus, S. & Holmes, S. 2010 Calculation of manoeuvring forces on submarines using two viscous-flow solvers. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China. ASME.Google Scholar
Verma, A. & Mahesh, K. 2012 A Lagrangian subgrid-scale model with dynamic estimation of Lagrangian time scale for large eddy simulation of complex flows. Phys. Fluids 24 (8), 085101.Google Scholar
Yang, C. & Löhner, R. 2003 Prediction of flows over an axisymmetric body with appendages. In The 8th International Conference on Numerical Ship Hydrodynamics, Busan, Korea.Google Scholar