Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Liao, Chuan-Chieh
and
Lin, Chao-An
2014.
Transitions of natural convection flows in a square enclosure with a heated circular cylinder.
Applied Thermal Engineering,
Vol. 72,
Issue. 1,
p.
41.
Chang, Po-Hua
Liao, Chuan-Chieh
Hsu, Hsin-Wei
Liu, Shih-Huang
and
Lin, Chao-An
2014.
Simulations of laminar and turbulent flows over periodic hills with immersed boundary method.
Computers & Fluids,
Vol. 92,
Issue. ,
p.
233.
Zhang, Hao
Trias, F. Xavier
Gorobets, Andrey
Tan, Yuanqiang
and
Oliva, Assensi
2015.
Direct numerical simulation of a fully developed turbulent square duct flow up to Reτ=1200.
International Journal of Heat and Fluid Flow,
Vol. 54,
Issue. ,
p.
258.
Liao, Chuan-Chieh
Hsiao, Wen-Wei
Lin, Ting-Yu
and
Lin, Chao-An
2015.
Simulations of two sedimenting-interacting spheres with different sizes and initial configurations using immersed boundary method.
Computational Mechanics,
Vol. 55,
Issue. 6,
p.
1191.
Owolabi, Bayode E.
and
Lin, Chao-An
2018.
Marginally turbulent Couette flow in a spanwise confined passage of square cross section.
Physics of Fluids,
Vol. 30,
Issue. 7,
Lee, You-Hsun
Huang, Li-Min
Zou, You-Seng
Huang, Shao-Ching
and
Lin, Chao-An
2018.
Simulations of turbulent duct flow with lattice Boltzmann method on GPU cluster.
Computers & Fluids,
Vol. 168,
Issue. ,
p.
14.
Chen, Sung-Hua
Ku, Yen
and
Lin, Chao-An
2019.
Simulations of settling object using moving domain and immersed-boundary method.
Computers & Fluids,
Vol. 179,
Issue. ,
p.
735.
Owolabi, Bayode
2019.
Characterisation of Turbulent Duct Flows.
p.
59.
Owolabi, Bayode
2019.
Characterisation of Turbulent Duct Flows.
p.
117.
Owolabi, Bayode
2019.
Characterisation of Turbulent Duct Flows.
p.
83.
Owolabi, Bayode
2019.
Characterisation of Turbulent Duct Flows.
p.
7.
Wu, Chung-Ming
Zhou, You-Sheng
and
Lin, Chao-An
2020.
Direct numerical simulations of turbulent channel flows with mesh-refinement lattice Boltzmann methods on GPU cluster.
Computers & Fluids,
Vol. 210,
Issue. ,
p.
104647.
Shi, Xiaolei
and
Lin, Chao-An
2020.
Simulations of Wall Bounded Turbulent Flows Using General Pressure Equation.
Flow, Turbulence and Combustion,
Vol. 105,
Issue. 1,
p.
67.
Lin, Che-Yu
and
Lin, Chao-An
2020.
Direct Numerical Simulations of Turbulent Channel Flow With Polymer Additives.
Journal of Mechanics,
Vol. 36,
Issue. 5,
p.
691.
Lin, Wei-Jie
Li, Ming-Jiun
Su, Chi-Wei
Huang, Xiao-Ying
and
Lin, Chao-An
2020.
Direct numerical simulations of turbulent periodic-hill flows with mass-conserving lattice Boltzmann method.
Physics of Fluids,
Vol. 32,
Issue. 11,
Lin, Che-Yu
Owolabi, Bayode E.
and
Lin, Chao-An
2022.
Polymer-turbulence interactions in a complex flow and implications for the drag reduction phenomenon.
Physics of Fluids,
Vol. 34,
Issue. 4,
Chiu, Tzu-Hsuan
and
Lin, Chao-An
2023.
Multigrid accelerated projection method on GPU cluster for the simulation of turbulent flows.
Journal of Mechanics,
Vol. 39,
Issue. ,
p.
199.
Sarkarinejad, Khalil
Sarkarinejad, Armin
and
Mohammadkhani, Zeynab
2024.
Fluid dynamics, structural, micro-structural, and kinematic analyses on the Kuh-e-Namak (Dashti) salt diapiric rectangular cuboid channel flow, Iran.
Marine and Petroleum Geology,
Vol. 160,
Issue. ,
p.
106625.
Jin, Bo-Xiao
Feng, Sheng-Wei
Chiu, Yi-Han
and
Lin, Chao-An
2025.
Direct Numerical Simulations of Turbulent Channel and Duct Flows Using Interpolation-Based Lattice Boltzmann Method.
Flow, Turbulence and Combustion,
Vol. 115,
Issue. 4,
p.
1445.
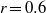 –
–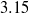 ), in a square duct at a bulk Reynolds number
), in a square duct at a bulk Reynolds number 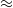 10 000 are investigated by large eddy simulation. The numerical framework consists of a finite-volume method with a staggered-grid arrangement of dependent variables. Spatial derivatives are approximated using second-order centred differencing, and a fractional-step method is used for temporal integration. Simulations are conducted with
10 000 are investigated by large eddy simulation. The numerical framework consists of a finite-volume method with a staggered-grid arrangement of dependent variables. Spatial derivatives are approximated using second-order centred differencing, and a fractional-step method is used for temporal integration. Simulations are conducted with 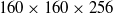 grids. Secondary flow near the Couette wall shows a gradual change of vortex size and position as the moving wall velocity increased, where the two clockwise rotating vortices gradually merge in tandem with speed of the moving wall and form a large clockwise vortex. A linear relation is observed to exist between the angle of the two vortices and the parameter
grids. Secondary flow near the Couette wall shows a gradual change of vortex size and position as the moving wall velocity increased, where the two clockwise rotating vortices gradually merge in tandem with speed of the moving wall and form a large clockwise vortex. A linear relation is observed to exist between the angle of the two vortices and the parameter  , and the angle saturates beyond
, and the angle saturates beyond 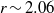 . Also, at
. Also, at 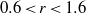 , together with a small counter-clockwise corner vortex, this vortex pattern is similar to that observed in the corner region of the duct flow with a free surface. The change of the vortex patterns also influences the dominant transport terms in the streamwise vorticity transport equation. Near the moving wall due to the reduction of the streamwise velocity fluctuation at the moving wall, turbulence structure gradually moves towards a rod-like axisymmetric turbulence, and as
, together with a small counter-clockwise corner vortex, this vortex pattern is similar to that observed in the corner region of the duct flow with a free surface. The change of the vortex patterns also influences the dominant transport terms in the streamwise vorticity transport equation. Near the moving wall due to the reduction of the streamwise velocity fluctuation at the moving wall, turbulence structure gradually moves towards a rod-like axisymmetric turbulence, and as  increases beyond
increases beyond 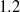 , turbulence reverts to the disc-like structure.
, turbulence reverts to the disc-like structure.
