Article contents
Large eddy simulation of transient upstream/downstream vortex interactions
Published online by Cambridge University Press: 09 January 2019
Abstract
Experimentally validated large eddy simulations were performed on two NACA0012 vanes at various lateral offsets to observe the transient effects of the near field interactions between two streamwise vortices. The vanes were separated in the streamwise direction, allowing the upstream vortex to impact on the downstream geometry. These vanes were evaluated at an angle of incidence of 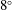 $8^{\circ }$ and a Reynolds number of 70 000, with rear vane angle reversed to create a co-rotating or counter-rotating vortex pair. The downstream vortex merged with the upstream in the co-rotating condition, driven by the suppression of one of the tip vortices of the downstream vane. At close proximity to the pressure side, the vane elongated the upstream vortex, resulting in it being the weakened and merging into the downstream vortex. This produced a transient production of bifurcated vortices in the wake region. The downstream vortex of the co-rotating pair experienced faster meandering growth, with position oscillations equalising between the vortices. The position oscillation was determined to be responsible for statistical variance in the merging location, with variation in vortex separation causing the vortices at a single plane to merge and separate in a time-dependent manner. In the counter-rotating condition position oscillations were found to be larger, with higher growth, but less uniform periodicity. It was found that the circulation transfer between the vortices was linked to the magnitude of their separation, with high separation fluctuations weakening the upstream vortex and strengthening the downstream vortex. In the case of upstream vortex impingement on the downstream vane, the upstream vortex was found to bifurcate, with a four vortex system being formed by interactions with the shear layer. This eventually resulted in a single dominant vortex, which did not magnify its oscillation amplitudes as it travelled downstream due to the destruction of the interacting vortices.
$8^{\circ }$ and a Reynolds number of 70 000, with rear vane angle reversed to create a co-rotating or counter-rotating vortex pair. The downstream vortex merged with the upstream in the co-rotating condition, driven by the suppression of one of the tip vortices of the downstream vane. At close proximity to the pressure side, the vane elongated the upstream vortex, resulting in it being the weakened and merging into the downstream vortex. This produced a transient production of bifurcated vortices in the wake region. The downstream vortex of the co-rotating pair experienced faster meandering growth, with position oscillations equalising between the vortices. The position oscillation was determined to be responsible for statistical variance in the merging location, with variation in vortex separation causing the vortices at a single plane to merge and separate in a time-dependent manner. In the counter-rotating condition position oscillations were found to be larger, with higher growth, but less uniform periodicity. It was found that the circulation transfer between the vortices was linked to the magnitude of their separation, with high separation fluctuations weakening the upstream vortex and strengthening the downstream vortex. In the case of upstream vortex impingement on the downstream vane, the upstream vortex was found to bifurcate, with a four vortex system being formed by interactions with the shear layer. This eventually resulted in a single dominant vortex, which did not magnify its oscillation amplitudes as it travelled downstream due to the destruction of the interacting vortices.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 2
- Cited by

