Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-31T05:16:42.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Kraichnan–Leith–Batchelor similarity theory and two-dimensional inverse cascades

Published online by Cambridge University Press:  18 February 2015

B. H. Burgess ,
R. K. Scott  and
T. G. Shepherd
B. H. Burgess*
Affiliation:
Department of Physics, University of Toronto, Toronto, Ontario M5S 1A7, Canada
R. K. Scott
Affiliation:
School of Mathematics and Statistics, University of St. Andrews, St. Andrews, Fife KY16 9SS, UK
T. G. Shepherd
Affiliation:
Department of Meteorology, University of Reading, Reading, Berkshire RG6 6BB, UK
*
†Email address for correspondence: belhburgess@physics.utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the scaling properties and Kraichnan–Leith–Batchelor (KLB) theory of forced inverse cascades in generalized two-dimensional (2D) fluids ( ${\it\alpha}$ -turbulence models) simulated at resolution 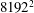$8192^{2}$ . We consider 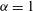${\it\alpha}=1$ (surface quasigeostrophic flow), 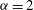${\it\alpha}=2$ (2D Euler flow) and 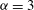${\it\alpha}=3$ . The forcing scale is well resolved, a direct cascade is present and there is no large-scale dissipation. Coherent vortices spanning a range of sizes, most larger than the forcing scale, are present for both 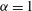${\it\alpha}=1$ and 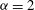${\it\alpha}=2$ . The active scalar field for 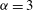${\it\alpha}=3$ contains comparatively few and small vortices. The energy spectral slopes in the inverse cascade are steeper than the KLB prediction 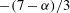$-(7-{\it\alpha})/3$ in all three systems. Since we stop the simulations well before the cascades have reached the domain scale, vortex formation and spectral steepening are not due to condensation effects; nor are they caused by large-scale dissipation, which is absent. One- and two-point p.d.f.s, hyperflatness factors and structure functions indicate that the inverse cascades are intermittent and non-Gaussian over much of the inertial range for 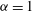${\it\alpha}=1$ and 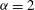${\it\alpha}=2$ , while the 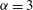${\it\alpha}=3$ inverse cascade is much closer to Gaussian and non-intermittent. For 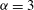${\it\alpha}=3$ the steep spectrum is close to that associated with enstrophy equipartition. Continuous wavelet analysis shows approximate KLB scaling 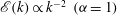$\mathscr{E}(k)\propto k^{-2}~({\it\alpha}=1)$ and 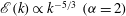$\mathscr{E}(k)\propto k^{-5/3}~({\it\alpha}=2)$ in the interstitial regions between the coherent vortices. Our results demonstrate that coherent vortex formation ( 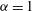${\it\alpha}=1$ and 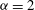${\it\alpha}=2$ ) and non-realizability ( 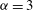${\it\alpha}=3$ ) cause 2D inverse cascades to deviate from the KLB predictions, but that the flow between the vortices exhibits KLB scaling and non-intermittent statistics for 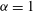${\it\alpha}=1$ and 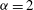${\it\alpha}=2$ .

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence simulation

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 467 - 496
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alvelius, K. 1999 Random forcing of three-dimensional homogeneous turbulence. Phys. Fluids 11, 1880–1889.Google Scholar
Azzalini, A., Farge, M. & Schneider, K. 2005 Nonlinear wavelet thresholding: a recursive method to determine the optimal denoising threshold. Appl. Comput. Harmon. Anal. 18, 177–185.CrossRefGoogle Scholar
Babiano, A., Basdevant, C., Legras, B. & Sadourny, R. 1987 Vorticity and passive-scalar dynamics in two-dimensional turbulence. J. Fluid Mech. 183, 379–397.Google Scholar
Babiano, A., Dubrulle, B. & Frick, P. 1995 Scaling properties of numerical two-dimensional turbulence. Phys. Rev. E 4, 3719–3729.Google Scholar
Bartello, P. & Warn, T. 1996 Self-similarity of decaying two-dimensional turbulence. J. Fluid Mech. 326, 357–372.Google Scholar
Basdevant, C., Legras, B. & Sadourny, R. 1981 A study of barotropic model flows: intermittency, waves, and predictability. J. Atmos. Sci. 38, 2305–2326.2.0.CO;2>CrossRefGoogle Scholar
Basdevant, C. & Philipovitch, T. 1994 On the validity of the Weiss criterion in two-dimensional turbulence. Physica D 73, 17–30.CrossRefGoogle Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids Suppl. 12 (II), 233–239.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29–R32.CrossRefGoogle ScholarPubMed
Benzi, R., Paladin, G., Patarnello, S., Santangelo, P. & Vulpiani, A. 1986 Intermittency and coherent structures in two-dimensional turbulence. J. Phys. A: Math. Gen. 19, 3771–3784.Google Scholar
Beta, C., Schneider, K. & Farge, M. 2004 Mixing in two-dimensional isotropic turbulence: a numerical study using orthogonal wavelet filtering. Adv. Turbul. 10, 271–274.Google Scholar
Boffetta, G. 2007 Energy and enstrophy fluxes in the double cascade of two-dimensional turbulence. J. Fluid Mech. 589, 253–260.CrossRefGoogle Scholar
Boffetta, G., Celani, A. & Vergassola, M. 2000 Inverse cascade in two-dimensional turbulence: deviations from Gaussian behaviour. Phys. Rev. E 61, R29–R32.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.CrossRefGoogle Scholar
Borue, V. 1994 Inverse energy cascade in stationary two-dimensional homogeneous turbulence. Phys. Rev. Lett. 72, 1475–1478.Google Scholar
Bos, W. J. T. & Bertoglio, J.-P. 2009 Large-scale bottleneck effect in two-dimensional turbulence. J. Turbul. 10, 1–8.Google Scholar
Bruneau, C. H. & Kellay, H. 2005 Experiments and direct numerical simulations of two-dimensional turbulence. Phys. Rev. E 71, 046305.Google Scholar
Burgess, B. H.2014 The applicability of Kraichnan–Leith–Batchelor similarity theory to inverse cascades in generalized two-dimensional turbulence. PhD thesis, University of Toronto.CrossRefGoogle Scholar
Burgess, B. H. & Shepherd, T. G. 2013 Spectral non-locality, absolute equilibria, and Kraichnan–Leith–Batchelor phenomenology in two-dimensional turbulent energy cascades. J. Fluid Mech. 725, 332–371.Google Scholar
Danilov, S. & Gurarie, D. 2001 Nonuniversal features of forced two-dimensional turbulence in the energy range. Phys. Rev. E 63, 020203.Google Scholar
Daubechies, I. 1992 Ten Lectures on Wavelets, CBMS Lecture Note Series. SIAM.CrossRefGoogle Scholar
Davidson, P. 2004 Turbulence: An Introduction for Scientists and Engineers. Cambridge University Press.Google Scholar
Do-Khac, M., Basdevant, C., Perrier, V. & Dang-Tran, K. 1994 Wavelet analysis of 2D turbulent fields. Physica D 76, 252–277.CrossRefGoogle Scholar
Dubos, T., Babiano, A., Paret, J. & Tabeling, P. 2001 Intermittency and coherent structures in the two-dimensional inverse energy cascade: comparing numerical and laboratory experiments. Phys. Rev. E 64, 036302.Google Scholar
Dubrulle, B. 1994 Intermittency in fully developed turbulence: log-Poisson statistics and generalized scale covariance. Phys. Rev. Lett. 7, 959–962.Google Scholar
Elhmaidi, D. 2005 Large-scale dissipation and filament instability in two-dimensional turbulence. Phys. Rev. Lett. 95, 014503.Google Scholar
Farazmand, M. M., Kevlahan, N. K.-R. & Protas, B. 2011 Controlling the dual cascade of two-dimensional turbulence. J. Fluid Mech. 668, 202–222.Google Scholar
Farge, M., Guezennec, Y., Ho, C. M. & Meneveau, C.1990 Continuous wavelet analysis of coherent structures. In Proceedings of the Summer Prog. Cent. Turbulence Res., Stanford Univ. NASA-Ames, Stanford, CA.Google Scholar
Farge, M., Schneider, K. & Kevlahan, N. 1999 Non-Gaussianity and coherent vortex simulation for two-dimensional turbulence using an adaptive orthogonal wavelet basis. Phys. Fluids 11, 2187–2201.Google Scholar
Fontane, J., Dritschel, D. G. & Scott, R. K. 2013 Vortical control of forced two-dimensional turbulence. Phys. Fluids 25, 015101.Google Scholar
Frisch, U. & Sulem, P. L. 1984 Numerical simulation of the inverse cascade in two-dimensional turbulence. Phys. Fluids 27, 1921–1923.CrossRefGoogle Scholar
Germano, M. 1992 Turbulence: the filtering approach. J. Fluid Mech. 238, 325–336.CrossRefGoogle Scholar
Hasegawa, A. & Mima, K. 1978 Pseudo-three-dimensional turbulence in a magnetized nonuniform plasma. Phys. Fluids 21, 87–92.Google Scholar
Held, I. M., Pierrehumbert, R. T., Garner, S. T. & Swanson, K. L. 1995 Surface quasi-geostrophic dynamics. J. Fluid Mech. 282, 1–20.Google Scholar
Herring, J. R. & McWilliams, J. C. 1985 Comparison of direct numerical simulation of two-dimensional turbulence with two-point closure: the effects of intermittency. J. Fluid Mech. 153, 229–242.Google Scholar
Hou, T. Y. & Li, R. 2006 Dynamic depletion of vortex stretching and non-blowup of the 3-D incompressible Euler equations. J. Nonlinear Sci. 16, 639–664.Google Scholar
Hua, B. L. & Lein, P. 1998 An exact criterion for the stirring properties of nearly two-dimensional turbulence. Physica D 113, 98–110.Google Scholar
Iwayama, T. & Watanabe, T. 2010 Green’s function for a generalized two-dimensional fluid. Phys. Rev. E 82, 036307.Google Scholar
Iwayama, T. & Watanabe, T. 2014 Universal spectrum in the infrared range of two-dimensional turbulent flows. Phys. Fluids 26, 025105.Google Scholar
Kevlahan, N. & Farge, M. 1997 Vorticity filaments in two-dimensional turbulence: creation, stability, and effect. J. Fluid Mech. 346, 49–76.Google Scholar
Kirby, J. 2005 Which wavelet best reproduces the Fourier power spectrum? Comput. Geosci. 31, 846–864.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
Kraichnan, R. H. 1971 Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.CrossRefGoogle Scholar
Leith, C. E. 1968 Diffusion approximation for two-dimensional turbulence. Phys. Fluids 11, 671–673.Google Scholar
Maltrud, M. E. & Vallis, G. K. 1991 Energy spectra and coherent structures in forced two-dimensional and beta-plane turbulence. J. Fluid Mech. 228, 321–342.Google Scholar
McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.Google Scholar
McWilliams, J. C. 1990 The vortices of two-dimensional turbulence. J. Fluid Mech. 219, 361–385.Google Scholar
Mizuta, A., Matsumoto, T. & Toh, S. 2013 Transition of the scaling law in inverse energy cascade range caused by a nonlocal excitation of coherent structures observed in two-dimensional turbulent fields. Phys. Rev. E 88, 053009.Google Scholar
Ohkitani, K. 1991 Wavenumber space dynamics of enstrophy cascade in a forced two-dimensional turbulence. Phys. Fluids 3, 1598–1611.Google Scholar
Paret, J. & Tabeling, P. 1998 Intermittency in the two-dimensional inverse cascade of energy: experimental observations. Phys. Fluids 10, 3126–3136.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Pierrehumbert, R. T., Held, I. M. & Swanson, K. L. 1994 Spectra of local and nonlocal two-dimensional turbulence. Chaos, Solitons Fractals 4, 1111–1116.CrossRefGoogle Scholar
Pouquet, A., Lesieur, M., Andre, J. C. & Basdevant, C. 1975 Evolution of high Reynolds number two-dimensional turbulence. J. Fluid Mech. 72, 305–319.Google Scholar
Rutgers, M. 1998 Forced 2D turbulence: experimental evidence of simultaneous inverse energy and forward enstrophy cascades. Phys. Rev. Lett. 11, 2244–2247.Google Scholar
Santangelo, P., Benzi, R. & Legras, B. 1989 The generation of vortices in high-resolution, two-dimensional decaying turbulence and the influence of initial conditions on the breaking of self-similarity. Phys. Fluids A 1, 1027–1034.Google Scholar
Schorghofer, N. 2000 Universality of probability distributions among two-dimensional turbulent flows. Phys. Rev. E 61, 6568–6571.Google Scholar
Scott, R. K. 2007 Nonrobustness of the two-dimensional turbulent inverse cascade. Phys. Rev. E 75, 046301.Google Scholar
Smith, K. S., Boccaletti, G., Henning, C. C., Marinov, I., Tam, C. Y., Held, I. M. & Vallis, G. K. 2002 Turbulent diffusion in the geostrophic inverse cascade. J. Fluid Mech. 469, 13–48.Google Scholar
Smith, L. M. & Yakhot, V. 1994 Finite-size effects in forced two-dimensional turbulence. J. Fluid Mech. 274, 115–138.Google Scholar
Sommeria, J. 1986 Experimental study of the two-dimensional inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.Google Scholar
Vallgren, A. 2011 Infrared Reynolds number dependency of two-dimensional inverse energy cascade. J. Fluid Mech. 667, 463–473.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Watanabe, T. & Iwayama, T. 2004 Unified scaling theory for local and non-local transfers in generalized two-dimensional turbulence. J. Phys. Soc. Japan 12, 3319–3330.Google Scholar