Hostname: page-component-5b777bbd6c-vfh8q Total loading time: 0 Render date: 2025-06-25T16:34:50.050Z Has data issue: false hasContentIssue false
  • English
  • Français

Jump of an atomic force microscopy probe towards an elastic substrate in a liquid environment

Published online by Cambridge University Press:  24 June 2025

Zhaohe Dai Open the ORCID record for Zhaohe Dai [Opens in a new window]
Zhaohe Dai*
Affiliation:
Department of Mechanics and Engineering Science, State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, PR China
*
Corresponding author: Zhaohe Dai, daizh@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

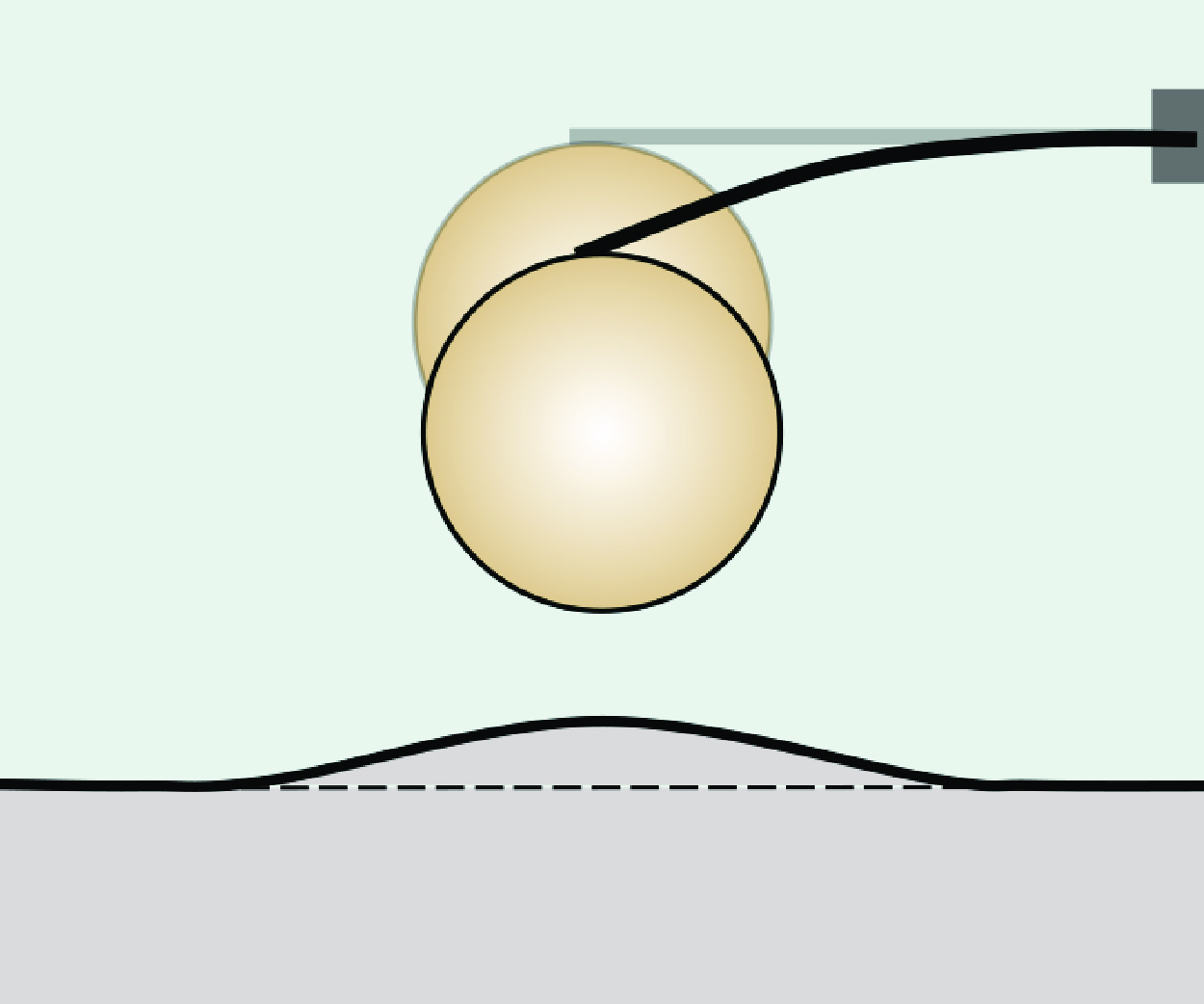
In typical atomic force microscopy (AFM) measurements, the AFM probe, mounted on a compliant cantilever, is brought into close proximity to the test substrate. At this range, interfacial attractive van der Waals (vdW) forces can deflect the cantilever by pulling the probe, often causing the probe to suddenly jump into contact with the substrate. For deformable substrates such as gels or bio-tissues, the attraction-induced substrate deformation can further reduce the gap beneath the probe, which can increase the vdW force and hence trigger jump-to-contact prematurely. Since soft gels and tissues are frequently tested in liquid environments, where surface tension and the approaching dynamics of the probe can significantly influence deformation behaviour, this study examines the statics and dynamics of jump-to-contact on elastic substrates incorporating the effect of solid surface tension. We first discuss the theoretical setting for the static problem, deriving perturbation solutions for limiting cases of small and large solid surface tension. Notably, even under conditions of large solid surface tension, elasticity remains critical, as far-field elastic forces are required to smooth surface deformations in a convergent manner. Recognising that practical experiments are inherently dynamic, we also analyse the role of hydrodynamic pressure, which can delay the premature jump-to-contact. Our analysis focuses on identifying the conditions under which dynamic effects are negligible, enabling the simple analytical solutions in the static problem to reliably interpret AFM experimental results.

JFM classification

Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1013 , 25 June 2025 , A49
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andreotti, B. & Snoeijer, J.H. 2020 Statics and dynamics of soft wetting. Annu. Rev. Fluid Mech. 52 (1), 285–308.10.1146/annurev-fluid-010719-060147CrossRefGoogle Scholar
Baró, A.M. & Reifenberger, R.G. 2012 Atomic Force Microscopy in Liquid: Biological Applications. John Wiley & Sons.10.1002/9783527649808CrossRefGoogle Scholar
Bateman, H. & Erdélyi, A. 1953 Higher Transcendental Functions, vol. I. (Bateman Manuscript Project). McGraw-Hill Book Company, Inc.Google Scholar
Beaty, E. & Lister, J.R. 2023 Inertial and viscous dynamics of jump-to-contact between fluid drops under van der Waals attraction. J. Fluid Mech. 957, A25.10.1017/jfm.2023.71CrossRefGoogle Scholar
Bertin, V. 2024 Similarity solutions in elastohydrodynamic bouncing. J. Fluid Mech. 986, A13.10.1017/jfm.2024.310CrossRefGoogle Scholar
Bertin, V., Amarouchene, Y., Raphaël, E. & Salez, T. 2022 Soft-lubrication interactions between a rigid sphere and an elastic wall. J. Fluid Mech. 933, A23.10.1017/jfm.2021.1063CrossRefGoogle Scholar
Bertin, V., Oratis, A. & Snoeijer, J.H. 2025 Sticking without contact: elastohydrodynamic adhesion. Phys. Rev. X 15 (2), 021006.Google Scholar
Bico, J., Reyssat, É. & Roman, B. 2018 Elastocapillarity: when surface tension deforms elastic solids. Annu. Rev. Fluid Mech. 50 (1), 629–659.10.1146/annurev-fluid-122316-050130CrossRefGoogle Scholar
Binnig, G., Quate, C.F. & Gerber, C. 1986 Atomic force microscope. Phys. Rev. Lett. 56 (9), 930–933.10.1103/PhysRevLett.56.930CrossRefGoogle ScholarPubMed
Box, F., Jacquemot, C., Adda-Bedia, M. & Vella, D. 2020 Cloaking by coating: how effectively does a thin, stiff coating hide a soft substrate? Soft Matt. 16 (19), 4574–4583.10.1039/C9SM02511ACrossRefGoogle ScholarPubMed
Chandler, T.G.J. & Vella, D. 2020 Validity of Winkler’s mattress model for thin elastomeric layers: beyond Poisson’s ratio. Proc. R. Soc. Lond. A 476 (2242), 20200551.Google ScholarPubMed
Chen, X., Li, B., Liao, Z., Li, J., Li, X., Yin, J. & Guo, W. 2022 Principles and applications of liquid‐environment atomic force microscopy. Adv. Mater. Interfaces 9 (35), 2201864.10.1002/admi.202201864CrossRefGoogle Scholar
Chireux, V., Protat, M., Risso, F., Ondarçuhu, T. & Tordjeman, P. 2018 Jump-to-contact instability: the nanoscale mechanism of droplet coalescence in air. Phys. Rev. Fluids 3 (10), 102001.10.1103/PhysRevFluids.3.102001CrossRefGoogle Scholar
Ciavarella, M., Greenwood, J.A. & Barber, J.R. 2017 Effect of Tabor parameter on hysteresis losses during adhesive contact. J. Mech. Phys. Solids 98, 236–244.10.1016/j.jmps.2016.10.005CrossRefGoogle Scholar
Ciavarella, M., Joe, J., Papangelo, A. & Barber, J.R. 2019 The role of adhesion in contact mechanics. J. R. Soc. Interface 16 (151), 20180738.10.1098/rsif.2018.0738CrossRefGoogle ScholarPubMed
Daddi-Moussa-Ider, A., Rallabandi, B., Gekle, S., Stone, H.A. 2018 Reciprocal theorem for the prediction of the normal force induced on a particle translating parallel to an elastic membrane. Phys. Rev. Fluids 3 (8), 084101.10.1103/PhysRevFluids.3.084101CrossRefGoogle Scholar
Dai, Z., Liu, L., Zhang, Z. 2019 Strain engineering of 2D materials: issues and opportunities at the interface. Adv. Mater. 31 (45), 1805417.10.1002/adma.201805417CrossRefGoogle Scholar
Dai, Z., Lu, N., Liechti, K.M. & Huang, R. 2020 Mechanics at the interfaces of 2D materials: challenges and opportunities. Curr. Opin. Solid State Mater. Sci. 24 (4), 100837.10.1016/j.cossms.2020.100837CrossRefGoogle Scholar
Dai, Z. & Vella, D. 2022 Droplets on lubricated surfaces: the slow dynamics of skirt formation. Phys. Rev. Fluids 7 (5), 054003.10.1103/PhysRevFluids.7.054003CrossRefGoogle Scholar
Davis, R.H., Serayssol, J.-M. & Hinch, E.J. 1986 The elastohydrodynamic collision of two spheres. J. Fluid Mech. 163, 479–497.10.1017/S0022112086002392CrossRefGoogle Scholar
Essink, M.H., Pandey, A., Karpitschka, S., Venner, C.H. & Snoeijer, J.H. 2021 Regimes of soft lubrication. J. Fluid Mech. 915, A49.10.1017/jfm.2021.96CrossRefGoogle ScholarPubMed
Feng, J.Q. 2000 Contact behavior of spherical elastic particles: a computational study of particle adhesion and deformations. Colloids Surf. A: Physicochem. Engng Aspects 172 (1–3), 175–198.10.1016/S0927-7757(00)00580-XCrossRefGoogle Scholar
French, R.H. et al. 2010 Long range interactions in nanoscale science. Rev. Mod. Phys. 82 (2), 1887–1944.10.1103/RevModPhys.82.1887CrossRefGoogle Scholar
Friedrichs, J., Helenius, J. & Muller, D.J. 2010 Quantifying cellular adhesion to extracellular matrix components by single-cell force spectroscopy. Nat. Protoc. 5 (7), 1353–1361.10.1038/nprot.2010.89CrossRefGoogle ScholarPubMed
Gomez, M., Moulton, D.E. & Vella, D. 2017 a Critical slowing down in purely elastic ‘snap-through’ instabilities. Nat. Phys. 13 (2), 142–145.10.1038/nphys3915CrossRefGoogle Scholar
Gomez, M., Moulton, D.E. & Vella, D. 2017 b Delayed pull-in transitions in overdamped MEMS devices. J. Micromech. Microengng 28 (1), 015006.10.1088/1361-6439/aa9a70CrossRefGoogle Scholar
Greenwood, J.A. 1997 Adhesion of elastic spheres, Proc. R. Soc. Lond A: Math. Phys. Engng Sci. 453 (1961), 1277–1297.10.1098/rspa.1997.0070CrossRefGoogle Scholar
Hamaker, H.C. 1937 The London–van der Waals attraction between spherical particles. Physica 4 (10), 1058–1072.10.1016/S0031-8914(37)80203-7CrossRefGoogle Scholar
Hannah, M. 1951 Contact stress and deformation in a thin elastic layer. Q. J. Mech. Appl. Maths 4 (1), 94–105.10.1093/qjmam/4.1.94CrossRefGoogle Scholar
Israelachvili, J.N. 2011 Intermolecular and Surface Forces. Academic Press.Google Scholar
Israelachvili, J.N. & Tabor, D. 1972 The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proc. R. Soc. Lond. A: Math. Phys. Sci. 331, 19–38.Google Scholar
Jha, A., Amarouchene, Y. & Salez, T. 2024 Capillary lubrication of a spherical particle near a fluid interface. J. Fluid Mech. 1001, A58.10.1017/jfm.2024.1158CrossRefGoogle Scholar
Johnson, K.L. & Greenwood, J.A. 1997 An adhesion map for the contact of elastic spheres. J. Colloid Interface Sci. 192 (2), 326–333.10.1006/jcis.1997.4984CrossRefGoogle ScholarPubMed
Juel, A., Pihler-Puzović, D. & Heil, M. 2018 Instabilities in blistering. Annu. Rev. Fluid Mech. 50 (1), 691–714.10.1146/annurev-fluid-122316-045106CrossRefGoogle Scholar
Krichen, S., Liu, L. & Sharma, P. 2019 Liquid inclusions in soft materials: capillary effect, mechanical stiffening and enhanced electromechanical response. J. Mech. Phys. Solids 127, 332–357.10.1016/j.jmps.2019.03.010CrossRefGoogle Scholar
Krieg, M., Fläschner, G., Alsteens, D., Gaub, B.M., Roos, W.H., Wuite, G.J.L., Gaub, H.E., Gerber, C., Dufrêne, Y.F. & Müller, D.J. 2019 Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 1 (1), 41–57.10.1038/s42254-018-0001-7CrossRefGoogle Scholar
Leal, L.G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.10.1017/CBO9780511800245CrossRefGoogle Scholar
Ledesma-Alonso, R., Legendre, D. & Tordjeman, P. 2012 Nanoscale deformation of a liquid surface. Phys. Rev. Lett. 108 (10), 106104.10.1103/PhysRevLett.108.106104CrossRefGoogle ScholarPubMed
Li, H., Yu, C. & Dai, Z. 2024 Regimes in the axisymmetric stiction of thin elastic plates. Intl J. Mech. Sci. 284, 109740.10.1016/j.ijmecsci.2024.109740CrossRefGoogle Scholar
Liu, N., Bai, Y.-L., Xia, M.-F. & Ke, F.-J. 2005 Combined effect of surface tension, gravity and van der Waals force induced by a non-contact probe tip on the shape of liquid surface. Chin. Phys. Lett. 22 (8), 2012–2015.Google Scholar
Liu, M., Gomez, M. & Vella, D. 2021 Delayed bifurcation in elastic snap-through instabilities. J. Mech. Phys. Solids 151, 104386.10.1016/j.jmps.2021.104386CrossRefGoogle Scholar
Mortagne, C., Chireux, V., Ledesma-Alonso, R., Ogier, M., Risso, F., Ondarçuhu, T., Legendre, D. & Tordjeman, P. 2017 Near-field deformation of a liquid interface by atomic force microscopy. Phys. Rev. E 96 (1), 012802.10.1103/PhysRevE.96.012802CrossRefGoogle ScholarPubMed
Poulain, S. & Carlson, A. 2022 Droplet settling on solids coated with a soft layer. J. Fluid Mech. 934, A25.10.1017/jfm.2021.1112CrossRefGoogle Scholar
Press, W.H., Teukolsky, S.A., Vetterling, W.T. & Flannery, B.P. 2007 Numerical Recipes 3rd Edition: The Art of Scientific Computing. Cambridge University Press.Google Scholar
Quinn, D.B., Feng, J. & Stone, H.A. 2013 Analytical model for the deformation of a fluid–fluid interface beneath an AFM probe. Langmuir 29 (5), 1427–1434.10.1021/la304359hCrossRefGoogle ScholarPubMed
Rallabandi, B. 2024 Fluid–elastic interactions near contact at low Reynolds number. Annu. Rev. Fluid Mech. 56 (1), 491–519.10.1146/annurev-fluid-120720-024426CrossRefGoogle Scholar
Sneddon, I.N. 1995 Fourier Transforms. Courier Corporation.Google Scholar
Style, R.W., Jagota, A., Hui, C.-Y. & Dufresne, E.R. 2017 Elastocapillarity: surface tension and the mechanics of soft solids. Annu. Rev. Condens. Matt. Phys. 8 (1), 99–118.10.1146/annurev-conmatphys-031016-025326CrossRefGoogle Scholar
Tabor, D. & Winterton, R.H.S. 1969 The direct measurement of normal and retarded van der Waals forces. Proc. R. Soc. Lond. A: Math. Phys. Sci. 312 (1511), 435–450.Google Scholar
Tavakol, B., Froehlicher, G., Holmes, D.P. & Stone, H.A. 2017 Extended lubrication theory: improved estimates of flow in channels with variable geometry. Proc. R. Soc. Lond. A 473 (2206), 20170234.Google ScholarPubMed
Tomlinson, G.A. 1928 LXVII. Molecular cohesion. Lond. Edinb. Dublin Phil. Mag. J. Sci. 6 (37), 695–712.10.1080/14786441008564646CrossRefGoogle Scholar
Viljoen, A., Mathelié-Guinlet, M., Ray, A., Strohmeyer, N., Oh, Y.J., Hinterdorfer, P., Müller, D.J., Alsteens, D. & Dufrêne, Y.F. 2021 Force spectroscopy of single cells using atomic force microscopy. Nat. Rev. Meth. Prim. 1 (1), 63.10.1038/s43586-021-00062-xCrossRefGoogle Scholar
Wang, Y., Feng, Z. & Frechette, J. 2020 Dynamic adhesion due to fluid infusion. Curr. Opin. Colloid Interface Sci. 50, 101397.10.1016/j.cocis.2020.101397CrossRefGoogle Scholar
Wegmann, S., Medalsy, I.D., Mandelkow, E. & Müller, D.J. 2013 The fuzzy coat of pathological human Tau fibrils is a two-layered polyelectrolyte brush. Proc. Natl Acad. Sci. USA 110 (4), E313–E321.10.1073/pnas.1212100110CrossRefGoogle ScholarPubMed
Wu, J.-J. 2010 The jump-to-contact distance in atomic force microscopy measurement. J. Adhes. 86 (11), 1071–1085.10.1080/00218464.2010.519256CrossRefGoogle Scholar
Yu, C. & Dai, Z. 2024 Premature jump-to-contact with elastic surfaces. J. Mech. Phys. Solids 193, 105919.10.1016/j.jmps.2024.105919CrossRefGoogle Scholar
Yu, C., Zeng, W., Wang, B., Cui, X., Gao, Z., Yin, J., Liu, L., Wei, X., Wei, Y. & Dai, Z. 2025 Stiffer is stickier: adhesion in elastic nanofilms. Nano Lett. 25 (5), 1876–1882.10.1021/acs.nanolett.4c05309CrossRefGoogle ScholarPubMed
Zhang, Z., Bertin, V., Arshad, M., Raphaël, E., Salez, T. & Maali, A. 2020 Direct measurement of the elastohydrodynamic lift force at the nanoscale. Phys. Rev. Lett. 124 (5), 054502.10.1103/PhysRevLett.124.054502CrossRefGoogle ScholarPubMed
Zhang, Z., Bertin, V., Essink, M.H., Zhang, H., Fares, N., Shen, Z., Bickel, T., Salez, T. & Maali, A. 2023 Unsteady drag force on an immersed sphere oscillating near a wall. J. Fluid Mech. 977, A21.10.1017/jfm.2023.987CrossRefGoogle Scholar
Zheng, W. & Dai, Z. 2025 Universal pull-off force for separating a rigid sphere from a membrane. J. Mech. Phys. Solids 201, 106163.10.1016/j.jmps.2025.106163CrossRefGoogle Scholar
Zheng, Z., Griffiths, I.M. & Stone, H.A. 2015 Propagation of a viscous thin film over an elastic membrane. J. Fluid Mech. 784, 443–464.10.1017/jfm.2015.598CrossRefGoogle Scholar
Zhu, Y., Ni, Y., Huang, C., Yu, J., Yao, H. & Zheng, Z. 2025 Unified model for adhesive contact between solid surfaces at micro/nano-scale. J. Mech. Phys. Solids 196, 106004.10.1016/j.jmps.2024.106004CrossRefGoogle Scholar