Article contents
Jetting in finite-amplitude, free, capillary-gravity waves
Published online by Cambridge University Press: 17 December 2020
Abstract
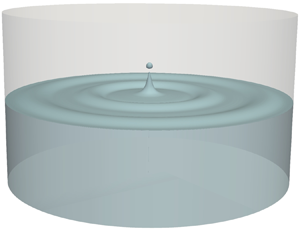
We present a theoretical and computational study of the mechanics of a jet formed from a large amplitude, axisymmetric, capillary-gravity wave on the surface of a liquid pool in a cylindrical container. Jetting can cause a pronounced overshoot of the interface at the axis of symmetry. A linear theory presented earlier in Farsoiya et al. (J. Fluid Mech., vol. 826, 2017, pp. 797–818) was shown to be incapable of describing this jet. To understand its mechanics, we present here the inviscid, weakly nonlinear solution to the initial value problem where the initial surface perturbation is a single Fourier–Bessel mode on quiescent fluid. The theory predicts that energy injected into a primary (Bessel) mode initially is transferred nonlinearly to a spectrum of modes. The extent of the theoretically predicted energy transfer is found to be very accurate for modes up to the second harmonic. We show using numerical simulations that the jet originates as a small dimple formed at the trough of the wave, analogous to similar observations in bubble cavity collapse (Duchemin et al., Phys. Fluids, vol. 14, 2002, pp. 3000–3008; Lai et al., Phys. Rev. Lett. vol. 121, 2018, 144501). The theory is able to describe the jet overshoot and the velocity and pressure fields in the liquid qualitatively, but does not capture the temporal evolution of the dimple or the thinning of the jet neck leading to pinchoff. Modal analysis shows that the latter phenomenon requires higher-order approximations, beyond the second order presented here. The nonlinear theory yields explicit analytical expressions without any fitting parameters which are systematically tested against numerical simulations of the incompressible Euler equation. The theory contains cylindrical analogues of the singularities corresponding to second harmonic resonance (Wilton, Lond. Edinb. Dubl. Phil. Mag. J. Sci., vol. 29, 1915, pp. 688–700). The connection of these to triadic resonant interactions among capillary-gravity waves in a cylindrical confined geometry is discussed.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by


