Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T06:03:20.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Jettable fluid space and jetting characteristics of a microprint head

Published online by Cambridge University Press:  23 October 2012

Loke-Yuen Wong ,
Guan-Hui Lim ,
Thiha Ye ,
F. B. Shanjeera Silva ,
Jing-Mei Zhuo ,
Rui-Qi Png ,
Soo-Jin Chua  and
Peter K. H. Ho
Loke-Yuen Wong
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
Guan-Hui Lim
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore Department of Electrical and Computer Engineering, National University of Singapore, Lower Kent Ridge Road, Singapore 117576, Republic of Singapore
Thiha Ye
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
F. B. Shanjeera Silva
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
Jing-Mei Zhuo
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
Rui-Qi Png
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
Soo-Jin Chua
Affiliation:
Department of Electrical and Computer Engineering, National University of Singapore, Lower Kent Ridge Road, Singapore 117576, Republic of Singapore
Peter K. H. Ho*
Affiliation:
Department of Physics, National University of Singapore, Lower Kent Ridge Road, Singapore 117542, Republic of Singapore
*
†Email address for correspondence: phyhop@nus.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of fluid droplet properties on the droplet-on-demand jetting of a Newtonian model fluid (water–isopropanol–ethylene glycol ternary system) has been studied. The composition of the fluid was adjusted to investigate how the Ohnesorge number ( 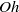$\mathit{Oh}$ ) influences droplet formation (morphology and speed) by a microfabricated short-channel shear-mode piezoelectric transducer. The fluid space for satellite-free single droplet formation was indeed found to be bound by upper and lower 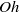$\mathit{Oh}$ limits, but these shift approximately linearly with the piezo pulse voltage amplitude 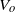${V}_{o} $ , which has a stronger influence on jetting characteristics than pulse length. Therefore the jettable fluid space can be depicted on a 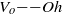${V}_{o} {{\ndash}}\mathit{Oh}$ diagram. Satellite-free droplets of the model fluid can be jetted over a wide 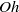$\mathit{Oh}$ range, at least 0.025 to 0.5 (corresponding to 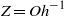$Z= {\mathit{Oh}}^{\ensuremath{-} 1} $ of 40 to 2), by adjusting 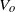${V}_{o} $ appropriately. Air drag was found to dominate droplet flight, as may be expected. This can be accurately modelled to yield droplet formation time, which turned out to be 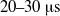$20\text{{\ndash}} 30~\lrm{\ensuremath{\mu}} \mathrm{s} $ under a wide range of jetting conditions. The corresponding initial droplet speed was found to vary linearly with 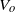${V}_{o} $ , with a fluid-dependent threshold but a fluid-independent slope, and a minimum speed of about 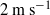$2~\mathrm{m} ~{\mathrm{s} }^{\ensuremath{-} 1} $ . This suggests the existence of iso-velocity lines that run substantially parallel to the lower jetting boundary in the 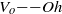${V}_{o} {{\ndash}}\mathit{Oh}$ diagram.

JFM classification

Drops and Bubbles: Drops Drops and Bubbles: Drops and Bubbles Materials Processing Flows: Materials Processing Flows Materials Processing Flows: Microelectronics

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 713 , 25 December 2012 , pp. 109 - 122
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, F. F. 1970 Functional dependence of drag coefficient of a sphere on Reynolds number. Phys. Fluids 13, 2194–2195.Google Scholar
Aernouts, T., Aleksandrov, T., Girotto, C., Genoe, J. & Poortmans, J. 2008 Polymer based organic solar cells using ink-jet printed active layers. Appl. Phys. Lett. 92, 033306.Google Scholar
Anto, B. T., Sivaramakrishnan, S., Chua, L. L. & Ho, P. K. H. 2010 Hydrophilic sparse ionic monolayer-protected metal nanoparticles: highly concentrated nano-Au and nano-Ag ‘inks’ that can be sintered to near-bulk conductivity at $150\hspace{0.167em} \textdegree \mathrm{C} $ . Adv. Funct. Mater. 20, 296–303.Google Scholar
Arias, A. C., Ready, S. E., Lujan, R., Wong, W. S., Paul, K. E., Salleo, A., Chabinyc, M. L., Apte, R., Street, R. A., Wu, Y., Liu, P. & Ong, B. 2004 All jet-printed polymer thin-film transistor active-matrix backplanes. Appl. Phys. Lett. 85, 3304–3306.CrossRefGoogle Scholar
Bale, M., Carter, J. C., Creighton, C. J., Gregory, H. J., Lyon, P. H., Ng, P., Webb, L. & Wehrum, A. 2006 Ink-jet printing: the route to production of full colour P-OLED displays. J. Soc. Info. Displ. 453–459.Google Scholar
Berggren, M., Nilsson, D. & Robinson, N. D. 2006 Organic materials for printed electronics. Nature Mater. 6, 3–5.CrossRefGoogle Scholar
Bibl, A., Chen, Z. & Birkmeyer, J. 2005 Print head with thin membrane. Patent (U.S.P.T.O.), 0099467.Google Scholar
Czyzewski, J., Burzynski, P., Gawel, K. & Meisner, J. 2009 Rapid prototyping of electrically conductive components using 3D printing technology. J. Mater. Process. Technol. 209, 5281–5285.Google Scholar
Dearden, A. L., Smith, P. J., Shin, D.-Y., Reis, N., Derby, B. & O’Brien, P. 2005 A low curing temperature silver ink for use in inkjet printing and subsequent production of conductive tracks. Macromol. Rapid Commun. 26, 315–318.CrossRefGoogle Scholar
Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G., Nagel, S. R. & Witten, T. A. 1997 Capillary flow as the cause of ring stains from dried liquid drops. Nature 389, 827–829.CrossRefGoogle Scholar
Deegan, R. D., Bakajin, O., Dupont, T. F., Huber, G., Nagel, S. R. & Witten, T. A. 2000 Contact line deposits in an evaporating drop. Phys. Rev. E 62, 756–764.CrossRefGoogle Scholar
Derby, B. 2010 Inkjet printing of functional and structural materials: fluid property requirements, feature stability and resolution. Annu. Rev. Mater. Res. 40, 395–414.Google Scholar
Derby, B. & Reis, N. 2003 Inkjet printing of highly loaded particulate suspensions. MRS Bull. 28, 815–818.Google Scholar
Dong, H. & Carr, W. W. 2006 Visualization of drop-on-demand inkjet: drop formation and deposition. Rev. Sci. Instrum. 77, 085101.CrossRefGoogle Scholar
Dong, H., Carr, W. W. & Morris, J. F. 2006 An experimental study of drop-on-demand drop formation. Phys. Fluids 18, 072102.CrossRefGoogle Scholar
Duineveld, P. C. 2003 The stability of ink-jet printed lines of liquid with zero receding contact angle on a homogeneous substrate. J. Fluid Mech. 477, 175–200.Google Scholar
Duineveld, P. C., de Kok, M. M., Buechel, M., Sempel, A. H., Mutsaers, K. A. H., van de Weijer, P., Camps, I. G. J., van den Biggelaar, T. J. M., Rubingh, J. E. J. M. & Haskal, E. I. 2002 Ink-jet printing of polymer light-emitting devices. Proc. SPIE 4464, 59–67.Google Scholar
Fakhfouri, V., Mermoud, G., Kim, J. Y., Martinoli, A. & Brugger, J. 2009 Drop-on-demand inkjet printing of SU-8 polymer. Micro Nanosyst. 1, 63–67.Google Scholar
Fromm, J. E. 1984 Numerical calculations of the fluid dynamics of drop-on-demand jets. IBM J. Res. Dev. 28, 322–333.Google Scholar
Fuller, S. B., Wilhelm, E. J. & Jacobson, J. M. 2002 Ink-jet printed nanoparticle microelectromechanical systems. J. Microelectromech. Syst. 11, 54–60.Google Scholar
de Gans, B. J., Duineveld, P. C. & Schubert, U. S. 2004 Inkjet printing of polymers: state of the art and future developments. Adv. Mater. 16, 203–213.CrossRefGoogle Scholar
de Gans, B. J. & Schubert, U. S. 2004 Inkjet printing of well-defined polymer dots and arrays. Langmuir 20, 7789–7793.Google Scholar
Hoath, S. D., Hsiao, W.-K., Jung, S., Martin, G. D. & Hutchings, I. M. 2012 Drop speeds from drop-on-demand ink-jet print heads. J. Imaging Sci. Technol. (submitted).Google Scholar
Hoth, C. N., Schilinsky, P., Choulis, S. A. & Brabec, C. J. 2008 Printing highly efficient organic solar cells. Nano Lett. 8, 2806–2813.Google Scholar
Hu, H. & Larson, R. G. 2006 Maragoni effect reverses coffee-ring depositions. J. Phys. Chem. B 110, 7090–7094.Google Scholar
Hughes, T. R., Mao, M., Jones, A. R., Burchard, J., Marton, M. J., Shannon, K. W., Lefkowitz, S. M., Ziman, M., Schelter, J. M., Meyer, M. R., Kobayashi, S., Davis, C., Dai, H. Y., He, Y. D. D., Stephaniants, S. B., Cavet, G., Walker, W. L., West, A., Coffey, E., Shoemaker, D. D., Stoughton, R., Blanchard, A. P., Friend, S. H. & Linsley, P. S. 2001 Expression profiling using microarrays fabricated by an ink-jet oligonucleotide synthesizer. Nature Biotechnol. 19, 342–347.Google Scholar
Ikegawa, M. & Azuma, H. 2004 Droplet behaviours on substrates in thin-film formation using inkjet printing. JSME Intl J. B 47, 490–496.CrossRefGoogle Scholar
Jang, D., Kim, D. & Moon, J. 2009 Influence of fluid physical properties on inkjet printability. Langmuir 25, 2629–2635.Google Scholar
Kawase, T., Shimoda, T., Newsome, C., Sirringhaus, H. & Friend, R. H. 2003 Inkjet printing of polymer thin film transistors. Thin Solid Films 438–439, 279–287.Google Scholar
Kobayashi, H., Kanbe, S., Seki, S., Kigchi, H., Kimura, M., Yudasaka, I., Miyashita, S., Shimoda, T., Towns, C. R., Burroughes, J. H. & Friend, R. H. 2000 A novel RGB multicolor light-emitting polymer display. Synth. Metals 111, 125–128.CrossRefGoogle Scholar
Kumar, S. & Kruth, J. P. 2010 Composites by rapid prototyping technology. Mater. Design 31, 850–856.Google Scholar
Le Clair, B. P. & Hamielec, A. E. 1969 A numerical study of the drag on a sphere at low and intermediate Reynolds numbers. J. Atmos. Sci. 27, 308–315.Google Scholar
Li, S. P., Newsome, C. J., Kugler, T., Ishida, M. & Inoue, S. 2007 Polymer thin film transistors with self-aligned gates fabricated using ink-jet printing. Appl. Phys. Lett. 90, 172103.Google Scholar
Martin, G. D., Hoath, S. D. & Hutchings, I. M. 2008 Inkjet printing – the physics of manipulating liquid jets and drops. J. Phys.: Conf. Ser. 105, 1–14.Google Scholar
Meier, H., Loffelmann, U., Mager, D., Smith, P. J. & Korvink, J. G. 2009 Inkjet printed, conductive $25~\lrm{\ensuremath{\mu}} \mathrm{m} $ wide silver tracks on unstructured polyimide. Phys. Status Solidi A 206, 1626–1630.Google Scholar
Mott, M., Song, J. H. & Evans, J. R. G. 1999 Microengineering of ceramics by direct ink-jet printing. J. Am. Ceram. Soc. 82, 1653–1658.Google Scholar
Nakamura, M., Kobayashi, A., Takagi, F., Watanabe, A., Hiruma, Y., Ohuchi, K., Iwasaki, Y., Horie, M., Morita, I. & Takatani, S. 2005 Biocompatible inkjet printing technique for designed seeding of individual living cells. Tissue Eng. 11, 1658–1666.Google Scholar
Newman, J. D., Turner, A. P. F. & Marrazza, G. 1992 Ink-jet printing for the fabrication of amperometric glucose biosensors. Anal. Chim. Acta 262, 13–17.Google Scholar
Noguera, R., Lejeune, M. & Chartier, T. 2005 3D fine scale ceramic components formed by ink-jet prototyping process. J. Eur. Ceram. Soc. 25, 2055–2059.Google Scholar
Notz, P. K. & Basaran, O. A. 2006 Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256.Google Scholar
Osch, T. H. J., Perelaer, J., Laat, A. W. M. & Schubert, U. S. 2008 Inkjet printing of narrow conductive tracks on untreated polymeric substrates. Adv. Mater. 20, 343–345.Google Scholar
Perelaer, J., Smith, P. J., van den Bosch, E., van Grootel, S. S. C., Ketelaars, P. H. J. M. & Schubert, U. S. 2009 The spreading of inkjet-printed droplets with varying polymer molar mass on a dry solid substrate. Macromol. Chem. Phys. 210, 495–502.Google Scholar
Reis, N., Ainsley, C. & Derby, B. 2005 Ink-jet delivery of particle suspensions by piezoelectric droplet ejectors. J. Appl. Phys. 97, 094903.Google Scholar
Reis, N. & Derby, B. 2000 Ink jet deposition of ceramic suspensions: modeling and experiments of droplet formation. MRS Symp. Proc. 625, 117–122.CrossRefGoogle Scholar
Roth, E. A., Xu, T., Das, M., Gregory, C., Hickman, J. J. & Boland, T. 2004 Inkjet printing for high-throughput cell patterning. Biomaterials 25, 3707–3715.Google Scholar
Sachs, E., Cima, M., Williams, P., Brancazio, D. & Cornie, J. 1992 Three-dimensional printing: rapid tooling and prototypes directly from a CAD model. Trans. ASME: J. Engng Ind. 114, 481–488.Google Scholar
Schiaffino, S. & Sonin, A. A. 1997a Formation and stability of liquid and molten beads on a solid surface. J. Fluid Mech. 343, 95–110.Google Scholar
Schiaffino, S. & Sonin, A. A. 1997b Molten droplet deposition and solidification at low Weber numbers. Phys. Fluids 9, 3172–3187.CrossRefGoogle Scholar
Shield, T. W., Bogy, D. B. & Talke, F. E. 1987 Drop formation by DOD inkjet nozzles: a comparison of experiment and numerical simulation. IBM J. Res. Dev. 31, 96.Google Scholar
Singh, M., Haverinen, H. M., Dhagat, P. & Jabbour, G. E. 2009 Inkjet printing-process and its applications. Adv. Mater. 22, 673–685.CrossRefGoogle Scholar
Sirringhaus, H., Kawase, T., Friend, R. H., Shimoda, T., Inbasekaran, M., Wu, W. & Woo, E. P. 2000 High-resolution inkjet printing of all-polymer transistor circuits. Science 290, 2123–2126.CrossRefGoogle ScholarPubMed
Sivaramakrishnan, S., Chia, P. J., Yeo, Y. C., Chua, L. L. & Ho, P. K. H. 2007 Controlled insulator-to-metal transformation in printable polymer composites with nanometal clusters. Nature Mater. 6, 149–155.CrossRefGoogle ScholarPubMed
Soltman, D. & Subramanian, V. 2008 Inkjet-printed line morphologies and temperature control of the coffee ring effect. Langmuir 24, 2224–2231.Google Scholar
Son, Y., Kim, C., Yang, D. H. & Ahn, D. J. 2008 Spreading of an inkjet droplet on a solid surface with a controlled contact angle at low Weber and Reynolds numbers. Langmuir 24, 2900–2907.Google Scholar
Wijshoff, H. 2010 The dynamics of the piezo inkjet printhead operation. Phys. Rep. 491, 77–177.Google Scholar
Wong, L. Y., Png, R. Q., Silva, F. B. S., Chua, L. L., Repaka, D. V. M., Chen, S., Gao, X. Y., Ke, L., Chua, S. J., Wee, A. T. S. & Ho, P. K. H. 2010 Interplay of processing, morphological order, and charge-carrier mobility in polythiophene thin films deposited by different methods: comparison of spin-cast, drop-cast, and inkjet-printed films. Langmuir 26, 15494–15507.Google Scholar
Xia, Y. & Friend, R. H. 2006 Polymer bilayer structure via inkjet printing. Appl. Phys. Lett. 88, 163508.Google Scholar
Xu, Q. & Basaran, O. A. 2007 Computational analysis of drop-on-demand drop formation. Phys. Fluids 19, 102111.CrossRefGoogle Scholar
Xue, F., Liu, Z., Su, Y. & Varahramyan, K. 2006 Inkjet printed silver source/drain electrodes for low-cost polymer thin films transistors. Microelectron. Engng 83, 298–302.Google Scholar