Article contents
Isotropically active colloids under uniform force fields: from forced to spontaneous motion
Published online by Cambridge University Press: 14 April 2021
Abstract
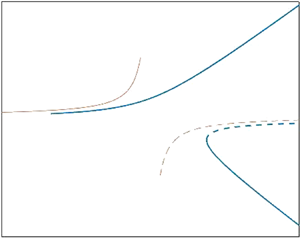
We consider the inertia-free motion of an isotropic chemically active particle which is exposed to a weak uniform force field. This problem is characterised by two velocity scales, a ‘chemical’ scale associated with diffusio-osmosis and a ‘mechanical’ scale associated with the external force. The motion animated by the force deforms the originally spherically symmetric solute cloud surrounding the particle, thus resulting in a concomitant diffusio-osmotic flow which, in turn, modifies the particle speed. A weak-force linearisation furnishes a closed-form expression for the particle velocity as a function of the intrinsic Péclet number  $\alpha$ associated with the chemical velocity scale. We find that the predicted velocity may become singular at
$\alpha$ associated with the chemical velocity scale. We find that the predicted velocity may become singular at  $\alpha =4$, and that this happens under the same conditions on the surface parameters for which the associated unforced problem is known to exhibit, for
$\alpha =4$, and that this happens under the same conditions on the surface parameters for which the associated unforced problem is known to exhibit, for  $\alpha >4$, a symmetry-breaking instability giving rise to steady spontaneous motion (Michelin, Lauga & Bartolo, Phys. Fluids, vol. 25, 2013, 061701). Here, a local analysis in a distinguished region near
$\alpha >4$, a symmetry-breaking instability giving rise to steady spontaneous motion (Michelin, Lauga & Bartolo, Phys. Fluids, vol. 25, 2013, 061701). Here, a local analysis in a distinguished region near  $\alpha =4$, wherein the velocity scaling is amplified, yields a closed-form description of the imperfect bifurcation which bridges between a perturbed stationary state and a perturbed spontaneous motion. Remarkably, while the direction of spontaneous motion in the absence of an external force is random, in the perturbed case that motion is rendered steady solely in the directions parallel or antiparallel to the external force.
$\alpha =4$, wherein the velocity scaling is amplified, yields a closed-form description of the imperfect bifurcation which bridges between a perturbed stationary state and a perturbed spontaneous motion. Remarkably, while the direction of spontaneous motion in the absence of an external force is random, in the perturbed case that motion is rendered steady solely in the directions parallel or antiparallel to the external force.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 18
- Cited by


