Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Goluskin, David
2016.
Internally Heated Convection and Rayleigh-Bénard Convection.
p.
27.
Goluskin, David
and
Doering, Charles R.
2016.
Bounds for convection between rough boundaries.
Journal of Fluid Mechanics,
Vol. 804,
Issue. ,
p.
370.
Mahajan, Amit
Ram, Paras
and
Makinde, Oluwole Daniel
2018.
Penetrative Internally Heated Convection in Magnetic Fluids.
Defect and Diffusion Forum,
Vol. 387,
Issue. ,
p.
373.
Ashour, Rakan F.
Kelley, Douglas H.
Salas, Alejandro
Starace, Marco
Weber, Norbert
and
Weier, Tom
2018.
Competing forces in liquid metal electrodes and batteries.
Journal of Power Sources,
Vol. 378,
Issue. ,
p.
301.
Bouillaut, Vincent
Lepot, Simon
Aumaître, Sébastien
and
Gallet, Basile
2019.
Transition to the ultimate regime in a radiatively driven convection experiment.
Journal of Fluid Mechanics,
Vol. 861,
Issue. ,
Miquel, Benjamin
Bouillaut, Vincent
Aumaître, Sébastien
and
Gallet, Basile
2020.
On the role of the Prandtl number in convection driven by heat sources and sinks.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Kumar, Anuj
and
Garaud, Pascale
2020.
Bound on the drag coefficient for a flat plate in a uniform flow.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Kumar, Anuj
2020.
Pressure-driven flows in helical pipes: bounds on flow rate and friction factor.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2021.
Bounds for internally heated convection with fixed boundary heat flux.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2021.
Bounds on heat transport for convection driven by internal heating.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
Tobasco, Ian
2022.
Optimal cooling of an internally heated disc.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2225,
Huang, Maojing
Wang, Yin
Bao, Yun
and
He, Xiaozhou
2022.
Heat transport and temperature boundary-layer profiles in closed turbulent Rayleigh–Bénard convection with slippery conducting surfaces.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Kumar, Anuj
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2022.
Analytical bounds on the heat transport in internally heated convection.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Huang, Maojing
and
He, Xiaozhou
2022.
Heat transport in horizontally periodic and confined Rayleigh-Bénard convection with no-slip and free-slip plates.
Theoretical and Applied Mechanics Letters,
Vol. 12,
Issue. 2,
p.
100330.
Fantuzzi, Giovanni
Arslan, Ali
and
Wynn, Andrew
2022.
The background method: theory and computations.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2225,
Song, Binglin
Fantuzzi, Giovanni
and
Tobasco, Ian
2023.
Bounds on heat transfer by incompressible flows between balanced sources and sinks.
Physica D: Nonlinear Phenomena,
Vol. 444,
Issue. ,
p.
133591.
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2023.
Rigorous scaling laws for internally heated convection at infinite Prandtl number.
Journal of Mathematical Physics,
Vol. 64,
Issue. 2,
Földes, Juraj
Glatt-Holtz, Nathan E.
Richards, Geordie
and
Whitehead, Jared P.
2024.
Hydrodynamic stability in the presence of a stochastic forcing: A case study in convection.
Physica D: Nonlinear Phenomena,
Vol. 465,
Issue. ,
p.
134196.
Agasthya, Lokahith
and
Muller, Caroline Jane
2024.
Dynamics and scaling of internally cooled convection.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 134,
Issue. ,
p.
108011.
Arslan, Ali
Fantuzzi, Giovanni
Craske, John
and
Wynn, Andrew
2024.
Internal heating profiles for which downward conduction is impossible.
Journal of Fluid Mechanics,
Vol. 993,
Issue. ,
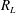 $R_{L}$ ), and the energy analysis yields a Rayleigh number below which it is globally stable (
$R_{L}$ ), and the energy analysis yields a Rayleigh number below which it is globally stable ( 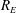 $R_{E}$ ). For various boundary conditions on the velocity, exact expressions for
$R_{E}$ ). For various boundary conditions on the velocity, exact expressions for 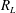 $R_{L}$ and
$R_{L}$ and 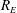 $R_{E}$ are found using long-wavelength asymptotics. Each
$R_{E}$ are found using long-wavelength asymptotics. Each  $R_{E}$ is strictly smaller than the corresponding
$R_{E}$ is strictly smaller than the corresponding 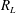 $R_{L}$ but is within 1 %. The lower bound on the mean temperature is proven for no-slip velocity boundary conditions using the background method. The bound guarantees that the mean temperature of the fluid, relative to that of the top boundary, grows with the heating rate (
$R_{L}$ but is within 1 %. The lower bound on the mean temperature is proven for no-slip velocity boundary conditions using the background method. The bound guarantees that the mean temperature of the fluid, relative to that of the top boundary, grows with the heating rate ( 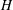 $H$ ) no slower than
$H$ ) no slower than 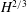 $H^{2/3}$ .
$H^{2/3}$ .

