Article contents
Internal wave focusing by a horizontally oscillating torus
Published online by Cambridge University Press: 26 January 2017
Abstract
This paper presents an experimental study on internal waves emitted by a horizontally oscillating torus in a linearly stratified fluid. Two internal wave cones are generated with the kinetic energy focused at the apices of the cones above and below the torus where the wave amplitude is maximal. Their motion is measured via tracking of distortions of horizontal fluorescein dye planes created prior to the experiments and illuminated by a vertical laser sheet. The distortion of the dye planes gives a direct access to the Lagrangian displacement of local wave amplitudes and slopes, and in particular, allows us to calculate a local Richardson number. In addition particle image velocimetry measurements are used. Maximum wave slopes are found in the focal region and close to the surface of the torus. As the amplitude of oscillations of the torus increases, wave profiles in the regions of maximum wave slopes evolve nonlinearly toward local overturning. A theoretical approximation based on the theory of Hurley & Keady (J. Fluid Mech., vol. 351, 1997, pp. 119–138) is presented and shows, for small amplitudes of oscillation, a very reasonable agreement with the experimental data. For the focal region the internal wave amplitude is found to be overestimated by the theory. The wave breaking in the focal region is investigated as a function of the Keulegan–Carpenter number,  $Ke=A/a$ , with
$Ke=A/a$ , with 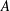 $A$ the oscillation amplitude and
$A$ the oscillation amplitude and  $a$ the short radius of the torus. A linear wave regime is found for
$a$ the short radius of the torus. A linear wave regime is found for 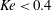 $Ke<0.4$ , nonlinear effects start at
$Ke<0.4$ , nonlinear effects start at 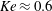 $Ke\approx 0.6$ and breaking for
$Ke\approx 0.6$ and breaking for 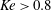 $Ke>0.8$ . For large forcing, the measured wave amplitude normalized with the oscillation amplitude decreases almost everywhere in the wave field, but increases locally in the focal region due to nonlinear effects. Due to geometric focusing the amplitude of the wave increases with
$Ke>0.8$ . For large forcing, the measured wave amplitude normalized with the oscillation amplitude decreases almost everywhere in the wave field, but increases locally in the focal region due to nonlinear effects. Due to geometric focusing the amplitude of the wave increases with 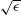 $\sqrt{\unicode[STIX]{x1D716}}$ , with
$\sqrt{\unicode[STIX]{x1D716}}$ , with 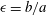 $\unicode[STIX]{x1D716}=b/a$ and
$\unicode[STIX]{x1D716}=b/a$ and 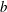 $b$ is the mean radius of the torus. The relevance of wave focusing due to ocean topography is discussed.
$b$ is the mean radius of the torus. The relevance of wave focusing due to ocean topography is discussed.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 13
- Cited by


