No CrossRef data available.
Article contents
The instability of non-monotonic drag laws
Published online by Cambridge University Press: 13 September 2024
Abstract
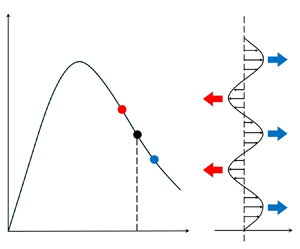
A series of recent studies has indicated that the component of the bottom drag caused by irregular small-scale topography in the ocean varies non-monotonically with the flow speed. The roughness-induced forcing increases with the speed of relatively slow abyssal currents but, somewhat counterintuitively, starts to decrease when flows are sufficiently swift. This reduction in drag at high speeds leads to the instability of laterally uniform currents, and the resulting evolutionary patterns are explored using numerical and analytical methods. The drag-law instability manifests in the spontaneous emergence of parallel jets, aligned in the direction of the basic flow and separated by relatively quiescent regions. We hypothesize that the mechanisms identified in this investigation could play a role in the dynamics of zonal striations commonly observed in the ocean.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


