Article contents
Instability and transition of a vertical ascension or fall of a free sphere affected by a vertical magnetic field
Published online by Cambridge University Press: 16 November 2018
Abstract
When the Galileo number is below the first bifurcation, the instability and transition of a vertical ascension or the fall of a free sphere affected by a vertical magnetic field are investigated numerically. A compact model is used to explain that the magnetic field can destabilize the fluid–solid system. When the interaction parameter exceeds a critical value, the sphere trajectory is transitioned from a steady vertical trajectory to a steady oblique one. Furthermore, the trajectory will remain vertical at a sufficiently large magnetic field because of a double effect of the magnetic field on the fluid–solid system. Under the influence of an external vertical magnetic field, four wake patterns at the rear of the sphere are found and the physical behaviour of the free sphere is independent of the density ratio. The wake or trajectory of the free sphere is only determined by the Galileo number 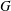 $G$ and the interaction parameter
$G$ and the interaction parameter 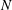 $N$. A close relationship between the streamwise vorticity and the sphere motion is found. An interesting ‘agglomeration phenomenon’ is also found, which shows that the vertical velocities are agglomerated into a point for a certain magnetic field regardless of the Galileo number and satisfy a scaling law
$N$. A close relationship between the streamwise vorticity and the sphere motion is found. An interesting ‘agglomeration phenomenon’ is also found, which shows that the vertical velocities are agglomerated into a point for a certain magnetic field regardless of the Galileo number and satisfy a scaling law 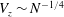 $V_{z}\sim N^{-1/4}$, when
$V_{z}\sim N^{-1/4}$, when  $N>1$. The principal results of the present work are summarized in a map of regimes in the
$N>1$. The principal results of the present work are summarized in a map of regimes in the 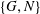 $\{G,N\}$ plane.
$\{G,N\}$ plane.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 10
- Cited by

