Article contents
Insights into the dynamics of conical breakdown modes in coaxial swirling flow field
Published online by Cambridge University Press: 22 August 2018
Abstract
The main idea of this paper is to understand the fundamental vortex breakdown mechanisms in the coaxial swirling flow field. In particular, the interaction dynamics of the flow field is meticulously addressed with the help of high fidelity laser diagnostic tools. Time-resolved particle image velocimetry (PIV) (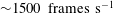 ${\sim}1500~\text{frames}~\text{s}^{-1}$) is employed in
${\sim}1500~\text{frames}~\text{s}^{-1}$) is employed in 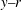 $y{-}r$ and multiple
$y{-}r$ and multiple 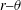 $r{-}\unicode[STIX]{x1D703}$ planes to precisely delineate the flow dynamics. Experiments are carried out for three sets of co-annular flow Reynolds number
$r{-}\unicode[STIX]{x1D703}$ planes to precisely delineate the flow dynamics. Experiments are carried out for three sets of co-annular flow Reynolds number 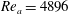 $Re_{a}=4896$, 10 545, 17 546. Furthermore, for each
$Re_{a}=4896$, 10 545, 17 546. Furthermore, for each 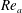 $Re_{a}$ condition, the swirl number ‘
$Re_{a}$ condition, the swirl number ‘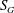 $S_{G}$’ is varied independently from
$S_{G}$’ is varied independently from 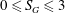 $0\leqslant S_{G}\leqslant 3$. The global evolution of flow field across various swirl numbers is presented using the time-averaged PIV data. Three distinct forms of vortex breakdown namely, pre-vortex breakdown (PVB), central toroidal recirculation zone (CTRZ; axisymmetric toroidal bubble type breakdown) and sudden conical breakdown are witnessed. Among these, the conical form of vortex breakdown is less explored in the literature. In this paper, much attention is therefore focused on exploring the governing mechanism of conical breakdown. It is should be interesting to note that, unlike other vortex breakdown modes, conical breakdown persists only for a very short band of
$0\leqslant S_{G}\leqslant 3$. The global evolution of flow field across various swirl numbers is presented using the time-averaged PIV data. Three distinct forms of vortex breakdown namely, pre-vortex breakdown (PVB), central toroidal recirculation zone (CTRZ; axisymmetric toroidal bubble type breakdown) and sudden conical breakdown are witnessed. Among these, the conical form of vortex breakdown is less explored in the literature. In this paper, much attention is therefore focused on exploring the governing mechanism of conical breakdown. It is should be interesting to note that, unlike other vortex breakdown modes, conical breakdown persists only for a very short band of 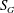 $S_{G}$. For any small increase/decrease in
$S_{G}$. For any small increase/decrease in 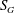 $S_{G}$ beyond a certain threshold, the flow spontaneously reverts back to the CTRZ state. Energy ranked and frequency-resolved/ranked robust structure identification methods – proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD) respectively – are implemented over instantaneous time-resolved PIV data sets to extract the dynamics of the coherent structures associated with each vortex breakdown mode. The dominant structures obtained from POD analysis suggest the dominance of the Kelvin–Helmholtz (KH) instability (axial
$S_{G}$ beyond a certain threshold, the flow spontaneously reverts back to the CTRZ state. Energy ranked and frequency-resolved/ranked robust structure identification methods – proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD) respectively – are implemented over instantaneous time-resolved PIV data sets to extract the dynamics of the coherent structures associated with each vortex breakdown mode. The dominant structures obtained from POD analysis suggest the dominance of the Kelvin–Helmholtz (KH) instability (axial 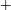 $+$ azimuthal; accounts for
$+$ azimuthal; accounts for 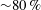 ${\sim}80\,\%$ of total turbulent kinetic energy, TKE) for both PVB and CTRZ while the remaining energy is contributed by shedding modes. On the other hand, shedding modes contribute the majority of the TKE in conical breakdown. The frequency signatures quantified from POD temporal modes and DMD analysis reveal the occurrence of multiple dominant frequencies in the range of
${\sim}80\,\%$ of total turbulent kinetic energy, TKE) for both PVB and CTRZ while the remaining energy is contributed by shedding modes. On the other hand, shedding modes contribute the majority of the TKE in conical breakdown. The frequency signatures quantified from POD temporal modes and DMD analysis reveal the occurrence of multiple dominant frequencies in the range of 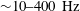 ${\sim}10{-}400~\text{Hz}$ with conical breakdown. This phenomenon may be a manifestation of high energy contribution by shedding eddies in the shear layer. Contrarily, with PVB and CTRZ, the dominant frequencies are observed in the range of
${\sim}10{-}400~\text{Hz}$ with conical breakdown. This phenomenon may be a manifestation of high energy contribution by shedding eddies in the shear layer. Contrarily, with PVB and CTRZ, the dominant frequencies are observed in the range of 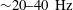 ${\sim}20{-}40~\text{Hz}$ only. We have provided a detailed exposition of the mechanism through which conical breakdown occurs. In addition, the current work explores the hysteresis (path dependence) phenomena of conical breakdown as functions of the Reynolds and Rossby numbers. It has been observed that the conical mode is not reversible and highly dependent on the initial conditions.
${\sim}20{-}40~\text{Hz}$ only. We have provided a detailed exposition of the mechanism through which conical breakdown occurs. In addition, the current work explores the hysteresis (path dependence) phenomena of conical breakdown as functions of the Reynolds and Rossby numbers. It has been observed that the conical mode is not reversible and highly dependent on the initial conditions.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 21
- Cited by

