Article contents
Inner–outer interactions of large-scale structures in turbulent channel flow
Published online by Cambridge University Press: 02 February 2016
Abstract
Direct numerical simulation data of turbulent channel flow ( 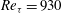 $Re_{{\it\tau}}=930$ ) are used to investigate the statistics of long motions of streamwise velocity fluctuations (
$Re_{{\it\tau}}=930$ ) are used to investigate the statistics of long motions of streamwise velocity fluctuations (  $u$ ), and the interaction of these structures with the near-wall disturbances, which is facilitated by their associated large-scale circulations. In the log layer, the negative-
$u$ ), and the interaction of these structures with the near-wall disturbances, which is facilitated by their associated large-scale circulations. In the log layer, the negative-  $u$ structures are organized into longer streamwise extent (
$u$ structures are organized into longer streamwise extent ( 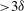 ${>}3{\it\delta}$ ) in comparison to the positive-
${>}3{\it\delta}$ ) in comparison to the positive-  $u$ counterparts. Near the wall, the footprint of negative-
$u$ counterparts. Near the wall, the footprint of negative-  $u$ structures is relatively narrow in comparison to the footprint of positive-
$u$ structures is relatively narrow in comparison to the footprint of positive-  $u$ structures. This difference is due to the opposite spanwise motions in the vicinity of the footprints, which are either congregative or dispersive depending on the circulation of the outer roll cells. Conditional sampling of the footprints shows that the spanwise velocity fluctuations (
$u$ structures. This difference is due to the opposite spanwise motions in the vicinity of the footprints, which are either congregative or dispersive depending on the circulation of the outer roll cells. Conditional sampling of the footprints shows that the spanwise velocity fluctuations ( 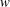 $w$ ) are significantly enhanced by the dispersive motions of high-speed structures. On the other hand, the near-wall congregative motions of negative-
$w$ ) are significantly enhanced by the dispersive motions of high-speed structures. On the other hand, the near-wall congregative motions of negative-  $u$ structures generate relatively weak
$u$ structures generate relatively weak 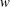 $w$ but intense negative-
$w$ but intense negative-  $u$ regions due, in part, to the spanwise collective migration of near-wall streaks. The concentrated near-wall regions of negative-
$u$ regions due, in part, to the spanwise collective migration of near-wall streaks. The concentrated near-wall regions of negative-  $u$ upwell during the merging of the outer long scales – an effect that is demonstrated using statistical analysis of the merging process. This leads to a reduction of the convection speed of downstream negative-
$u$ upwell during the merging of the outer long scales – an effect that is demonstrated using statistical analysis of the merging process. This leads to a reduction of the convection speed of downstream negative-  $u$ structures and thus promotes the merging with upstream ones. These top-down and bottom-up interactions enhance the spatial coherence of long negative-
$u$ structures and thus promotes the merging with upstream ones. These top-down and bottom-up interactions enhance the spatial coherence of long negative-  $u$ structures in the log region.
$u$ structures in the log region.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 86
- Cited by


